



Next: List of Tables
Up: compil
Previous: Création de paires et
Contents
- Invention en ut majeur, Johann Sebastian Bach, BWV 772, 1722
- Schéma de base des AGN (Urry & Padovani, Copyright 1995:
Astronomical Society of the Pacific, reproduit avec autorisation).
- Définition de l'angle d'observation.
- Mouvement superluminal [9].
- a): Pourcentage d'AGN détectés dans une bande de fréquence
donnée en fonction de la fréquence pour tous les objets (trait plein), pour
les émetteurs radio intenses (tirets) et pour les émetteurs radio faibles
(pointillés). b): Sensibilité des instruments à très grand champ en fonction
de la fréquence. Source: P. Padovani [16].
- Image schématique d'une cascade atmosphérique.
- Comparaison des principales expériences et projets d'astronomie
gamma.
- Site de Thémis. Les grands miroirs plans sont en cours de
réutilisation par l'expérience CELESTE. On distingue les larges paraboles
d'ASGAT et les petits télescopes Themistocle. L'imageur CAT a été
construit au centre du champ, entre les abris Themistocle et
ASGAT.
- Positions relatives des différentes expériences sur le site de Thémis.
- Une des voies d'acquisition de l'expérience Thémistocle.
- Distribution de (E-Ê)/E montrant une résolution statistique de
10%.
- Télescope au coucher du Soleil...
- Principe du miroir de l'imageur CAT.
- Support des miroirs du télescope. Figure LPNHE-X.
- Réflectivité des miroirs.
- Pixels (constitués de photomultiplicateurs) dans le plan focal du
télescope.
- Efficacité quantique de la photocathode [43].
- Piedestal et spectre du photoélectron avec un gain de
 .
.
- Distribution des rapports
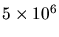 pour 225 photomultiplicateurs
testés.
pour 225 photomultiplicateurs
testés.
- Impulsion mesurée d'un photomultiplicateur R3678.
- Taux de comptage du photomultiplicateur éclairé en lumière aléatoire
en fonction du seuil de discrimination.
- Distribution des tensions à gain
donné.
- Aire des impulsions (charge) en fonction de l'amplitude.
- Piedestal et spectre du photoélectron avec un gain de
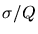 pour les photomultiplicateurs de garde. Le pic à deux photoélectrons est
également visible.
pour les photomultiplicateurs de garde. Le pic à deux photoélectrons est
également visible.
- Concentration de la lumière par un cône de Winston (partie
supérieure) sur un photomultiplicateur (partie inférieure). Figure LPNHE-X.
- Efficacité des cônes en fonction de l'angle d'incidence de la
lumière.
- Montage utilisé pour la caractérisation des cônes.
- Réflectivité effective des trois cônes testés.
- Effet des cônes sur la lumière Tcherenkov. La courbe en
pointillés
donne le spectre d'émission de la lumière Tcherenkov (divisé par 4 pour la
lisibilité), la courbe en tirets est le résultat de la multiplication
par l'efficacité quantique de la photocathode et la courbe
en trait plein est identique à la précédente après ajout de l'effet des
cônes. L'ensemble est représenté à différentes altitutes d'émission
(de 0 à 16 km) et il apparaît que la fraction de lumière perdue par les
cônes demeure constante.
- Impulsion mesurée d'un photomultiplicateur R3878
après l'amplificateur OPA 623.
- Zones de déclenchement, avec secteurs et sous-secteurs (ou secteurs
élémentaires).
- Impulsion mesurée d'un photomultiplicateur R3878
après l'amplificateur NEC 1678.
- Principe de traitement d'une des 288 voies électroniques participant au
déclenchement.
- Architecture de l'électronique de l'imageur.
- Synoptique de l'électronique de l'imageur.
- Répartition temporelle des différents éléments.
- Banc test développé au LPNHE-Paris pour étalonner la réponse de
l'électronique de l'imageur.
- Mesure à l'aide d'un générateur d'impulsions rapides de la
réponse des voies analogiques.
- Dispersion entre les différentes voies du système d'acquisition.
- Nombre de photoélectrons mesurés dans une voie en fonction du nombre de
photoélectrons "injectés" dans la voie voisine.
- Nombre de canaux d'ADC mesurés en fonction de la largeur de la porte
analogique rapide pour 4 voies électroniques différentes.
- Distribution des facteurs de conversion (canaux ADC /
photoélectron).
- Historique de la valeur moyenne des facteurs de conversion. Le saut à la
11
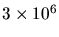 marche vient d'un réajustement des hautes tensions. Chaque pas
correspond à une mesure LED.
marche vient d'un réajustement des hautes tensions. Chaque pas
correspond à une mesure LED.
- Histogramme de charge d'une voie typique d'ADC.
- Gauche: histogramme de charge des événements logiciels d'une voie ADC avec la
fonction
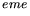 ajustée en trait plein. Droite: distribution du bruit mesuré en
photoélectrons par nanoseconde dans l'ensemble de la caméra et simple gaussienne pour
évaluer la moyenne.
ajustée en trait plein. Droite: distribution du bruit mesuré en
photoélectrons par nanoseconde dans l'ensemble de la caméra et simple gaussienne pour
évaluer la moyenne.
- Histogramme des largeurs de piedestaux, en canaux ADC,
sur les 546 voies internes moyennées sur un an.
- Gauche: évolution de la position du piedestal, en canaux ADC, de la voie 34 (typique)
depuis le début du fonctionnement du télescope. Droite: même distribution pour
la largeur du piedestal.
- Dispersion de charge brute en photoélectrons.
- Charge en fonction du rayon séparant le pixel du centre de la
caméra.
- Dispersion de charge, en photoélectrons, corrigée de l'effet de la
LED.
- De gauche à droite. Spectres pour a): photomultiplicateur de gain moyen (12.4 cx/
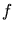 ) et de bonne
efficacité optique (13%) b): photomultiplicateur de gain faible (8.5 cx/
) et de bonne
efficacité optique (13%) b): photomultiplicateur de gain faible (8.5 cx/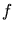 ) et de bonne
efficacité optique (9%) c): photomultiplicateur de gain élevé (13.1 cx/
) et de bonne
efficacité optique (9%) c): photomultiplicateur de gain élevé (13.1 cx/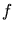 ) et de
faible efficacité optique.
) et de
faible efficacité optique.
- a): Facteurs de correction avec diaphragme en fonction des facteurs de
correction sans diaphragme b): Facteurs de correction des efficacités
quantiques en fonction des
facteurs de correction LED (sans diaphragme) c): Facteurs de correction
aléatoires en fonction des facteurs de correction
réels d): Facteurs de correction sur événements réels en fonction des
facteurs de correction déterminés avec la LED. Pour chaque figure le trait
plein indique la distribution idéale y=x.
- facteurs de correction (acquisitions LED avec diaphragme) avec les anciennes tensions en
fonction des facteurs avec les nouvelles tensions.
- Distribution des facteurs de correction optiques pour l'ensemble des
photomultiplicateurs.
- Corrections mécaniques estimées à partir des acquisitions transits:
distribution et modélisation des décalages
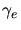 en fonction de l'azimut.
en fonction de l'azimut.
- Position des caméras CCD sur le télescope. Les pièces
numérotées représentent (1): le support du miroir, (2): les connexions, (3):
le support global, (4): la caméra de photomultiplicateurs, (5): les baies
électroniques.
- Cascades induites par un photon gamma (gauche) et par un hadron
(droite) [62].
- Visualisation "simplifiée" de la formation de l'image elliptique
dans le plan focal de la caméra.
- Image d'un événement réel de type gamma visualisé dans CAT.
- Définition géométrique des paramètres de Hillas dans le cadre
d'une approximation elliptique de la forme de l'image. Le point C
représente le barycentre de l'image pondérée par la quantité de
lumière.
- Gauche: distribution des longueurs (
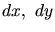 ) d'images de photons et de hadrons.
Droite: distribution des largeurs (
) d'images de photons et de hadrons.
Droite: distribution des largeurs (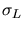 ) d'images de photons et de hadrons.
) d'images de photons et de hadrons.
- Angle de pointé
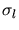 calculé sur la base des paramètres de Hillas
pour des gammas simulés au zénith à 100 GeV, 300 GeV, 1 TeV et 15 TeV.
calculé sur la base des paramètres de Hillas
pour des gammas simulés au zénith à 100 GeV, 300 GeV, 1 TeV et 15 TeV.
- Quantité de lumière en photoélectrons par centième de degré en
fonction de la distance longitudinale à la source, pour différents paramètres
d'impact. Les traits pleins réguliers et les pointillés correspondent au modèle
(avant et après discrétisation) et les traits pleins plus "chaotiques" aux
simulations.
- Valeur du
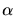 en échelle logarithmique pour deux
paramètres libres dans la minimisation: le paramètre d'impact et le
logarithme de l'énergie (à une constante multiplicative près).
en échelle logarithmique pour deux
paramètres libres dans la minimisation: le paramètre d'impact et le
logarithme de l'énergie (à une constante multiplicative près).
- Distribution de probabilité de
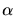 pour des gammas simulés à
600 GeV dont le paramètre d'impact est inférieur à 60 mètres (zone sensible
à la différence entre
pour des gammas simulés à
600 GeV dont le paramètre d'impact est inférieur à 60 mètres (zone sensible
à la différence entre 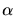 et
et 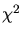 ). Partie
supérieure: avec le
). Partie
supérieure: avec le 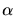 initial. Partie inférieure: avec
initial. Partie inférieure: avec 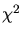 tenant
compte des variations de fluctuation avec
tenant
compte des variations de fluctuation avec 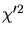 .
.
- Distribution de probabilité de
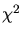 pour des gammas simulés et
des hadrons réels. Une coupure à 0.2, utilisée dans l'analyse, conserve 66%
des gammas et 20% des
hadrons, une coupure à 0.5 conserve 18% des gammas et 3% des hadrons.
pour des gammas simulés et
des hadrons réels. Une coupure à 0.2, utilisée dans l'analyse, conserve 66%
des gammas et 20% des
hadrons, une coupure à 0.5 conserve 18% des gammas et 3% des hadrons.
- Partie supérieure: différence entre les paramètres d'impact
estimés (avant minimisation de
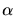 ) et réels, en mètres, pour des gammas simulés
à un angle zénithal de
) et réels, en mètres, pour des gammas simulés
à un angle zénithal de 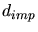 . Partie inférieure: différence entre
. Partie inférieure: différence entre 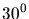 estimé (avant minimisation de
estimé (avant minimisation de 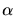 ) et
) et 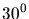 réel, pour
réel, pour
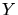 ,
sur le même lot de gammas.
,
sur le même lot de gammas.
- Nombre total de photoélectrons contenus dans une image en fonction du
paramètre d'impact pour différentes énergies de gammas au zénith.
- Nombre total de photoélectrons contenus dans une image en fonction du
paramètre d'impact pour différentes énergies de gammas à
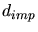 du zénith.
du zénith.
- Partie supérieure: distributions, pour des gammas simulés en loi de
puissance du Crabe, du nombre de "groupes de pixels" dans l'image et du nombre de
voies dans le plus grand groupe. Partie inférieure: mêmes distributions pour
des hadrons (données réelles "OFF-source").
- Partie supérieure: biais entre l'énergie reconstruite
et l'énergie réelle (logarithme du rapport) en fonction de l'énergie réelle.
Partie inférieure: écart-type, en mètres, de la gaussienne ajustée sur le logarithme du
rapport entre les énergies reconstruites et réelles en
fonction de l'énergie réelle.
- Partie supérieure: biais entre le paramètre d'impact reconstruit
et le paramètre d'impact réel en fonction de l'énergie réelle. Partie
inférieure: écart-type de la gaussienne ajustée sur la différence
des paramètres d'impact reconstruits et réels en
fonction de l'énergie réelle.
- Surface effective de détection en fonction de l'énergie pour
différents angles zénithaux. Les lignes représentent la fonction analytique
ajustée et les points les valeurs exactes venant de la simulation.
- Multiplication de la surface de détection par le flux
différentiel de la Nébuleuse du Crabe en fonction de l'énergie pour
différents angles zénithaux.
- Part des gammas simulés conservés par les coupures standard
en fonction de l'énergie.
- Distribution des intervalles de temps en
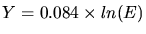 séparant deux
événements
enregistrés.
séparant deux
événements
enregistrés.
- Spectres d'ADC en canaux: la partie haute représente les données
réelles et la partie basse les simulations. La figure de gauche est relative aux
photomultiplicateurs intérieurs et celle de droite aux photomultiplicateurs
de garde.
- Comparaison entre les longueurs des images sur des gammas réels (en
traits pleins) obtenus lors d'un sursaut de Mrk501 par soustraction "ON-OFF" et
des gammas simulés (pointillés).
- Comparaison entre les largeurs des images sur des gammas réels (en
traits pleins) obtenus lors d'un sursaut de Mrk501 par soustraction "ON-OFF" et
des gammas simulés (pointillés).
- Comparaison entre les distributions de probabilité de
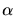 obtenues sur des gammas réels (en
traits pleins) lors d'un sursaut de Mrk501 par soustraction "ON-OFF" et
des gammas simulés (pointillés).
obtenues sur des gammas réels (en
traits pleins) lors d'un sursaut de Mrk501 par soustraction "ON-OFF" et
des gammas simulés (pointillés).
- Distribution des acquisitions dans le plan des
variables dislis / pente (pour un lot sélectionné) avec deux
méthodes
de calcul. Le rectangle inférieur gauche correspond à une météorologie
parfaite.
- Distribution des paramètres de sélection de données pour l'essentiel des
acquisitions.
- Fréquence (Hz) d'événements enregistrés en fonction de l'angle
zénithal d'observation (degrés).
- "lego-plot" des directions reconstruites d'arrivée des gammas du
Crabe en mode "ON"-"OFF" à partir des observations de janvier et février
1997.
- Spectre différentiel de la nébuleuse du Crabe.
- Distribution des fréquences d'événements enregistrés avec 10
héliostats en coïncidence.
- Partie supérieure: différence des énergies reconstruites par Themistocle et
CAT (en TeV) sur des événements communs de "type hadron". Partie inférieure:
différence des énergies reconstruites par Themistocle et CAT sur des événements
communs de "type gamma".
- Mêmes distributions qu'à la figure précédente pour le logarithme du rapport
des énergies.
- Image optique de Mrk501 (spectre visible) avec un champ de vue de 10'
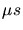 10',
obtenue par le groupe de Heidelberg-Königstuhl
(
10',
obtenue par le groupe de Heidelberg-Königstuhl
(
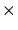 ) [83].
) [83].
- Histogramme de l'angle de pointé
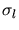 (défini au premier chapitre de la
partie précédente) durant la nuit du 15
avril 1997. Si l'on se restreint aux 9 premiers degrés, le rapport signal/bruit
exceptionnel permet de disposer d'un faisceau de gammas
faiblement contaminés en hadrons. L'encart supérieur donne la distribution de
(défini au premier chapitre de la
partie précédente) durant la nuit du 15
avril 1997. Si l'on se restreint aux 9 premiers degrés, le rapport signal/bruit
exceptionnel permet de disposer d'un faisceau de gammas
faiblement contaminés en hadrons. L'encart supérieur donne la distribution de
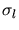 en mode "ON"-"OFF".
en mode "ON"-"OFF".
- Carte des directions reconstruites des gammas en provenance de Mrk501
en représentation "ON"-"OFF" dans les coordonnées de la caméra (mrad).
- Courbe de lumière de Mrk501 incluant toutes les données de CAT à
moins de
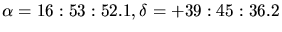 du zénith.
du zénith.
- Courbes de lumière comparées de CAT, Whipple et HEGRA obtenues sur
Mrk501 au mois d'avril.
- Flux différentiels de Mrk501 mesurés pendant le sursaut le plus
important, avec toutes les données (angle zénithal
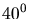 ) et hors des
sursauts.
) et hors des
sursauts.
- Valeurs du facteur de Lorentz
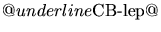 (en fonction du rayon du nodule) possibles compte-tenu de la double contrainte sur
le temps de variabilité et sur l'énergie maximum détectée.
(en fonction du rayon du nodule) possibles compte-tenu de la double contrainte sur
le temps de variabilité et sur l'énergie maximum détectée.
- Paramètres géométriques du modèle.
- Distance du nuage à l'AGN (en unités de
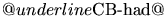 cm) en fonction de la masse du trou
noir (en unités de
cm) en fonction de la masse du trou
noir (en unités de 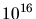 masses solaires) selon les résultats
de CAT, pour des rayons de nuage
masses solaires) selon les résultats
de CAT, pour des rayons de nuage 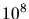 (en unités de
(en unités de 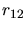 cm) de 1 et 100.
cm) de 1 et 100.
- Limite inférieure du champ magnétique H (en gauss) en fonction du
facteur Doppler
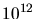 suivant les résultats CAT-XTE:
suivant les résultats CAT-XTE:
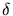 .
.
- Spectres prévus par le modèle E-PIC (cercles pour
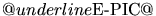 et croix pour
et croix pour 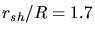 ) superposés
aux mesures de CAT (trait plein, normalisation arbitraire).
) superposés
aux mesures de CAT (trait plein, normalisation arbitraire).
- Angle du cône d'émission gamma en milliradians en fonction de la
distance entre l'étoile et le trou noir en parsecs selon les mesures de CAT.
- Modèle EC: géométrie de la source. Le nodule d'émission,
symbolisé par un cylindre de rayon
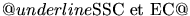 ,
se déplace le long du jet avec un facteur de Lorentz
,
se déplace le long du jet avec un facteur de Lorentz 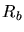 .
Le jet sous-jacent se déplace avec un facteur de Lorentz
.
Le jet sous-jacent se déplace avec un facteur de Lorentz
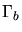 , éventuellement différent de
, éventuellement différent de 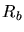 .
.
- Distribution spectrale théorique de l'énergie: émission synchrotron
présentant un palier jusqu'à
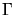 (avec présence d'une cassure à
(avec présence d'une cassure à 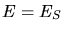 ),
émission Compton-inverse par le faisceau froid avec un maximum à
),
émission Compton-inverse par le faisceau froid avec un maximum à 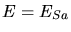 et
émission Compton-inverse par le faisceau chaud présentant un palier jusqu'à
et
émission Compton-inverse par le faisceau chaud présentant un palier jusqu'à 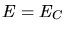 (avec présence d'une cassure à
(avec présence d'une cassure à 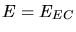 ).
L'énergie des photons-cible externes est
centrée sur
).
L'énergie des photons-cible externes est
centrée sur 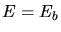 .
.
- Courbe de lumière obtenue à partir des données de XTE
(2-10 keV) et de CAT (0.3-15 TeV).
Les lignes pointillées séparent les zones correspondant à
l'état bas et à l'état haut; on appelle sursauts
les moments d'intense activité gamma.
- Histogrammes des mesures, moyennées par jour, de XTE en état bas (en haut) et en état haut (milieu)
et des mesures de CAT en état haut (en bas).
Les maxima estimés après ajustement d'une gaussienne sur
les données sont de 0.46
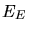 pour l'état bas et de 1.25
pour l'état bas et de 1.25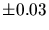 pour l'état haut en X, de 2.3
pour l'état haut en X, de 2.3 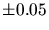 pour l'état haut en gamma.
pour l'état haut en gamma.
- Coefficient de corrélation entre les données de XTE et les
données de CAT en fonction du décalage en jours
des mesures en X par rapport aux mesures en gamma.
- Distribution spectrale de l'énergie en fonction de
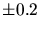 . Partie synchrotron:
le premier point, les
. Partie synchrotron:
le premier point, les 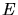 ,
, 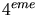 et
et 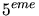 sont extraits de Sambruna et al,
le second vient de [195],
le
sont extraits de Sambruna et al,
le second vient de [195],
le 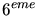 est issu de mesures faites à l'IRAM entre 1985 et 1992 (H. Ungerechts, communication privée).
La partie inverse Compton utilise les résultats de CAT. Les lignes pointillées
correspondent à l'ajustement d'une parabole.
La partie synchrotron en état haut est symboliquement représentée par les
segments en pointillés [194].
est issu de mesures faites à l'IRAM entre 1985 et 1992 (H. Ungerechts, communication privée).
La partie inverse Compton utilise les résultats de CAT. Les lignes pointillées
correspondent à l'ajustement d'une parabole.
La partie synchrotron en état haut est symboliquement représentée par les
segments en pointillés [194].
- Distribution spectrale de l'énergie en fonction de
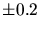 .
Figure extraite de [122], contenant notamment l'ensemble des mesures obtenues par le satellite
BeppoSax.
Afin de comparer l'échelle verticale
de cette figure avec celle de la figure 12.12, 1 erg cm
.
Figure extraite de [122], contenant notamment l'ensemble des mesures obtenues par le satellite
BeppoSax.
Afin de comparer l'échelle verticale
de cette figure avec celle de la figure 12.12, 1 erg cm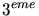 s
s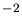 = 10
= 10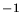 J m
J m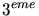 s
s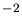 .
.
- Valeurs du facteur de Lorentz
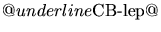 (en haut) et de l'intensité du
champ magnétique
(en haut) et de l'intensité du
champ magnétique 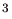 (en bas) en fonction de la
fréquence des photons cible. Les flèches indiquent les mesures extrêmes
considérées pour la fréquence des photons
synchrotron (état bas et état haut) ou externe (Lyman
(en bas) en fonction de la
fréquence des photons cible. Les flèches indiquent les mesures extrêmes
considérées pour la fréquence des photons
synchrotron (état bas et état haut) ou externe (Lyman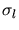 ou plasma chaud).
ou plasma chaud).
- Valeur du rayon de la zone émettrice
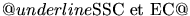 en fonction de la fraction de la zone participant à
l'émission gamma,
en fonction de la fraction de la zone participant à
l'émission gamma, 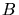 , et du facteur de Lorentz du jet
, et du facteur de Lorentz du jet 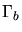 . On suppose que le facteur de
Lorentz du nodule est double de celui du jet et un temps caractéristique de variabilité de une heure.
. On suppose que le facteur de
Lorentz du nodule est double de celui du jet et un temps caractéristique de variabilité de une heure.
- CIB selon Macminn & Primack (1995) à z=0, pour des
hypothèses
de matière noire froide (CDM,
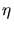 =0.9,
=0.9,
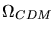 =0.1) et chaude+froide (CHDM,
=0.1) et chaude+froide (CHDM, 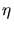 =0.6,
=0.6, 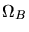 =0.3,
=0.3,
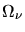 =0.1). Le modèle 1 correspond au spectre stellaire standard et
le modèle 2 à une supposition plus rouge.
=0.1). Le modèle 1 correspond au spectre stellaire standard et
le modèle 2 à une supposition plus rouge.
- Niveaux de
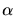 en fonction de l'indice spectral différentiel de
la source et du facteur d'échelle
en fonction de l'indice spectral différentiel de
la source et du facteur d'échelle
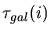 appliqué au CIB. Les lignes sont tracées
dans la zone autorisée, entre 95% et 98% de niveau de confiance.
appliqué au CIB. Les lignes sont tracées
dans la zone autorisée, entre 95% et 98% de niveau de confiance.
- Limites supérieures obtenues avec les données de CAT pour un indice
spectral de la source
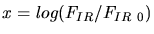 (pointillés), pour
(pointillés), pour 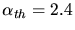 (tirets) et sans aucune hypothèse sur
(tirets) et sans aucune hypothèse sur 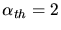 (trait plein). Les cercles sont les
limites
directes de COBE-DIRBE [204] et les carrés sont issus d'une nouvelle analyse menée
à partir des mesures de ce même instrument [199].
(trait plein). Les cercles sont les
limites
directes de COBE-DIRBE [204] et les carrés sont issus d'une nouvelle analyse menée
à partir des mesures de ce même instrument [199].
- Section efficace d'interaction
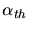 (unités arbitraires)
en fonction de
(unités arbitraires)
en fonction de 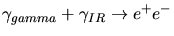 (keV) pour
(keV) pour 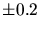 =1
TeV (courbe de droite) et mutliplication de cette section efficace par la
densité
de photons infrarouges (courbe de gauche).
=1
TeV (courbe de droite) et mutliplication de cette section efficace par la
densité
de photons infrarouges (courbe de gauche).
Aurelien Barrau
2004-07-01
 .
.
 .
.