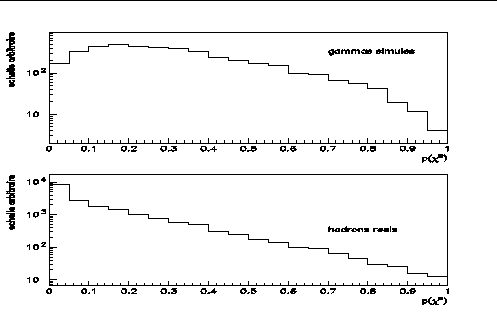
Comme le montre la figure 7.2, la variation du ![]() est
relativement lente dans une certaine plage. Il peut, de plus, exister dans
certains cas des minima
secondaires qui gênent la procédure de minimisation dans les appels
au programme
MINUIT (CERN) [68]. Le point faible de cette méthode réside dans
sa grande sensibilité aux conditions initiales: le point d'arrivée de
l'ajustement dépend fortement des valeurs proposées au départ de la mise en
oeuvre de l'algorithme. Les deux grandeurs dont l'estimation avant ajustement
est fondamentale sont le paramètre d'impact et l'énergie.
est
relativement lente dans une certaine plage. Il peut, de plus, exister dans
certains cas des minima
secondaires qui gênent la procédure de minimisation dans les appels
au programme
MINUIT (CERN) [68]. Le point faible de cette méthode réside dans
sa grande sensibilité aux conditions initiales: le point d'arrivée de
l'ajustement dépend fortement des valeurs proposées au départ de la mise en
oeuvre de l'algorithme. Les deux grandeurs dont l'estimation avant ajustement
est fondamentale sont le paramètre d'impact et l'énergie.
Pour le premier, un calcul semi-empirique utilisant la forme de la cascade mais
surtout le bon accord entre les simulations et la reconstruction a été
utilisé. La formule que nous avons obtenue de façon semi-empirique s'écrit:
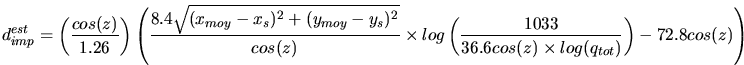 et
et
Il est important de noter que pour cette
évaluation la source est supposée de position connue dans le champ de la caméra.
En revanche, dans la procédure de minimisation de ![]() , les tests montrant qu'une
contrainte supplémentaire n'améliore pas la résolution (à condition
précisément que les conditions initiales soient correctes), cette position est
laissée libre. La méthode employée ici n'est donc pas encore réellement
adaptée à l'étude d'objets non localisés ou étendus.
, les tests montrant qu'une
contrainte supplémentaire n'améliore pas la résolution (à condition
précisément que les conditions initiales soient correctes), cette position est
laissée libre. La méthode employée ici n'est donc pas encore réellement
adaptée à l'étude d'objets non localisés ou étendus.
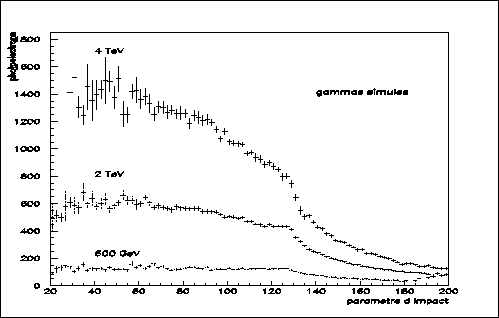
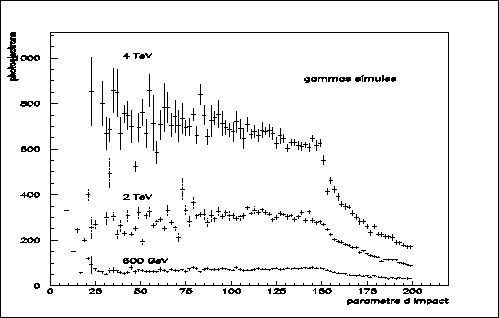
Pour estimer l'énergie du gamma, les figures 7.6 et 7.7
montrent (respectivement au zénith et à 30![]() ) que, pour un
paramètre d'impact donné, il est possible d'utiliser l'information contenue
dans la charge de l'image. La valeur de
) que, pour un
paramètre d'impact donné, il est possible d'utiliser l'information contenue
dans la charge de l'image. La valeur de 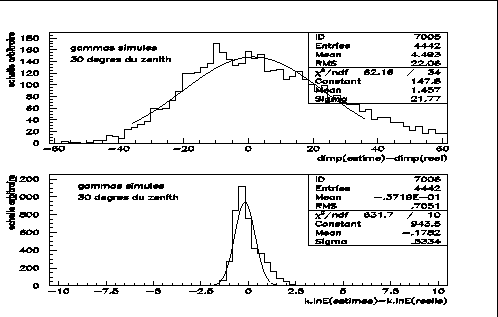 précédemment
mentionnée est alors prise en compte et l'énergie est calculée comme:
précédemment
mentionnée est alors prise en compte et l'énergie est calculée comme:
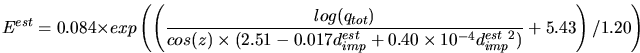 . Cette évaluation ne dépend, pour un
paramètre d'impact donné, que de la charge totale de l'image.
. Cette évaluation ne dépend, pour un
paramètre d'impact donné, que de la charge totale de l'image.
 |
Les 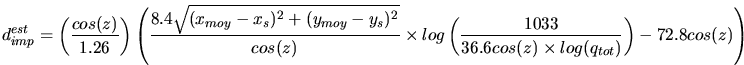 ,
, ![]() et
et ![]() utilisés pour
ces estimations ne sont pas exactement ceux qui seraient déduits de la simple
application des seuillages précédemment cités pour le calcul des moments de
Hillas. Des petits groupes de pixels touchés, hors du coeur de l'image, peuvent
effectivement être intéressants à prendre en compte dans le calcul des
paramètres de l'image: ils forment souvent une signature de gerbes hadroniques et
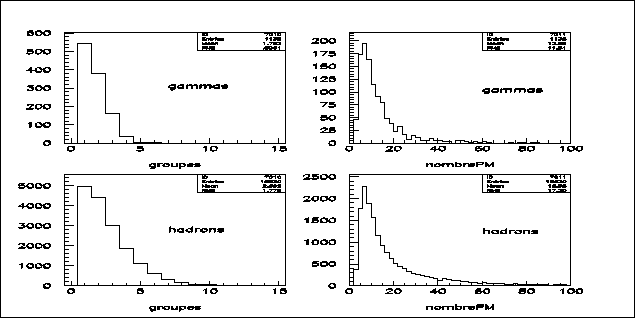
jouent donc un rôle important dans la réjection (cf figure 7.8).
En revanche, dans la
reconstruction des grandeurs physiques d'une cascade électromagnétique, ils
dégradent fortement la procédure, notamment dans l'évaluation des conditions
initiales. Pour cette raison, une routine de recherche de groupes de pixels est mise
en oeuvre. Celle-ci détermine le plus grand groupe de voies adjacentes touchées
(i.e. avec une charge supérieure à 2 photoélectrons)
dans la caméra. Seuls les signaux provenant de ces photomultiplicateurs sont
alors pris en
compte dans le calcul de la position du barycentre (essentielle à l'estimation
du paramètre d'impact) et de la charge totale (essentielle à l'estimation
de l'énergie).
utilisés pour
ces estimations ne sont pas exactement ceux qui seraient déduits de la simple
application des seuillages précédemment cités pour le calcul des moments de
Hillas. Des petits groupes de pixels touchés, hors du coeur de l'image, peuvent
effectivement être intéressants à prendre en compte dans le calcul des
paramètres de l'image: ils forment souvent une signature de gerbes hadroniques et
jouent donc un rôle important dans la réjection (cf figure 7.8).
En revanche, dans la
reconstruction des grandeurs physiques d'une cascade électromagnétique, ils
dégradent fortement la procédure, notamment dans l'évaluation des conditions
initiales. Pour cette raison, une routine de recherche de groupes de pixels est mise
en oeuvre. Celle-ci détermine le plus grand groupe de voies adjacentes touchées
(i.e. avec une charge supérieure à 2 photoélectrons)
dans la caméra. Seuls les signaux provenant de ces photomultiplicateurs sont
alors pris en
compte dans le calcul de la position du barycentre (essentielle à l'estimation
du paramètre d'impact) et de la charge totale (essentielle à l'estimation
de l'énergie).
 |
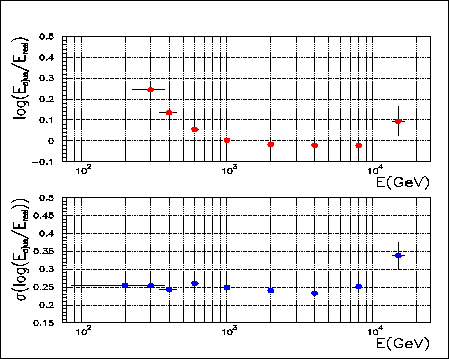
Les figures 7.9 et 7.10 donnent les performances de la méthode avec des gammas simulés après avoir utilisé ces nouveaux calculs de conditions initiales. La première est relative à la résolution en énergie obtenue. Pour quantifier celle-ci, on utilise le logarithme de la différence normalisée des énergies dont la distribution est gaussienne (ce qui est intéressant car la convolution avec une loi de puissance demeure gaussienne). La partie supérieure montre qu'entre 400 GeV et 15 TeV le biais est inférieur à 10%. L'apparition d'un effet systématique à faible énergie est une conséquence de la sélection par le système de déclenchement: les cascades soumises à des fluctuations positives du nombre de photoélectrons produits (dont l'énergie reconstruite est donc supérieure à l'énergie réelle) sont favorisées du point de vue de la probabilité de satisfaire à la condition de coïncidence majoritaire. La partie inférieure présente l'écart type de la gaussienne ajustée, c'est-à-dire un estimateur de résolution instrumentale sur la mesure de l'énergie. Elle est tout à fait constante à 25% jusqu'à 10 TeV. L'élargissement qui survient par la suite est un effet du modèle analytique non encore calculé pour les très hautes énergies.
 |
La seconde figure donne, dans la partie haute, la valeur moyenne de la gaussienne
ajustée sur la différence entre le paramètre d'impact reconstruit et le
paramètre d'impact simulé. Le biais est pratiquement nul (![]() 2.5 mètres)
dès 300 GeV. La partie inférieure montre que la résolution est meilleure
que 20 mètres dans cette même bande d'énergie et descend à 10 mètres
au-delà du TeV.
2.5 mètres)
dès 300 GeV. La partie inférieure montre que la résolution est meilleure
que 20 mètres dans cette même bande d'énergie et descend à 10 mètres
au-delà du TeV.
 |
En ce qui concerne la reconstruction angulaire de l'origine des gammas
simulés, la largeur de la distibution dépend du choix des coupures. Pour
l'analyse ici menée le 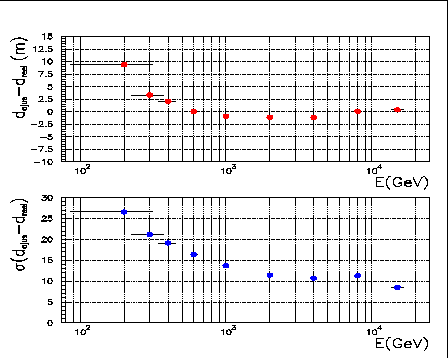 typique est de 0.14
typique est de 0.14![]() . Pour un événement
donné, la
précision atteinte perpendiculairement à la direction de l'axe principal est
2 fois supérieure à celle obtenue parallèlement à cet axe. Pour cette
raison, la variable d'angle de pointé
. Pour un événement
donné, la
précision atteinte perpendiculairement à la direction de l'axe principal est
2 fois supérieure à celle obtenue parallèlement à cet axe. Pour cette
raison, la variable d'angle de pointé ![]() est plus efficace que la
distance entre la position réelle de la source et la position reconstruite.
est plus efficace que la
distance entre la position réelle de la source et la position reconstruite.