Détermination exacte du piedestal

Le piedestal vrai, c'est-à-dire celui qui correspond au zéro électronique moyen, peut ainsi être déduit du piedestal apparent par une translation dépendant du bruit de fond de ciel. La correction à effectuer s'évalue en écrivant que la tension moyenne induite par les résidus d'impulsions sommés vaut (en considérant toutes les fonctions $V(x)$ avec le décalage approprié):

$$V_{moy}=\langle\sum_{n=0}^{\infty}V_{\gamma e}(x+n)\frac{1}{f}\rangle_{0<x<1}$$

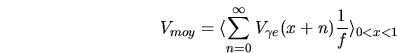où $V_{\gamma e}$ est la fonction de tension d'un photoélectron et 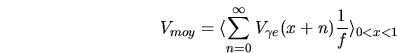$f$ la fréquence de bruit. En modélisant simplement $V_{\gamma e}$ par une exponentielle de constante caractéristique $\tau$, on obtient alors (avec $R$=50$~\Omega$):

$$V_{moy}=\frac{Q_{\gamma e}}{\tau}\frac{R}{1-e^{-\frac{1}{f\tau}}}\int_0^1e^{-\frac{x}{f\tau}}dx=Q_{\gamma e}fR$$

Cette évaluation est valable en régime de bruit faible. Lorsque le décalage atteint 1 photoélectron, on peut montrer [51] qu'il y a changement de régime et que l'écart recommence à diminuer (sous l'effet des impulsions qui tombent directement dans la porte). Dans la pratique, le décalage mesuré est de quelques canaux d'ADC, c'est-à-dire d'une fraction de photoélectron.

Figure 5.5: Histogramme des largeurs de piedestaux, en canaux ADC, sur les 546 voies internes moyennées sur un an.

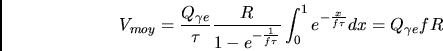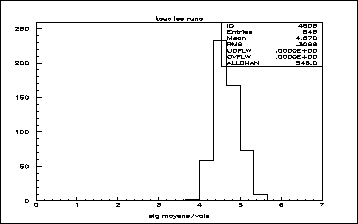
Pour chaque acquisition, un piedestal est ainsi calculé par voie. Sa largeur est utilisée par le programme d'analyse pour ignorer les canaux qui auraient subi un bruit électronique trop important. Généralement, elle demeure inférieure à un demi-photoélectron. La figure 5.5 présente la largeur du piedestal ($\approx$0.4 photoélectron) pour les 546 photomultiplicateurs internes, moyennée depuis le début du fonctionnement du télescope.

Pour la plupart des voies, le piedestal présente une remarquable stabilité de position en fonction du temps. La partie gauche de la figure 5.6 présente cette évolution pour un canal typique depuis le début du fonctionnement du télescope. La partie droite de cette figure présente l'évolution de la largeur (écart-type de la gaussienne ajustée) du piedestal de cette même voie. Il apparaît clairement que dans les conditions normales de fonctionnement l'électronique est très stable.

Figure 5.6: Gauche: évolution de la position du piedestal, en canaux ADC, de la voie 34 (typique) depuis le début du fonctionnement du télescope. Droite: même distribution pour la largeur du piedestal.