 |
La simple caractérisation des images à l'aide des paramètres de Hillas fondamentaux ne tient pas compte d'un paramètre essentiel: l'asymétrie du profil et sa dépendance avec la distance du "pied de gerbe" (c'est-à-dire le point d'arrivée extrapolé du gamma initial sur le terrain). La méthode employée consiste à comparer l'image obtenue à une base de données d'images théoriques. Celles-ci sont calculées à paramètre d'impact, énergie et angle zénithal données. Pour ce faire, il est possible d'évaluer les images attendues directement à partir des simulations [66] ou par l'intermédiaire d'un modèle analytique développé par S. Lebohec [40]. C'est cette seconde démarche qui est appliquée pour analyser les données de CAT. La structure de l'image Tcherenkov résulte à la fois du développement de la cascade de particules secondaires, de l'extension angulaire, des propriétés géométriques du rayonnement et des caractéristiques techniques du détecteur. Le but de cette approche est double:
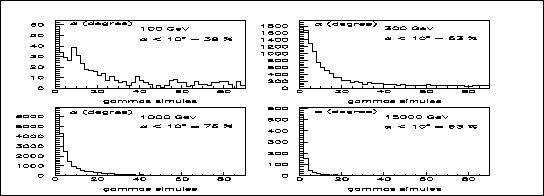
Le modèle analytique utilisé a été initialement développé par M. Hillas [65]. Un certain nombre des formules semi-empiriques utilisées ont néanmoins été modifiées de façon à assurer une correspondance fine entre l'image calculée et les simulations. La figure 7.1 montre le bon accord obtenu entre les distributions de lumière simulées et calculées pour différents paramètres d'impact. En particulier, les maxima secondaires attribués aux cas où les électrons suivant l'axe (c'est-à-dire les plus nombreux) "voient" le télescope exactement sous l'angle Tcherenkov, initialement présents dans le modèle [40], disparaissent après révision de la méthode d'intégration numérique. Le maximum principal est en revanche dû au nombre de particules dans le développement de la cascade et sa position demeure inchangée.
 |
Les modèles d'image ont été calculés à 11 angles zénithaux différents: 0,
18, 25, 30, 36, 41, 45, 49, 53, 56 et 60 degrés. Dans le traitement des données,
les modèles correspondant à l'angle zénithal dont le cosinus est le plus proche
de celui de l'événement sont utilisés.
Grâce à cette modélisation des images, il est donc possible de définir une charge théorique attendue dans chaque pixel de la caméra par intégration de la lumière sur l'angle solide couvert. Cette valeur dépend:
La qualité de l'ajustement du modèle par rapport à l'image réelle est
évaluée par une fonction de type ![]() définie par:
définie par:
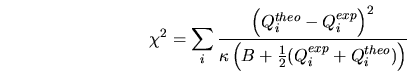 sont respectivement les charges
théoriques et expérimentales du
sont respectivement les charges
théoriques et expérimentales du
Par rapport aux études initiales, ce ![]() prend en compte le caractère
capacitif des liaisons entre les photomultiplicateurs et l'intégration
par les ADC. La présence de condensateurs assure effectivement une charge
transmise nulle en moyenne pour des signaux aléatoires. Il s'ensuit que le bruit
de fond de ciel ne doit pas apparaître explicitement au numérateur mais
doit en revanche être pris en compte comme terme de fluctuation
supplémentaire. La valeur numérique est calculée pour chaque acquisition
(de 30 minutes) en utilisant l'ensemble des pixels de la caméra
pour lesquels la qualité de l'ajustement de la fonction (présentée dans
la partie 2) est satisfaisante et n'ayant pas été soumis à
l'éclairement d'une étoile brillante. C'est donc le bruit de fond de ciel,
moyenné sur le temps et sur l'ensemble de la matrice de photomultiplicateurs,
qui est attribué à chaque terme du
prend en compte le caractère
capacitif des liaisons entre les photomultiplicateurs et l'intégration
par les ADC. La présence de condensateurs assure effectivement une charge
transmise nulle en moyenne pour des signaux aléatoires. Il s'ensuit que le bruit
de fond de ciel ne doit pas apparaître explicitement au numérateur mais
doit en revanche être pris en compte comme terme de fluctuation
supplémentaire. La valeur numérique est calculée pour chaque acquisition
(de 30 minutes) en utilisant l'ensemble des pixels de la caméra
pour lesquels la qualité de l'ajustement de la fonction (présentée dans
la partie 2) est satisfaisante et n'ayant pas été soumis à
l'éclairement d'une étoile brillante. C'est donc le bruit de fond de ciel,
moyenné sur le temps et sur l'ensemble de la matrice de photomultiplicateurs,
qui est attribué à chaque terme du ![]() .
.
La figure 7.2 présente les variations du ![]() pour deux
paramètres laissés arbitrairement libres (le paramètre d'impact et une quantité
proportionnelle au logarithme de l'énergie). La nappe obtenue montre
l'existence d'un minimum unique correspondant à la valeur de convergence. Ce
comportement se retrouve dans toutes les coupes.
pour deux
paramètres laissés arbitrairement libres (le paramètre d'impact et une quantité
proportionnelle au logarithme de l'énergie). La nappe obtenue montre
l'existence d'un minimum unique correspondant à la valeur de convergence. Ce
comportement se retrouve dans toutes les coupes.
De façon à s'affranchir du nombre variable de degrés de liberté d'un
évènement à l'autre, la probabilité de ![]() est utilisée comme
variable discriminante pour séparer les gammas des hadrons. Ce choix permet
de simplifier grandement l'analyse: les diverses coupures sur des
paramètres corrélés entre eux habituellement mises en oeuvre
(analyse sur les moments de Hillas) sont
remplacées par une unique coupure sur une variable incluant toute l'information.
En fonction de la nature de l'étude, la valeur peut être choisie
arbitrairement pour maximiser la signification statistique ou simplement le signal
résultant.
est utilisée comme
variable discriminante pour séparer les gammas des hadrons. Ce choix permet
de simplifier grandement l'analyse: les diverses coupures sur des
paramètres corrélés entre eux habituellement mises en oeuvre
(analyse sur les moments de Hillas) sont
remplacées par une unique coupure sur une variable incluant toute l'information.
En fonction de la nature de l'étude, la valeur peut être choisie
arbitrairement pour maximiser la signification statistique ou simplement le signal
résultant.
Pratiquement, la probabilité de ![]() n'est pas exactement calculée sur
la variable précédemment définie. Dans un premier temps, la valeur du
terme multiplicatif au dénominateur a été choisie à
n'est pas exactement calculée sur
la variable précédemment définie. Dans un premier temps, la valeur du
terme multiplicatif au dénominateur a été choisie à 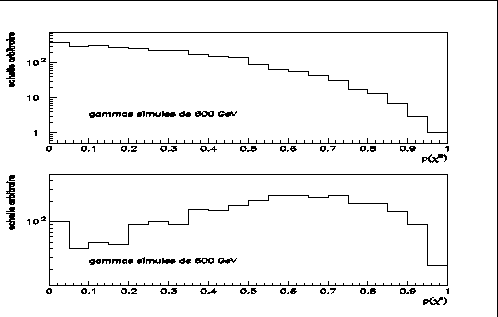 pour
tenir compte des fluctuations négligées et obtenir une distribution
relativement plate sur les gammas. Ensuite, une nouvelle grandeur est définie
par
pour
tenir compte des fluctuations négligées et obtenir une distribution
relativement plate sur les gammas. Ensuite, une nouvelle grandeur est définie
par
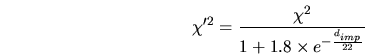 )
en fonction de
)
en fonction de
La figure 7.4 donne la comparaison des distribution de probabilité pour des gammas simulés en loi de puissance de la nébuleuse de Crabe entre 100 GeV et 10 TeV et des hadrons réels.
Dans la suite, pour ne pas alourdir la présentation, on utilisera toujours
![]() pour désigner la probabilité de
pour désigner la probabilité de ![]() .
.