 uvre" du modèle est néanmoins très
réduite.
uvre" du modèle est néanmoins très
réduite.
Dans ce modèle, les photons gamma observés en provenance de blazars sont
produits par des électrons soumis à une accélération linéaire
compensée par les pertes dues à l'effet Compton-inverse sur les photons
d'accrétion du disque. L'énergie maximum qui peut être atteinte pour un
objet tel que Mrk 501 avec des paramètres classiques de trou noir est de
l'ordre de 10 TeV, ce qui est compatible avec les énergies mises en évidence
par CAT. La "marge de man uvre" du modèle est néanmoins très
réduite.
uvre" du modèle est néanmoins très
réduite.
Deux caractéristiques du modèle doivent être notées. D'abord, il inclut
un mécanisme d'accélération explicite qui conduit naturellement à une
prédiction sur le site de production des gammas. Ensuite, le fait que les
collisions entre les électrons et les photons mous aient lieu dans le régime
de Thomson garantit que le gamma résultant sera en-dessous du seuil de
création de paires, évitant les complications d'une cascade
électromagnétique. Cette exigence est néanmoins posée de façon ad hoc.
Il reste de sérieuses contraintes à satisfaire pour que les photons puissent
quitter la source en évitant l'absorption sur le champ radiatif ambiant.
L'interaction avec la composante isotrope provenant de la diffusion des
radiations du disque [121] est supposée
négligeable dans ce modèle. Demeure la composante non-thermique qui est
directement observée. Celle-ci étant produite dans la zone
particulaire où les électrons ont eu le temps de former un nodule
relativiste radiatif, la profondeur optique est donnée, comme dans d'autres
modèles d'émission au GeV, par:
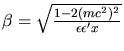 entre 0
et 1. L'intégrale sur
entre 0
et 1. L'intégrale sur 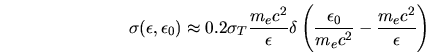 l'énergie de masse de
l'électron. Une telle simplification permet de faciliter grandement le calcul
des intégrales et ne modifie pas l'ordre de grandeur du résultat. La
profondeur optique s'écrit alors:
l'énergie de masse de
l'électron. Une telle simplification permet de faciliter grandement le calcul
des intégrales et ne modifie pas l'ordre de grandeur du résultat. La
profondeur optique s'écrit alors:
Par ailleurs, une contrainte additionnelle sur le facteur de Lorentz provient
des échelles de temps de la variabilité 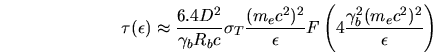 .
Considérant que le nodule se déplace directement vers l'observateur,
on obtient un facteur de Lorentz du nodule
.
Considérant que le nodule se déplace directement vers l'observateur,
on obtient un facteur de Lorentz du nodule
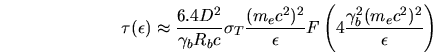 mesurés par CAT
conduisent donc à
mesurés par CAT
conduisent donc à