Pourquoi l'absorption est-elle "exponentielle"?
Dans cette annexe, l'énergie des gammas est notée ![]() et
l'énergie des photons infrarouges
et
l'énergie des photons infrarouges ![]() .
.
Pour une profondeur optique , le flux absorbé
s'écrit
![]() . Cependant cette équation ne
décrit pas l'absorption comme une
fonction exponentielle de l'énergie tant que la dépendance de
. Cependant cette équation ne
décrit pas l'absorption comme une
fonction exponentielle de l'énergie tant que la dépendance de ![]() en fonction
de
en fonction
de ![]() n'est pas explicitée.
Comme rappelé dans la dernière partie, la section efficace s'écrit
n'est pas explicitée.
Comme rappelé dans la dernière partie, la section efficace s'écrit
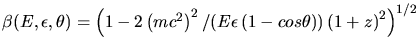 (dans le référentiel de
l'observateur).
L'interaction est bien-sûr soumise à un seuil
puisque l'énergie dans le centre de masse doit être suffisante pour créer des
paires. Il faut donc, pour
(dans le référentiel de
l'observateur).
L'interaction est bien-sûr soumise à un seuil
puisque l'énergie dans le centre de masse doit être suffisante pour créer des
paires. Il faut donc, pour
Comment
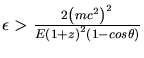 s'exprime-t-il en fonction de
s'exprime-t-il en fonction de
![]() ?
La
dépendance exacte est donnée (pour une densité de photons infrarouges de
?
La
dépendance exacte est donnée (pour une densité de photons infrarouges de
![]() cm
cm![]() ) par:
) par:
Il est possible de relier ![]() à
à ![]() pour étudier comment
varie la profondeur optique quand l'énergie est multipliée par
pour étudier comment
varie la profondeur optique quand l'énergie est multipliée par  .
Dans l'expression de
.
Dans l'expression de ![]() , les énergies
, les énergies ![]() et
et ![]() n'interviennent que par leur produit. La section efficace s'écrit ainsi
n'interviennent que par leur produit. La section efficace s'écrit ainsi
![]() =
=
![]() . Pour simplifier le problème,
considérons un fond infrarouge constant (hypothèse tout à fait raisonnable) de
10 nW/m
. Pour simplifier le problème,
considérons un fond infrarouge constant (hypothèse tout à fait raisonnable) de
10 nW/m![]() /sr. Puisque c'est la
densité volumique d'énergie que l'on fixe, on a en fait
/sr. Puisque c'est la
densité volumique d'énergie que l'on fixe, on a en fait
![]() .
.
On peut donc écrire l'expression de ![]() en remplaçant
en remplaçant ![]() par sa valeur:
par sa valeur:
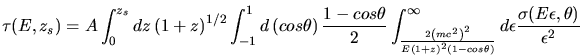 est la constante qui "incorpore" tout ce qui ne varie pas (
est la constante qui "incorpore" tout ce qui ne varie pas (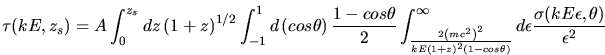 :
:
On a ainsi montré de façon très simple
(dans l'hypothèse physique d'un fond infrarouge tel que
![]() =cte) que
=cte) que
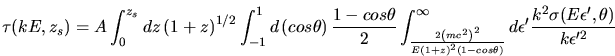 .
.
Ce résultat prouve que
si le flux s'écrit
![]() , il est soumis à une absorption
exponentielle en fonction de l'énergie, ce qui n'est pas vrai a
priori pour une distribution spectrale quelconque du CIB. Si l'on considère
des formes plus élaborées en
, il est soumis à une absorption
exponentielle en fonction de l'énergie, ce qui n'est pas vrai a
priori pour une distribution spectrale quelconque du CIB. Si l'on considère
des formes plus élaborées en
![]() , il est clair que la
dépendance de
, il est clair que la
dépendance de ![]() en
en ![]() ne sera plus simplement linéaire
comme dans le cas précédemment étudié.
ne sera plus simplement linéaire
comme dans le cas précédemment étudié.
Le point fondamental est de bien noter que la forme mathématique de la section
efficace et le fait que le CIB est à peu près constant (en
![]() c'est-à-dire qu'il décroît très vite en
c'est-à-dire qu'il décroît très vite en ![]() impliquent une
absorption exponentiellement décroissante (i.e.
impliquent une
absorption exponentiellement décroissante (i.e. ![]() linéairement
croissant). Il est intéressant de remarquer que, inversement,
linéairement
croissant). Il est intéressant de remarquer que, inversement,
![]() serait une fonction linéairement décroissante de
l'énergie si on avait
serait une fonction linéairement décroissante de
l'énergie si on avait
![]() .
.
Dépendance en ![]() , sensibilité à la densité et à la longueur d'onde
, sensibilité à la densité et à la longueur d'onde
Tout d'abord, on peut vérifier que plus la source étudiée présente un grand
![]() , plus la "coupure" se produit à basse énergie. Effectivement, la coupure du
spectre par l'exponentielle d'absorption a lieu quand la profondeur
optique devient, pour fixer les idées, supérieure à 1.
Mais dans les formules précédentes, il y a
aussi une intégrale sur
, plus la "coupure" se produit à basse énergie. Effectivement, la coupure du
spectre par l'exponentielle d'absorption a lieu quand la profondeur
optique devient, pour fixer les idées, supérieure à 1.
Mais dans les formules précédentes, il y a
aussi une intégrale sur ![]() : quand on propage la somme sur une plus grande distance,
l'interaction intervient d'avantage et l'énergie à laquelle
: quand on propage la somme sur une plus grande distance,
l'interaction intervient d'avantage et l'énergie à laquelle ![]() devient supérieur à 1 est de plus en plus basse.
devient supérieur à 1 est de plus en plus basse.
Une expérience gamma peut être considérée comme sensible à une absorption
infrarouge si
la "cassure", c'est-à-dire l'énergie à laquelle la profondeur optique devient
plus
grande que 1, se trouve dans la gamme de sensibilité du détecteur. Pour CAT,
on peut calculer à l'aide des formules précédentes que le
détecteur est sensible
à un fond CIB compris entre environ 1.6 nW/m![]() /sr et 79 nW/m
/sr et 79 nW/m![]() /sr pour une
source très proche comme Mrk421 ou Mrk501.
/sr pour une
source très proche comme Mrk421 ou Mrk501.
En ce qui concerne la gamme d'énergies infrarouges qu'une expérience gamma est en mesure
de sonder,
on peut admettre que c'est celle pour laquelle la section efficace d'interaction
avec les gammas est importante (en tous cas pour des sources proches).
En fait, l'ensemble du spectre infrarouge intervient à toutes
les énergies de gammas puisque les intégrales se font jusqu'à l'infini. La
figure B.1 montre néanmoins que la section efficace est assez piquée.
La longueur
d'onde infrarouge à laquelle elle est maximale est
![]()
![]() m. On estime donc que les longueurs d'onde préférentiellement sondées
par CAT
se trouvent entre 0.7 et 24
m. On estime donc que les longueurs d'onde préférentiellement sondées
par CAT
se trouvent entre 0.7 et 24 ![]() m. Mais, en-dessous du TeV, la section efficace
décroît lentement avec l'énergie du photon IR (au-delà du maximum) et cet
intervalle est
en fait arbitraire. A 600 GeV, par exemple, la section efficace n'a diminué
que de 30 % pour une énergie infrarouge 3 fois supérieure à l'énergie qui
maximise l'interaction. Ce qui signifie que s'il existe bien-sûr une borne
inférieure (gamma de 15 TeV en collision frontale
m. Mais, en-dessous du TeV, la section efficace
décroît lentement avec l'énergie du photon IR (au-delà du maximum) et cet
intervalle est
en fait arbitraire. A 600 GeV, par exemple, la section efficace n'a diminué
que de 30 % pour une énergie infrarouge 3 fois supérieure à l'énergie qui
maximise l'interaction. Ce qui signifie que s'il existe bien-sûr une borne
inférieure (gamma de 15 TeV en collision frontale ![]()
![]() eV), les photons infrarouges interviennent de façon non
négligeable jusqu'à des énergies très importantes, c'est l'effet
conjugué de l'angle qui peut être faible et de la section efficace qui
décroit assez lentement. La notion de fenêtre de sensibilité IR
n'est pas clairement définie et il est de plus nécessaire de
supposer une forme de l'ensemble du spectre qui ne peut être que modifiée
par un facteur d'échelle pour une observation gamma.
eV), les photons infrarouges interviennent de façon non
négligeable jusqu'à des énergies très importantes, c'est l'effet
conjugué de l'angle qui peut être faible et de la section efficace qui
décroit assez lentement. La notion de fenêtre de sensibilité IR
n'est pas clairement définie et il est de plus nécessaire de
supposer une forme de l'ensemble du spectre qui ne peut être que modifiée
par un facteur d'échelle pour une observation gamma.