La méthode utilisée pour contraindre la densité du CIB consiste à comparer le
spectre expérimental de Mrk501 (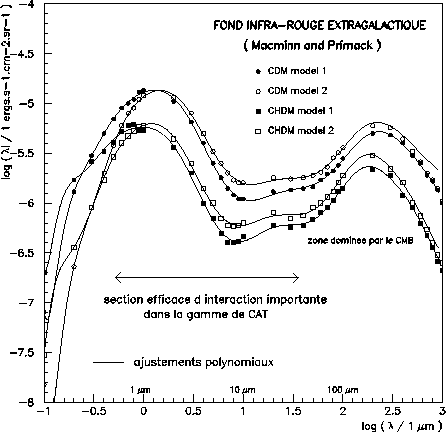 ) à un spectre calculé prenant en compte les effets
d'absorption par l'infrarouge [218].
) à un spectre calculé prenant en compte les effets
d'absorption par l'infrarouge [218].
Etant donné que la forme exacte du flux différentiel intrinsèque de la source n'est
pas connue, différentes hypothèses d'indice spectral différentiel ![]() (exposant de la loi de puissance d'émission) sont faites
pour des valeurs variant continuement entre 1 et 3.
La seule supposition sur Mrk501 consiste donc à considérer que la distribution
énergétique des photons émis suit une loi de puissance, ce qui est suggéré par
toutes les données observationnelles disponibles sur les AGN.
(exposant de la loi de puissance d'émission) sont faites
pour des valeurs variant continuement entre 1 et 3.
La seule supposition sur Mrk501 consiste donc à considérer que la distribution
énergétique des photons émis suit une loi de puissance, ce qui est suggéré par
toutes les données observationnelles disponibles sur les AGN.
Le spectre théorique absorbé a été ici calculé en utilisant les formules de
section efficace et de profondeur optique données au paragraphe Interaction des photons gamma VHE avec le CIB avec des facteurs d'échelles compris
entre ![]() et
et ![]() pour 2 formes différentes: celle du modèle de Macminn et
Primack, et une supposée constante en
pour 2 formes différentes: celle du modèle de Macminn et
Primack, et une supposée constante en
![]() avec un flux
d'énergie
avec un flux
d'énergie
![]() nW.m
nW.m![]() .sr
.sr![]() =
10
=
10![]() ergs
ergs![]() .cm
.cm![]() .sr
.sr![]() , ce qui est une valeur canonique sur la gamme
de longueurs d'ondes couvertes par CAT [199].
, ce qui est une valeur canonique sur la gamme
de longueurs d'ondes couvertes par CAT [199].
Le flux résultant a été normalisé aux données expérimentales dans le premier
des ![]() intervalles d'énergie entre 250 GeV et 15 TeV. La qualité de l'ajustement est évaluée par:
intervalles d'énergie entre 250 GeV et 15 TeV. La qualité de l'ajustement est évaluée par:
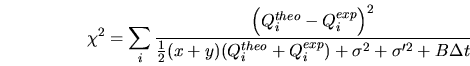 est le logarithme décimal du facteur d'échelle,
est le logarithme décimal du facteur d'échelle, 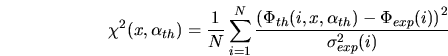 est l'erreur statistique
expérimentale et
est l'erreur statistique
expérimentale et
Les calculs numériques sont menés avec un paramètre de Hubble ![]() de 65
km.s
de 65
km.s![]() Mpc
Mpc![]() , qui se situe dans la moyenne des mesures les plus récentes
[219] [220].
, qui se situe dans la moyenne des mesures les plus récentes
[219] [220].
Le ![]() résultant est tracé sur la figure 13.2 en fonction de
l'indice spectral
résultant est tracé sur la figure 13.2 en fonction de
l'indice spectral ![]() de la source et de
de la source et de
![]() , avec
, avec ![]() le
flux infra-rouge testé, pour le
profil de Macminn & Primack (partie supérieure,
le
flux infra-rouge testé, pour le
profil de Macminn & Primack (partie supérieure, ![]() est alors arbitrairement
choisie comme le modèle CDM 1) et pour l'hypothèse constante
(partie inférieure, avec
est alors arbitrairement
choisie comme le modèle CDM 1) et pour l'hypothèse constante
(partie inférieure, avec
![]() nW.m
nW.m![]() .sr
.sr![]() ). Les lignes présentent des niveaux de
). Les lignes présentent des niveaux de ![]() équidistants et
la large surface blanche correspond à la zone exclue à 95% de confiance.
équidistants et
la large surface blanche correspond à la zone exclue à 95% de confiance.