Cônes de Winston

Figure 4.14: Concentration de la lumière par un cône de Winston (partie supérieure) sur un photomultiplicateur (partie inférieure). Figure LPNHE-X.

La photocathode des photomultiplicateurs étant de diamètre inférieur au tube lui-même, l'espace "sensible" pavé par le réseau hexagonal compact n'est que d'environ 35% de la surface totale. Celui-ci peut être considérablement augmenté en utilisant des petits "entonnoirs de lumière": les cônes de Winston [44] (cf figure 4.14). Leur premier rôle consiste donc à utiliser au mieux la surface de la caméra. Dans l'idéal, un réseau de disques jointifs couvre 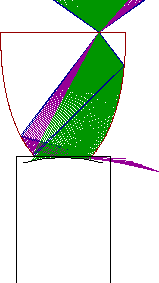$\frac{\pi}{4cos\frac{\pi}{6}}=91 \%$ de l'aire. Compte-tenu de l'épaisseur de matière des cônes, la proportion de la surface pavée est dans le cas présent de 88%. Le dimaètre intérieur de la face d'entrée des cônes est de 12.8 mm sur les pixels internes et de 42.0 mm pour les pixels de garde.

Le second rôle des cônes consiste à écarter la lumière d'albedo. L'angle sous lequel le miroir est vu depuis la caméra étant d'environ 30 degrés, tout photon venant avec une incidence plus grande est nécessairement une lumière parasite. La géométrie des cônes permet de rejeter efficacement les photons tout en atténuant très peu ceux provenant du miroir, comme le montre la figure 4.15.

Figure 4.15: Efficacité des cônes en fonction de l'angle d'incidence de la lumière.

Ces éléments ne sont néanmoins pas parfaits et leur efficacité de réflexion doit être mesurée en fonction de la longueur d'onde. Reste donc à évaluer la probabilité qu'un photon arrivant sur la surface d'entrée du cône parvienne jusqu'à la photocathode du photomuliplicateur. Cette valeur, qu'on appelle réflectivité du cône, tient implicitement compte du fait que certains photons parviennent directement sur le photomultiplicateur tandis que d'autres sont réfléchis par le cône. L'écart par rapport à l'unité provient des photons arrivant des bords du miroir (c'est-à-dire avec des angles proches de 30 degrés) et de la réflectivité intrinsèque du cône.

Le but de la mesure est d'évaluer la réflectivité des cônes à différentes longueurs d'onde pour des photons arrivant exactement avec la distribution d'angles qu'ils auraient en provenant du miroir.

Pour ce faire, une lampe à arc de spectre large a été utilisée. Le faisceau de sortie traverse d'abord un filtre interférentiel de faible largeur spectrale. Il est ensuite atténué puis diffusé. La lumière résultante, homogène, atteint d'une part un photomultiplicateur de référence qui permet de s'affranchir des éventuelles variations de la lampe, d'autre part un second diffuseur hexagonal qui reproduit la forme du miroir. Ce diffuseur est vu par le photomultiplicateur de test sous le même angle solide que le miroir du télescope depuis la caméra. L'ensemble est placé dans une enceinte dont l'étanchéité à la lumière a été vérifiée. Le photomultiplicateur de test est alternativement utilisé avec et sans cône. Dans ce dernier cas, la partie extérieure de la photocathode est masquée de façon que les photons tombent exactement dans la même région qu'en sortant du cône, évitant ainsi tout artéfact dû à l'inhomogénéite de l'efficacité de collection du photomultiplicateur. Toutes les mesures sont faites par comparaison des résultats avec et sans cône dans des conditions identiques (après correction des fluctuations de la lampe à l'aide du photomultiplicateur de référence). La figure 4.16 donne la synoptique du montage.

Figure 4.16: Montage utilisé pour la caractérisation des cônes.

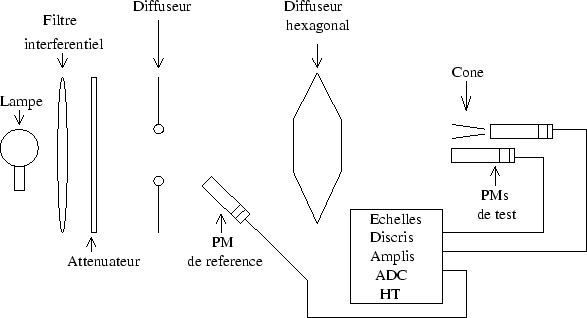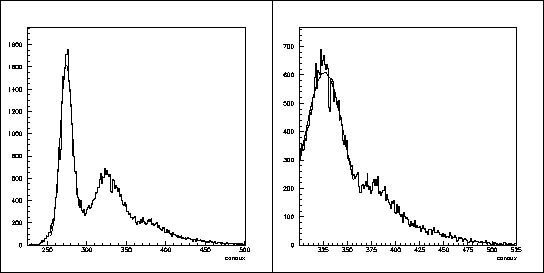
Les enregistrements ont été effectués avec un convertisseur analogique-numérique Lecroy 10 bits 2249 déclenché en porte aléatoire large (200 ns). Cette façon de procéder permet d'éviter différents problèmes liés aux échelles de comptage lorsque la lumière est de faible intensité. La haute tension a été portée à sa valeur maximale (1500V), le gain du photomultiplicateur avoisinant alors $4\times10^6$.

La principale difficulté provient du changement de régime qui a lieu lorsque le signal du photomultiplicateur varie en intensité (effet de la convolution des différentes efficacités, du spectre d'émission et de la largeur des filtres):

• En régime de forte lumière, la porte d'intégration contient toujours plusieurs photoélectrons et le spectre ADC se présente sous la forme d'une gaussienne dont la valeur moyenne (déduction faite du piedestal) est directement proportionnelle à la quantité de lumière reçue. En accumulant une statistique importante, les résultats sont parfaitement reproductibles.

• En régime de faible lumière, la porte d'intégration ne contient plus systématiquement des photoélectrons. Le piedestal, le spectre de photoélectron unique et la "traînée" des évènements à plusieurs photoélectrons sont ainsi visibles. La valeur moyenne n'est plus une mesure de la quantité de lumière reçue. On utilise alors le rapport de la quantité de coups dans le piedestal (n) sur le nombre total d'acquisitions (N) qui mesure la probabilité de n'avoir aucun photoélectron, c'est-à-dire $e^{-f\Delta t}$ pour une loi de Poisson (où $f$ est la fréquence de la lumière et $\Delta t$ la largeur de la porte). Le gain du photomultiplicateur utilisé étant important (de l'ordre de $4\times10^6$), le piedestal est suffisamment éloigné du pic à un photoélectron (plus de 50 canaux) pour que le choix des coupures soit sans réelles conséquences. Le rapport des fréquences entre les mesures avec et sans cône s'exprime donc par:
  
  $$\frac{f_{avec}}{f_{sans}}=\frac{ln(\frac{N_{avec}}{n_{avec}})}{ln(\frac{N_{sans}}{n_{sans}})}$$
  
  

Toutes les mesures sont ensuite renormalisées au rapport des surfaces.

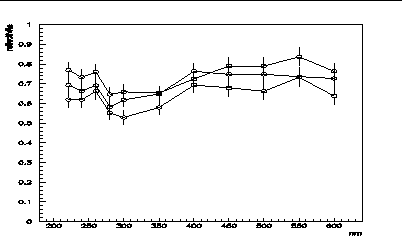
La Figure 4.17 présente les résultats avec les cônes testés.

Figure 4.17: Réflectivité effective des trois cônes testés.

L'allure identique des courbes montre la reproductibilité des résultats et la dispersion qui apparaît (de l'ordre de 10%) est tout-à-fait compatible avec les mesures précédemment effectuées sur les corrections optiques (somme quadratique des dispersions des cônes et des efficacités quantiques)

La valeur moyenne des cônes testés est prise en compte dans les simulations et dans les progammes de génération de modèle analytique décrit dans la troisième partie de ce mémoire. Sur l'échantillon dont on dispose, cette démarche est justifiée par le fait que l'écart-type est du même ordre de grandeur que l'erreur de mesure.

On peut noter que cette valeur est bien compatible avec les courbes présentées à la figure 4.15 pour évaluer l'effet du cône en fonction de l'angle d'incidence. Cette mesure a été effectuée à 450 nm. La réflectivité moyenne pour les photons venant du miroir peut en effet se calculer:

$$\frac{1}{\pi \theta_{max}^2} \int_0^{\theta_{max}} 2\pi \theta R \left(\theta\right) d\theta$$

où $R\left(\theta\right)$ est la réflectivité à l'angle $\theta$ et $\theta_{max}=Arctan\left(\frac{focale}{rayon}\right)$. En tenant compte du rapport des surfaces du cône et du photomultiplicateur seul ainsi que du gain en efficacité de collection avec le cône (qui concentre les photons au centre de la photocathode), on obtient une réflectivité de 72%, ce qui est parfaitement compatible avec les mesures présentées en 4.17.

L'effet des cônes sur le spectre Tcherenkov, à différentes altitudes d'émission est donné sur la Figure 4.18.

Figure 4.18: Effet des cônes sur la lumière Tcherenkov. La courbe en pointillés donne le spectre d'émission de la lumière Tcherenkov (divisé par 4 pour la lisibilité), la courbe en tirets est le résultat de la multiplication par l'efficacité quantique de la photocathode et la courbe en trait plein est identique à la précédente après ajout de l'effet des cônes. L'ensemble est représenté à différentes altitutes d'émission (de 0 à 16 km) et il apparaît que la fraction de lumière perdue par les cônes demeure constante.