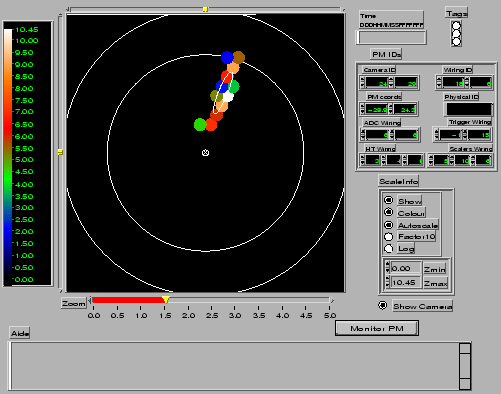
Le groupe d'astronomie gamma de l'observatoire de Whipple a été le
premier à mettre en oeuvre la technique d'imagerie. La méthode
employée consiste à modéliser la distribution de lumière dans le plan
focal par une gaussienne bidimentionnelle caractérisée par ses directions
principales et les écarts-types associés. Cette démarche, initiée par
M. Hillas [65] et ultérieurement améliorée, est ici rappelée
car elle permet de déterminer les conditions initiales du maximum de
vraisemblance utilisé par CAT.
Dans l'analyse de type "Hillas", différentes grandeurs sont évaluées pour chaque image obtenue (figure 6.4):

Avec ![]() la charge en photoélectrons du
la charge en photoélectrons du ![]() pixel de
coordonnées
pixel de
coordonnées 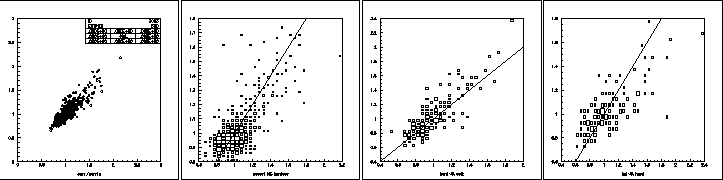 et
et ![]() , on note
, on note
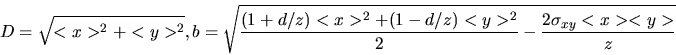
Les paramètres ainsi définis sont représentés sur la figure 6.4
Pour déterminer les valeurs des contenus de chaque pixel, les images sont
d'abord nettoyées pour éviter qu'un dysfonctionnement technique ou qu'un
signal venant du bruit de fond de ciel ne modifie arbitrairement les
caractéristiques. La charge ![]() d'un pixel (en photoélectrons) est mise
à zéro si:
d'un pixel (en photoélectrons) est mise
à zéro si:
Avec cette caractérisation des images, la sélection des cascades
électromagnétiques parmi l'ensemble des événements déclenchant le
télescope peut s'effectuer à la fois sur des critères de forme
(![]() et
et ![]() ) et des critères d'orientation (
) et des critères d'orientation (![]() ,
,![]() et
et  ). Dans
notre cas, seules des coupures préliminaires très "larges" sur la forme
(
). Dans
notre cas, seules des coupures préliminaires très "larges" sur la forme
(![]() mrad et
mrad et ![]() mrad)
sont appliquées avant de mettre en oeuvre le maximum de vraisemblance.
Environ 25% des événements sont ainsi rejetés (évalué sur les données
réelles) et seulement 2% des gammas sont perdus (évalué sur des gammas
simulés en loi de puissance du Crabe).
mrad)
sont appliquées avant de mettre en oeuvre le maximum de vraisemblance.
Environ 25% des événements sont ainsi rejetés (évalué sur les données
réelles) et seulement 2% des gammas sont perdus (évalué sur des gammas
simulés en loi de puissance du Crabe).
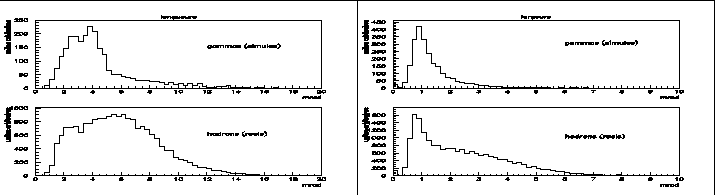
La partie gauche de la figure 6.5 présente la distribution des
![]() pour des
photons gamma simulés en loi de puissance et pour un fond de rayons
hadroniques obtenu à partir des données réelles en visant hors du champ de
toute source gamma potentielle. La moitié droite présente de façon
analogue l'histogramme des
pour des
photons gamma simulés en loi de puissance et pour un fond de rayons
hadroniques obtenu à partir des données réelles en visant hors du champ de
toute source gamma potentielle. La moitié droite présente de façon
analogue l'histogramme des ![]() . L'étude systématique des critères de
coupures sur ces paramètres n'a pas été menée dans le cas de
CAT car la méthode d'analyse utilisée exploite davantage l'information
contenue dans les pixels de l'image. Il apparaît néanmoins qu'une part
importante (
. L'étude systématique des critères de
coupures sur ces paramètres n'a pas été menée dans le cas de
CAT car la méthode d'analyse utilisée exploite davantage l'information
contenue dans les pixels de l'image. Il apparaît néanmoins qu'une part
importante (![]() ) du fond peut-être rejetée en perdant peu de
gammas (
) du fond peut-être rejetée en perdant peu de
gammas (![]() ) sur de simples considérations de forme (0.7 mrad
) sur de simples considérations de forme (0.7 mrad
![]() 1.5 mrad et 2.0 mrad
1.5 mrad et 2.0 mrad ![]() 5.0 mrad).
5.0 mrad).
Les distributions des angles de pointé
![]() entre le grand axe de l'ellipse approximant l'image et la droite joignant le
centre du champ au barycentre sont représentées sur la figure 6.6.
Cette variable est distribuée entre 0 et 90 degrés
étant donné que dans le cadre de la paramétrisation de Hillas l'axe n'est pas orienté.
C'est une grandeur très discriminante puisque l'histogramme équivalent pour le
fond hadronique (et pour les muons) est plat (comme présenté dans la dernière
partie sur les différentes figures obtenues "OFF-source") consécutivement à
l'isotropie des directions d'arrivée des rayons cosmiques chargés. La précision
avec laquelle cet angle est estimé dépend fortement de l'énergie: le
nombre d'événements gamma pour lesquels
entre le grand axe de l'ellipse approximant l'image et la droite joignant le
centre du champ au barycentre sont représentées sur la figure 6.6.
Cette variable est distribuée entre 0 et 90 degrés
étant donné que dans le cadre de la paramétrisation de Hillas l'axe n'est pas orienté.
C'est une grandeur très discriminante puisque l'histogramme équivalent pour le
fond hadronique (et pour les muons) est plat (comme présenté dans la dernière
partie sur les différentes figures obtenues "OFF-source") consécutivement à
l'isotropie des directions d'arrivée des rayons cosmiques chargés. La précision
avec laquelle cet angle est estimé dépend fortement de l'énergie: le
nombre d'événements gamma pour lesquels
 évolue de 39% à
93% entre 100 GeV et 15 TeV.
évolue de 39% à
93% entre 100 GeV et 15 TeV.
L'optimisation des coupures sur les paramètres de Hillas est assez délicate dans la mesure où elle nécessite de tenir compte de 6 paramètres qui ne sont pas indépendants. Les bornes doivent, de plus, dépendre de l'énergie (qui est elle-même une grandeur à estimer) et de l'angle zénithal.
Dans la démarche choisie pour l'exploitation de l'imageur CAT, fondée sur une analyse par maximum de vraisemblance, à la fois simple dans son principe et précise dans ses résultats, les moments géométriques de Hillas ne sont utilisés que pour estimer les conditions initiales de l'ajustement.