La détermination de l'acceptance du détecteur, de l'efficacité des
coupures, du temps mort d'acquisition et des critères de sélection de
données est essentielle pour obtenir des flux quantitatifs et des variations
correctement étalonnées à partir des données enregistrées. C'est une
procédure indispensable de déconvolution des effets instrumentaux.
L'acceptance est l'intégrale de l'efficacité de détection 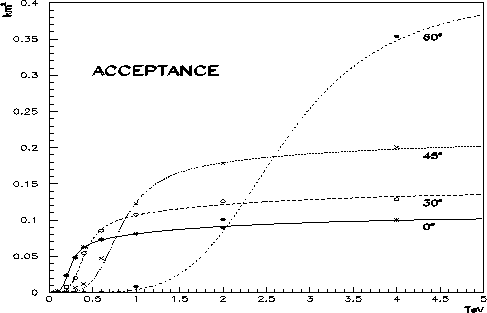 dans un plan perpendiculaire à la direction de visée du télescope:
dans un plan perpendiculaire à la direction de visée du télescope:
L'acceptance a été ainsi calculée pour des photons gamma de 0.05, 0.10,
0.20, 0.30, 0.40, 0.60, 1.0, 2.0, 4.0, 8.0 et 15.0 TeV à 0, 30, 45 et 60
degrés du zénith. Le nombre d'événements générés doit être plus
important à faible énergie (![]() 100000 gerbes) pour compenser la grande
perte de statistique dûe
au déclenchement et le paramètre d'impact maximum doit augmenter avec
l'énergie et l'angle zénithal (jusqu'à
100000 gerbes) pour compenser la grande
perte de statistique dûe
au déclenchement et le paramètre d'impact maximum doit augmenter avec
l'énergie et l'angle zénithal (jusqu'à
![]() mètres
pour des gammas de 15 TeV à
mètres
pour des gammas de 15 TeV à ![]() de site).
de site).
Les résultats obtenus permettent une paramétrisation analytique de la fonction d'acceptance:
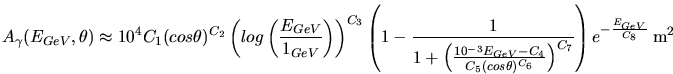 est l'énergie du gamma en GeV,
est l'énergie du gamma en GeV,
| Constantes | ||||||||
| Valeurs | 1.7239 | -1.9823 | 1.4263 |
|
0.2341 | -3.4702 | 4.6552 | 55055 |
La fonction ainsi déterminée permet de connaître une surface effective
pour chaque événement, une fonction de l'angle de pointé et de l'énergie
reconstruite. Le figure 8.1 présente la forme de
![]() . Il apparaît nettement qu'à faible
énergie, l'acceptance est plus importante près du zénith, par effet de
seuil, tandis qu'à haute énergie, elle devient plus grande à petit angle
de site, par effet géométrique d'augmentation de surface. On peut
également noter que le terme multiplicatif
. Il apparaît nettement qu'à faible
énergie, l'acceptance est plus importante près du zénith, par effet de
seuil, tandis qu'à haute énergie, elle devient plus grande à petit angle
de site, par effet géométrique d'augmentation de surface. On peut
également noter que le terme multiplicatif
![]() présent dans la formule analytique induit une légère
baisse d'acceptance au-delà d'une dizaine de TeV: c'est la conséquence des
images qui commencent à sortir de la zone de déclenchement de la caméra.
présent dans la formule analytique induit une légère
baisse d'acceptance au-delà d'une dizaine de TeV: c'est la conséquence des
images qui commencent à sortir de la zone de déclenchement de la caméra.
En multipliant l'acceptance par le flux d'une source, on obtient un taux de
déclenchement différentiel. Ce nombre d'événements par seconde et par TeV
est représenté à la figure 8.2 pour le flux supposé de la
nébuleuse du Crabe. Bien que la définition demeure très arbitraire, on
peut évaluer le seuil du détecteur par le maximum de chacune des courbes
ainsi représentées. Il varie entre 250 et 350 GeV pour un angle zénithal
d'observation inférieur à 30![]() .
.
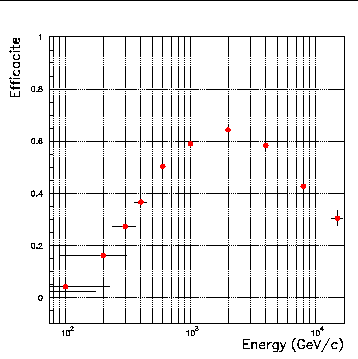
L'efficacité de reconstruction est une autre grandeur dont la connaissance est
essentielle pour estimer et corriger l'effet des coupures appliquées
dans l'analyse. La méthode développée pour exploiter les données de CAT
reposant principalement sur une unique variable (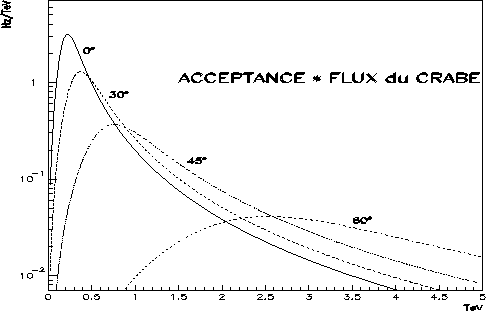 ), l'évaluation de
cette efficacité se trouve grandement simplifiée. C'est bien-sûr une
fonction de l'énergie, c'est-à-dire de l'une des valeurs physiques à
estimer. La figure 8.3 présente la fraction des événements
gammas simulés conservés par les coupures suivantes:
), l'évaluation de
cette efficacité se trouve grandement simplifiée. C'est bien-sûr une
fonction de l'énergie, c'est-à-dire de l'une des valeurs physiques à
estimer. La figure 8.3 présente la fraction des événements
gammas simulés conservés par les coupures suivantes:
Le temps mort d'acquisition doit être connu pour évaluer correctement le
flux de la source étudiée. La figure 8.4 montre la
distribution poissonnienne des intervalles de
temps entre deux événements successifs enregistrés. Le temps mort de
conversion apparaît au début de l'histogramme. Pour évaluer
précisément le nombre total d'événements qui auraient du être acquis à
partir du nombre effectivement obtenu, on procède d'abord à un ajustement de
fonction exponentielle (de constante ![]() ) sur la distribution. La
correction s'écrit:
) sur la distribution. La
correction s'écrit: