



Next: Détermination exacte du piedestal
Up: Piedestaux
Previous: Simulation
Contents
Le bruit de fond de ciel provient de la lumière des étoiles, des nébuleuses, de la
Voie Lactée, des éclairages urbains et de certaines sources parasites
imprévisibles.
Sa connaissance est importante à
deux niveaux au moins: d'une part comme indicateur de la qualité du ciel et d'autre part
pour déterminer le piedestal vrai à partir du piedestal apparent ajusté sur les
histogrammes ADC.
Afin de mesurer le fond de ciel, des événements logiciels aléatoires intégrant le
signal sur un temps plus long (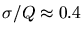 ns) sont générés tous les dix
événements réels. La valeur exacte du bruit est déterminée par ajustement d'une
fonction
ns) sont générés tous les dix
événements réels. La valeur exacte du bruit est déterminée par ajustement d'une
fonction 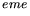 (dans le cas où la valeur reste inférieure à quelques photoélectrons
par porte, ce qui est le régime habituel) déterminée de façon "semi-empirique":
(dans le cas où la valeur reste inférieure à quelques photoélectrons
par porte, ce qui est le régime habituel) déterminée de façon "semi-empirique":
où 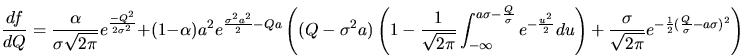 est la charge après déduction de l'effet de fond de ciel,
est la charge après déduction de l'effet de fond de ciel,
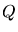 avec
avec 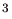 le bruit (en photons par intervalle de temps),
le bruit (en photons par intervalle de temps), 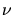 un temps effectif et
un temps effectif et 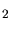 l'écart-type de la gaussienne modèlisant les fluctuations électroniques. La
première partie de la figure
5.4 présente la distribution de charge ADC pour les événements logiciels
aléatoires dans une voie. La fonction ajustée pour la mesure du bruit est superposée
et le
l'écart-type de la gaussienne modèlisant les fluctuations électroniques. La
première partie de la figure
5.4 présente la distribution de charge ADC pour les événements logiciels
aléatoires dans une voie. La fonction ajustée pour la mesure du bruit est superposée
et le 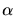 par degré de liberté montre qu'elle décrit très bien la distribution
réelle. L'ajustement se fait par rapport à trois paramètres dont l'un mesure
directement le bruit de fond de ciel en photélectrons par nanoseconde (les deux autres
correspondant à la normalisation et à la translation). La seconde partie de la figure
montre la distribution des valeurs de bruit estimées dans chacune des
voies de la caméra. La valeur moyenne de la gaussienne ajustée sur les canaux pour
lesquels la convergence a été satisfaisante est utilisée comme détermination du
bruit de fond de ciel. C'est une valeur moyenne, à la fois sur la caméra (
par degré de liberté montre qu'elle décrit très bien la distribution
réelle. L'ajustement se fait par rapport à trois paramètres dont l'un mesure
directement le bruit de fond de ciel en photélectrons par nanoseconde (les deux autres
correspondant à la normalisation et à la translation). La seconde partie de la figure
montre la distribution des valeurs de bruit estimées dans chacune des
voies de la caméra. La valeur moyenne de la gaussienne ajustée sur les canaux pour
lesquels la convergence a été satisfaisante est utilisée comme détermination du
bruit de fond de ciel. C'est une valeur moyenne, à la fois sur la caméra (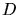 546
pixels) et sur le temps (
546
pixels) et sur le temps (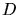 30 minutes).
30 minutes).
Figure 5.4:
Gauche: histogramme de charge des événements logiciels d'une voie ADC avec la
fonction 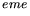 ajustée en trait plein. Droite: distribution du bruit mesuré en
photoélectrons par nanoseconde dans l'ensemble de la caméra et simple gaussienne pour
évaluer la moyenne.
ajustée en trait plein. Droite: distribution du bruit mesuré en
photoélectrons par nanoseconde dans l'ensemble de la caméra et simple gaussienne pour
évaluer la moyenne.
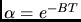 |
Les valeurs typiquement calculés (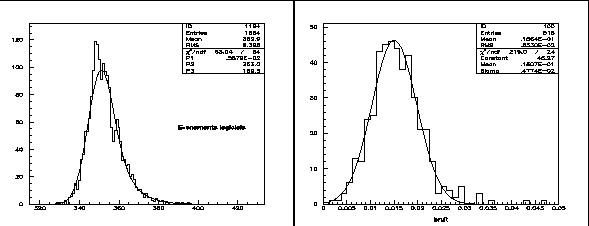 Hz) sont tout à fait en accord avec les
investigations
menées sur le site de Themis par le groupe CELESTE qui a mesuré une moyenne de
Hz) sont tout à fait en accord avec les
investigations
menées sur le site de Themis par le groupe CELESTE qui a mesuré une moyenne de
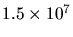 [47], ce qui se traduit dans un pixel de l'imageur CAT
par environ
[47], ce qui se traduit dans un pixel de l'imageur CAT
par environ
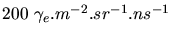 . Les échelles de comptage peuvent
également être utilisées pour estimer le bruit du ciel mais elles ne permettent
qu'une indication de l'ordre de grandeur et de la variabilité. Les taux de comptage sont
trop dépendants des fluctuations électroniques des photomultiplicateurs pour donner
une détermination directe de la valeur absolue.
. Les échelles de comptage peuvent
également être utilisées pour estimer le bruit du ciel mais elles ne permettent
qu'une indication de l'ordre de grandeur et de la variabilité. Les taux de comptage sont
trop dépendants des fluctuations électroniques des photomultiplicateurs pour donner
une détermination directe de la valeur absolue.




Next: Détermination exacte du piedestal
Up: Piedestaux
Previous: Simulation
Contents
Aurelien Barrau
2004-07-01
![]() ns) sont générés tous les dix
événements réels. La valeur exacte du bruit est déterminée par ajustement d'une
fonction
ns) sont générés tous les dix
événements réels. La valeur exacte du bruit est déterminée par ajustement d'une
fonction ![]() (dans le cas où la valeur reste inférieure à quelques photoélectrons
par porte, ce qui est le régime habituel) déterminée de façon "semi-empirique":
(dans le cas où la valeur reste inférieure à quelques photoélectrons
par porte, ce qui est le régime habituel) déterminée de façon "semi-empirique":
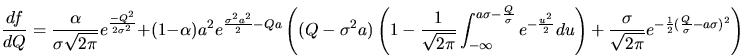 est la charge après déduction de l'effet de fond de ciel,
est la charge après déduction de l'effet de fond de ciel,
 Hz) sont tout à fait en accord avec les
investigations
menées sur le site de Themis par le groupe CELESTE qui a mesuré une moyenne de
Hz) sont tout à fait en accord avec les
investigations
menées sur le site de Themis par le groupe CELESTE qui a mesuré une moyenne de
![]() [47], ce qui se traduit dans un pixel de l'imageur CAT
par environ
[47], ce qui se traduit dans un pixel de l'imageur CAT
par environ
![]() . Les échelles de comptage peuvent
également être utilisées pour estimer le bruit du ciel mais elles ne permettent
qu'une indication de l'ordre de grandeur et de la variabilité. Les taux de comptage sont
trop dépendants des fluctuations électroniques des photomultiplicateurs pour donner
une détermination directe de la valeur absolue.
. Les échelles de comptage peuvent
également être utilisées pour estimer le bruit du ciel mais elles ne permettent
qu'une indication de l'ordre de grandeur et de la variabilité. Les taux de comptage sont
trop dépendants des fluctuations électroniques des photomultiplicateurs pour donner
une détermination directe de la valeur absolue.