Spectre différentiel et comparaisons

Pour construire le spectre d'émission de la source (supposé en loi de puissance), il est nécessaire de tenir compte des effets de faible statistique dans le choix des intervalles d'énergie [72].

Le spectre physique initial peut s'écrire (c'est en tous cas l'hypothèse la plus vraisemblable):

$$\Phi(E)=\Phi_0 \left(\frac{E}{E_0}\right)^{-\gamma}$$

où $\Phi(E)dE$ est le nombre de gammas par unité de surface et par unité de temps dans l'intervalle d'énergie $(E,E+dE)$, $E_0$ une énergie de référence, $\Phi_0$ une constante de normalisation en $cm^{-2}.s^{-1}.TeV^{-1}$ et $\gamma$ l'indice spectral différentiel.

On peut considérer des intervalles en énergie grands devant $\sigma\times E_{moy}$ où $\sigma$ est la résolution de l'ordre de 25% et $E_{moy}$ est l'énergie moyenne de l'intervalle, mais suffisamment petits pour que l'acceptance puisse être développée linéairement comme $A_{\gamma}(E) \approx aE+b$. Le spectre différentiel apparent vaut ainsi:

$$\Phi=\Phi_0\left(\frac{E_0}{E}\right)^{\gamma}(aE+b)$$

et après convolution avec des erreurs gaussiennes (cf annexe A) on obtient en énergie mesurée:

$$\Phi=\Phi_0\left(aE_0e^{\frac{\sigma^2(\gamma-2)^2}{2}}\left(... ...ma^2(\gamma-1)^2}{2}}\left(\frac{E_0}{E}\right)^{\gamma}\right)$$

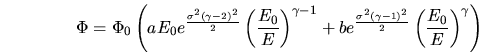Le nombre d'événements de signal dans l'intervalle $(E_1,E_2)$ s'obtient par intégration et multiplication par le temps ( $S=T\int_{E_1}^{E_2}\Phi(E)dE$), soit:

$$S\approx T\Phi_0\left(\frac{aE_0^2}{\gamma-2}e^\frac{\sigma^2... ...gamma-1}- \left(\frac{E_0}{E_2}\right)^{\gamma-1}\right)\right)$$

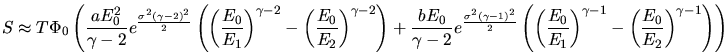où $T$ est le temps d'observation. Pour chaque intervalle (numéroté $i$) on a ainsi $n_i$ événement dans les données "ON-source" et $p_i$ dans les données "OFF-Source". En appelant $\alpha=T_{''ON''}/T_{''OFF''}$, $S_i$ le nombre d'événements de signal attendus et $b_i$ le nombre d'événements de fond attendus, le nombre d'événements "ON-source" attendus est donné par:

$$a_i=\alpha b_i+ S_i$$

Les distributions des nombres effectivement trouvés en "ON" ($n_i$) et "OFF" ($p_i$) sont poissonniennes, on peut donc former une fonction de vraisemblance (dépendant de $\Phi_0$ et de $\gamma$) de la façon suivante:

$$L(\Phi_0,\gamma,b_1,...,b_N)=\Pi_{i=1}^{N}e^{-(S_i+\alpha b_i... ...i+\alpha b_i)^{n_i}}{n_i!}\times e^{-b_i}\frac{b_i^{p_i}}{p_i!}$$

On maximise d'abord cette quantité par rapport aux $b_i$ et on utilise les valeurs $B_i$ obtenues par résolution de l'équation résultante du second degré ( $\frac{\delta ln L}{\delta b_i}=0$):

$$B_i=\frac{1}{2\alpha (\alpha+1)}\left((n_i+p_i)\alpha-S_i(\al... ...sqrt{(n_i+p_i)\alpha-S_i(\alpha+1)+4\alpha(\alpha+1)p_i}\right)$$

Il reste alors à maximiser:

$$ln L'=-(S_i+B_i(\alpha+1))+n_i ln(S_i+\alpha B_i) +p_i ln B_i$$

ce qui peut être entrepris via le programme MINUIT du CERN en utilisant un $\chi ^2$ équivalent de $-2 ln L'$.

Figure 9.2: Spectre différentiel de la nébuleuse du Crabe.

Une autre méthode, ayant le même objectif de correction de l'effet de convolution d'une loi de puissance avec une gaussienne se traduisant par une migration entre les intervalles considérés, a été développée par le groupe de Whipple [73]. C'est une procédure itérative qui consiste à définir une acceptance effective par:

$$A^{eff}_{\gamma}(X)=\frac{e^{\sigma^2 (1-\gamma)^2/2}}{\sigma... ...{2\pi}} \int_{-\infty}^{+\infty}e^{-(x-X_0)^2/2\sigma^2}A(x)dx,$$

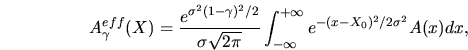avec $X=ln\left(\frac{E}{1~{\rm TeV}}\right)$ et $X_0=X-\sigma^2(\gamma-1)$,

$$A^{eff}_{\gamma}(X)\approx e^{\sigma^2(1-\gamma)^2/2}\left(A(X_0)+\frac{\sigma^2}{2}A''(X_0)+...\right)$$

Cette démarche a également été mise en oeuvre pour vérification. Les résultats sont en parfait accord avec ceux précédemment obtenus.

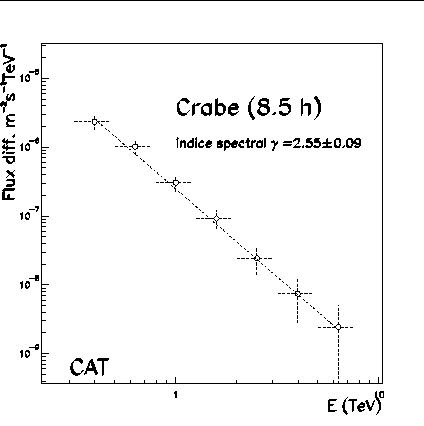
La figure 9.2 donne le flux différentiel du Crabe obtenu entre 400 GeV et 8 TeV en tenant compte de ces effets. Il s'écrit:

$${\bf\Phi = (2.5 \pm 0.2) \times 10^{-7} E^{-2.55 \pm 0.09}~m^{-2}~s^{-1}~TeV^{-1}}$$

où les erreurs sont purement statistiques.

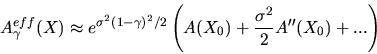
La dernière évaluation du groupe de Whipple [74] (avec des donnés prises à une période différente mais pour l'instant tout porte à croire que le flux du Crabe est constant) est $\Phi = (3.3 \pm 0.2 \pm 0.7) \times 10^{-7} E^{-2.45 \pm 0.08 \pm 0.5}~m^{-2}~s^{-1}~TeV^{-1}$ où les premières erreurs sont statistiques et les secondes systématiques. L'ajustement a été mené entre 500 GeV et 8 TeV et utilise deux méthodes différentes avec des données et des simulations indépendantes entre elles. L'accord avec le flux obtenu par CAT est tout à fait correct dans les erreurs évaluées. La normalisation plus basse dans notre cas vient certainement de la sélection des acquisitions: pour améliorer la statistique, les critères définis à la table 8.2 ont été relachés. Etant donné qu'il n'est pas ici donné de courbe de lumière, la rigoureuse égalité des conditions de prise de données n'est pas indispensable et les coupures sur la variation de qualité du ciel n'ont pas été appliquées. Pour que la comparaison entre les différentes expériences soit pertinente, c'est-à-dire pour que les erreurs statistiques ne masquent pas les éventuels effets systématiques, une nouvelle saison d'observation est nécessaire.

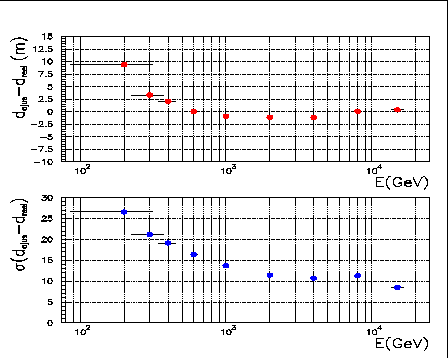La collaboration HEGRA mesure un flux du Crabe de $\Phi \approx 2 \times 10^{-7} E^{-2.66 \pm 0.12}~m^{-2}~s^{-1}~TeV^{-1}$ entre 800 GeV et 10 TeV pour 10 heures de prises de données [90]. La largeur des intervalles d'énergie choisie correspond à peu près au $RMS$ de la résolution supposée. L'indice est légèrement plus grand, et indique certainement une petite systématique entre les expériences (cf partie suivante).

Le groupe de CANGAROO a observé le Crabe à basse élévation (et donc haut seuil) [75] entre 1992 et 1995. Le flux intégral observé s'écrit $\Phi = (8.4 \pm 1.0) \times 10^{-13} \left( \frac{E}{7~TeV} \right)^{-1.53 \pm 0.15}~m^{-2}~s^{-1}$ entre 7 et 50 TeV. L'indice spectral (i.e. 2.53 en différentiel) est bien compatible avec les précédents.

Dans l'attente d'une expérience suffisamment sensible pour autoriser le recouvrement avec des satellites absolument étalonnés, la nébuleuse du Crabe joue donc le rôle de chandelle standard permettant aux différentes équipes de vérifier la convergence de leurs analyses. Cette démarche est décrite plus en détail dans la thèse de Laurent Iacoucci [76].