Limite sur le CIB

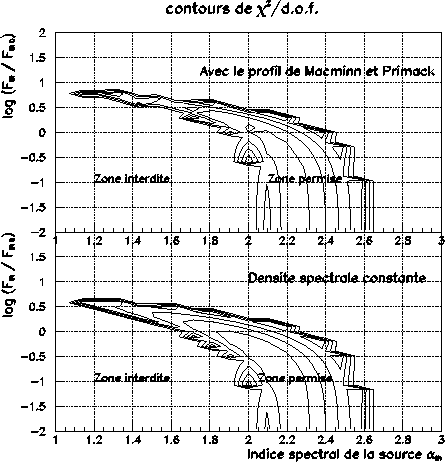
En considérant la forme la plus réaliste de $F_{IR~0}$ (type Macminn et Primack avec un choix arbitraire de normalisation au modèle CDM 1), il apparaît que pour une très faible densité infrarouge ($x<-0.5$), le meilleur $\chi ^2$ conduit naturellement à un indice proche de celui supposé pour la source elle-même. Pour une densité de CIB plus importante ($-0.5<x<0.9$), les valeurs possibles d'indice spectral sont clairement définies. Enfin, les densités élevées ($x>0.9$) sont exclues quel que soit l'indice spectral de la source. Trois types de limites peuvent ainsi être dérivées (cf Figure 13.3):

• si l'indice spectral intrinsèque est celui obtenu en ajustant une loi de puissance sur la partie de basse énergie du spectre expérimental (c'est-à-dire vraisemblablement peu absorbée), une limite supérieure sévère peut être obtenue: $F_{IR}/F_{IR\ 0}\leq1.6$, i.e. $F_{IR}(10\mu{\rm m})\leq1.7\times10^{-6}{\rm ~ergs}.{\rm s}^{-1}.{\rm cm^{-2}}.{\rm sr^{-1}}$ (i.e. 1.7 nW.m$^{-2}$.sr$^{-1}$).

• si l'indice spectral intrinsèque est supposé plus grand que 2, ce qui est suggéré par les modèles de noyaux actifs de galaxie, la limite devient $F_{IR}/F_{IR\ 0}\leq3.0$, i.e. $F_{IR}(10\mu{\rm m})\leq3.3\times10^{-6}{\rm ~ergs}.{\rm s}^{-1}.{\rm cm^{-2}}.{\rm sr^{-1}}$ (i.e. 3.3 nW.m$^{-2}$.sr$^{-1}$).

• si aucune supposition n'est faite sur la source, la limite reste relativement stricte: $F_{IR}/F_{IR\ 0}\leq7.9$, i.e. $F_{IR}(10\mu{\rm m})\leq8.7\times10^{-6}{\rm ~ergs}.{\rm s}^{-1}.{\rm cm^{-2}}.{\rm sr^{-1}}$ (i.e. 8.7 nW.m$^{-2}$.sr$^{-1}$).

Figure 13.3: Limites supérieures obtenues avec les données de CAT pour un indice spectral de la source $\alpha _{th}=2.4$ (pointillés), pour $\alpha _{th}=2$ (tirets) et sans aucune hypothèse sur $\alpha _{th}$ (trait plein). Les cercles sont les limites directes de COBE-DIRBE [204] et les carrés sont issus d'une nouvelle analyse menée à partir des mesures de ce même instrument [199].

Pour un profil constant de $F_{IR~0}$, les niveaux de contour sont très proches et le résultat numérique, en terme de contraintes, demeure essentiellement inchangé en moyennant sur la gamme de sensibilité spectrale.

Il est important de noter que ces limites supérieures sont prudentes pour plusieurs raisons:

• Le modèle de Macminn & Primack n'inclut pas les mécanismes exotiques de production de CIB,
• une éventuelle coupure intrinsèque dans le spectre de la source impliquerait des limites encore plus basses,
• il n'est pas tenu compte d'autres mécanismes d'interaction possibles entre les photons gamma et les constituants du milieu inter-galactique [221].