Origine de l'émission gamma en état bas et des sursauts, discussion

Ce modèle de collisionneur hadronique prédit que les gammas du TeV émis par les blazars fluctuent avec le temps en intensité et en caractéristiques spectrales, même si les propriétés du jet restent constantes. Les particularités exactes des sursauts dépendent d'un très grand nombre de paramètres inconnus. Ils relèvent à la fois du nuage (sa géométrie, sa distribution de densité surfacique, sa vitesse, sa trajectoire...) et du jet (son angle d'ouverture $\theta_{jet}$, son orientation par rapport à l'observateur, sa composition exacte, sa distribution spectrale d'énergie en fonction de la distance latérale et longitudinale...). Un comportement général peut néanmoins être étudié sous certaines hypothèses [134] [135] [136].

Figure 12.2: Paramètres géométriques du modèle.

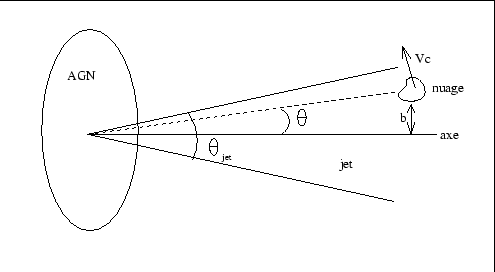
Soient un jet de particules et un nuage cible séparés par une distance $R$. Soient $b$ et $\theta$ le paramètre d'impact et l'angle relatif (cf figure 12.2). L'essentiel des photons gamma observés proviennent d'une zone de paramètre d'impact inférieur à $b_c\approx RE_0/E_{\gamma}<R\theta_{jet}$ compte-tenu du comportement exponentiel de la section efficace précédemment explicité. Le nombre de nuages avec $b<b_c$ dans la zone d'émission de raies larges est $N_{BLR}E_0^2/4E_{\gamma}^2$, où $N_{BLR}$ est le nombre total de nuages dans la zone en question. Une émission quasi-constante a lieu si ce nombre est grand, c'est-à-dire si $E_{\gamma}\ll E_{crit}=N_{BLR}^{1/2}E_0/2\approx C_{BLR}^{1/2}R_{16}r_{12}$ TeV, où $C_{BLR}$ est la fraction du ciel vue de l'AGN couverte par des nuages, $R_{16}=R/10^{16}$ cm et $r_{12}=r_c/10^{12}$ cm ($r_c$ désignant le rayon typique d'un nuage). Dans ce cas, le jet produit un flux quasi-continu de gammas s'écrivant

$$\frac{dF_{\gamma}}{dE_{\gamma}}\approx C_{BLR}\overline{N}_p\sigma_{in}IA_{\gamma}^{-\alpha}.$$

Un sursaut se produit lorsqu'un nuage croise la ligne de visée à une relativement petite distance. Si le rayon du nuage est supérieur au paramètre d'impact critique, le nuage obstrue la ligne de visée et le flux de gammas d'énergie $E_{\gamma}>(R/r_c)E_0\approx1.6R_{16}/r_{12}$ TeV augmente avec une intensité maximum de

$$\frac{dF_{\gamma}}{dE_{\gamma}}\approx{N}_p\sigma_{in}IA_{\gamma}^{-\alpha},$$

où $N_p$ désigne la densité surfacique moyenne du nuage. Le rapport de l'intensité maximale du sursaut à l'intensité quasi-continue en état bas est donc $N_p/C_{BLR}\overline{N}_p$. Or, le facteur $C_{BLR}$ peut être estimé par le rapport des photons Ly$_\alpha$ émis par les nuages aux photons produits par le continuum central (hydrogène ionisé). La valeur est voisine de $C_{BLR}\approx0.1$.

Lors des récentes observations de Mrk501, le flux maximum détecté par CAT était environ 7 fois le flux de la nébuleuse du Crabe. Ce qui signifie que le flux détecté lors du sursaut le plus important est environ 90 fois supérieur au flux quasi-constant de Mrk 501 en état bas [137]. D'où l'on peut déduire un rapport $N_p/\overline{N}_p\approx 9$ entre les densités surfaciques des nuages responsables des états hauts et bas. C'est, dans le cadre de ce modèle, une mesure de l'inhomogénéité de la concentration de matière dans les nuages au voisinage l'AGN.

La durée de l'émission au TeV dans de tels sursauts est de l'ordre du temps nécessaire au nuage pour croiser la ligne de visée. $V_c$ étant la vitesse du nuage, celui-ci s'écrit:

$$\delta T\approx 2r_c/V_c \approx 1.7\times10^3r_{12}R_{16}^{1/2}M_8^{-1/2} {\rm s}.$$

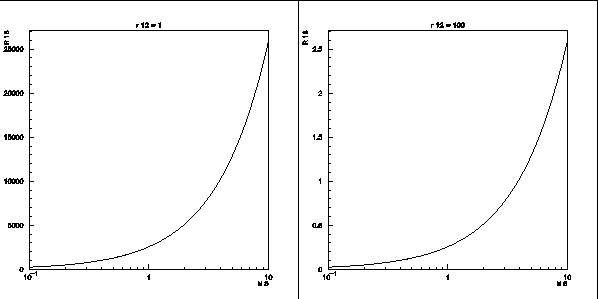
Les observations de CAT mettent en évidence des temps typiques de l'ordre d'une journée pour les sursauts bien définis (c'est-à-dire montée et descente). On peut en déduire la distance entre les nuages de matière à l'origine des sursauts et le trou noir comme une fonction de la masse de ce dernier pour différentes valeurs raisonnables du rayon du nuage. Le résultat est donné sur la figure 12.3.

Figure 12.3: Distance du nuage à l'AGN (en unités de $10^{16}$ cm) en fonction de la masse du trou noir (en unités de $10^8$ masses solaires) selon les résultats de CAT, pour des rayons de nuage $r_ {12}$ (en unités de $10^{12}$ cm) de 1 et 100.

Le modèle prédit également un durcissement du spectre durant les sursauts qui n'est pas incompatible avec les mesures de CAT.

Un dernier point fondamental est lié à la production corrélative de rayonnements d'autres longueurs d'onde. La chaîne de production $pp \rightarrow \pi \rightarrow \mu \rightarrow e$ consécutive à la collision du jet avec un nuage enrichit soudainement le jet en électrons. A cause des lois d'échelle de Feynman, leur spectre différentiel est proportionnel à celui des gammas: $dn_e/dE \approx 0.5 dn_{\gamma}/dE_{\gamma}$. Leur refroidissement par effet Compton-inverse et synchrotron produit des photons optiques, X et gammas mous retardés dans le temps. Le pic d'émission synchrotron des électrons avec un facteur de Lorentz $\Gamma_e$ traversant un champ magnétique perpendiculaire $H(G)$ se déplaçant avec un facteur Doppler $\delta=(1-\beta cos\theta)/\Gamma_H$ le long du jet se trouve à une énergie $E_{\gamma}\approx 5\times10^{-12}H\Gamma_e\delta$ keV [138]. Les électrons perdent 50% de leur énergie initiale en un temps

$$\tau \approx 5\times 10^8\Gamma_e^{-1}H^{-2}\delta {\rm s}\ap... ... 1.2\times 10^3H^{-3/2}E_{\gamma}^{-1/2}\delta^{-1/2} {\rm ~s}.$$

Les résultats du satellite XTE donnent des mesures du flux de Mrk 501 entre 2 et 10 keV [139]. L'évaluation de la fonction de corrélation CAT-XTE en fonction du décalage temporel (cf modèles SSC) entre les deux séries de mesures montre que celui-ci ne doit pas être largement supérieur à une journée. On peut alors en déduire une limite inférieure sur $H$ en fonction de $\delta$, donnée à la figure 12.4.

Figure 12.4: Limite inférieure du champ magnétique H (en gauss) en fonction du facteur Doppler $\delta$ suivant les résultats CAT-XTE: $H>7.6\times 10^{-2}\delta ^{-1/3}$.