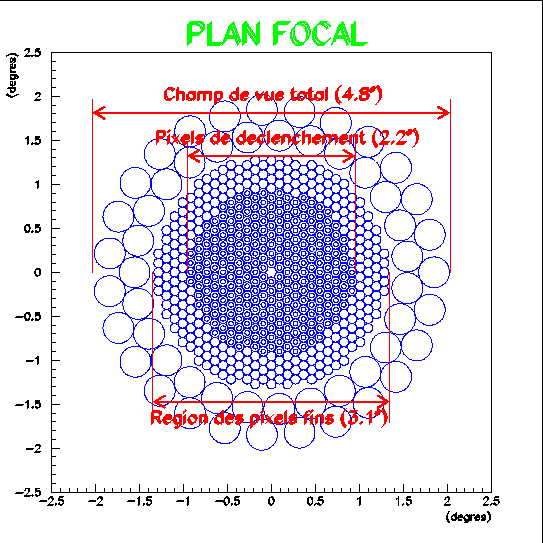
 cm pour les 546 tubes internes) afin d'avoir des
pixels très fins dans la caméra (indispensables pour la reconstruction des
paramètres physiques des gammas de basse énergie),
cm pour les 546 tubes internes) afin d'avoir des
pixels très fins dans la caméra (indispensables pour la reconstruction des
paramètres physiques des gammas de basse énergie),
 ns)
afin de tirer parti du synchronisme de la lumière Tcherenkov
ns)
afin de tirer parti du synchronisme de la lumière Tcherenkov
Le télescope CAT pouvant être considéré comme un instrument de deuxième génération, supposé exploiter et améliorer des techniques connues, le choix des détecteurs s'est naturellement porté vers les photomultiplicateurs qui demeurent aujourd'hui sans équivalent. Il n'est pas exclu que la prochaine génération, ayant recours à une électronique différente, puisse exploiter la bonne efficacité quantique et la grande linéarité des détecteurs à faible gain (les photodiodes hybrides - HPD - en particulier). Dans notre cas, les caractéristiques requises sont essentiellement:
 cm pour les 546 tubes internes) afin d'avoir des
pixels très fins dans la caméra (indispensables pour la reconstruction des
paramètres physiques des gammas de basse énergie),
cm pour les 546 tubes internes) afin d'avoir des
pixels très fins dans la caméra (indispensables pour la reconstruction des
paramètres physiques des gammas de basse énergie),
 ns)
afin de tirer parti du synchronisme de la lumière Tcherenkov
ns)
afin de tirer parti du synchronisme de la lumière Tcherenkov
La combinaison de ces critères réduit la palette des choix possibles au point que
seul un modèle du constructeur Hamamatsu (avec une photocathode et une fenêtre
d'entrée
adaptées à l'ultra-violet) peut simultanément les satisfaire. Directement dérivé du
standard R1635, c'est le modèle R3878 qui a été testé très en détail et
choisi pour l'expérience. Son diamètre est de 11 mm et celui de la surface active
de la photocathode de 8 mm. La collection de lumière renormalisée à la
surface a
été évaluée à l'aide de différents diaphragmes (cf tableau 4.3)
et à
différentes valeurs de haute tension.
L'efficacité quantique (c'est-à-dire la probabilité qu'un photon incident sur la photocathode engendre un électron) du modèle choisi avec verre spécial UV est typiquement représentée à la figure 4.6. Ces valeurs, issues d'un calcul mené en fonction des caractéristiques physiques du matériau cathodique, ont été confirmées par les mesures du constructeur.
La résolution du photoélectron unique est importante à plusieurs niveaux. Dans
un premier temps, elle permet une détermination simple du gain du
photomultiplicateur. Celui-ci est déterminé au cours d'une acquisition
dédiée réalisée une à
trois fois par mois. La conversion du nombre de canaux ADC (charge mesurée par le
convertisseur analogique-numérique) en photoélectrons est directement issue de
l'ajustement d'une gaussienne au spectre du photoélectron unique. Ceci doit être
mesuré à gain élevé (au moins ![]() )
pour bien distinguer ce spectre du piedestal. La séparation claire du pic est
indispensable pour la procédure de mesure du gain ultérieurement décrite.
La description détaillée de la méthode est donnée dans le
chapitre 3 Suivi et évolution des performances.
Dans un second temps, la précision de la reconstruction du nombre de photons
touchant le photomultiplicateur à partir de la charge mesurée est bien-sûr
liée à la précision avec laquelle on peut évaluer le nombre de
photoélectrons délivrés. La largeur de la gaussienne ajustant le pic du
photoélectron, normalisée à la charge, est utilisée comme indicateur standard
de la qualité du photomultiplicateur du point de vue de sa résolution. La forme
du spectre est donnée sur la figure 4.7.
)
pour bien distinguer ce spectre du piedestal. La séparation claire du pic est
indispensable pour la procédure de mesure du gain ultérieurement décrite.
La description détaillée de la méthode est donnée dans le
chapitre 3 Suivi et évolution des performances.
Dans un second temps, la précision de la reconstruction du nombre de photons
touchant le photomultiplicateur à partir de la charge mesurée est bien-sûr
liée à la précision avec laquelle on peut évaluer le nombre de
photoélectrons délivrés. La largeur de la gaussienne ajustant le pic du
photoélectron, normalisée à la charge, est utilisée comme indicateur standard
de la qualité du photomultiplicateur du point de vue de sa résolution. La forme
du spectre est donnée sur la figure 4.7.
Nous avons mesuré ce rapport ![]() sur un échantillon de 225
photomultiplicateurs et la distribution des valeurs obtenues est donnée sur la
figure 4.8. La valeur moyenne est de 0.43, ce qui est l'ordre de grandeur de ce que
l'on peut obtenir de meilleur pour ce type de tubes sans demander une sélection
draconienne de la production. La dispersion n'est que de 0.04, ce qui garantit une
bonne homogénéité de la caméra du point de vue de sa résolution. Aucun
photomultiplicateur utilisé ne présente un rapport supérieur à 0.65. Par
ailleurs, l'indépendance de cette caractéristique vis-à-vis de la haute
tension (dès lors que le pic est clairement visible) a été vérifiée à
mieux que 10 %.
sur un échantillon de 225
photomultiplicateurs et la distribution des valeurs obtenues est donnée sur la
figure 4.8. La valeur moyenne est de 0.43, ce qui est l'ordre de grandeur de ce que
l'on peut obtenir de meilleur pour ce type de tubes sans demander une sélection
draconienne de la production. La dispersion n'est que de 0.04, ce qui garantit une
bonne homogénéité de la caméra du point de vue de sa résolution. Aucun
photomultiplicateur utilisé ne présente un rapport supérieur à 0.65. Par
ailleurs, l'indépendance de cette caractéristique vis-à-vis de la haute
tension (dès lors que le pic est clairement visible) a été vérifiée à
mieux que 10 %.
Les caractéristiques temporelles du photomultiplicateur sont essentielles à deux
niveaux: d'une part pour le déclenchement et d'autre part pour
la lecture de la charge délivrée. Dans le premier cas, c'est avant tout le
temps de montée de l'impulsion qui va jouer et permettre un seuil très faible
tirant parti, autant que faire se peut, du synchronisme des photons Tcherenkov.
Dans le second cas, c'est surtout la largeur du signal qui va permettre un temps
d'intégration court (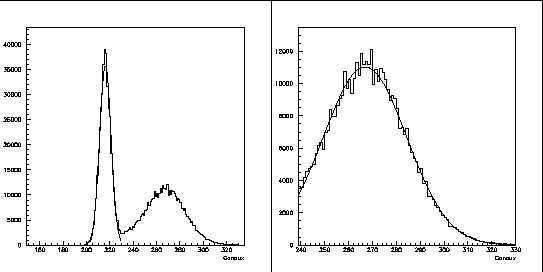 ns). La figure 4.9 présente une impulsion
typique des photomultiplicateurs utilisés.
La largeur est dûe aux fluctuations de temps de collection
des électrons dans l'espace cathode - première dynode d'une part et dans
les étages successifs du multiplicateur d'autre part. Les fluctuations des
différents étages peuvent être caractérisées par des réponses propres
d'écart-type respectifs
ns). La figure 4.9 présente une impulsion
typique des photomultiplicateurs utilisés.
La largeur est dûe aux fluctuations de temps de collection
des électrons dans l'espace cathode - première dynode d'une part et dans
les étages successifs du multiplicateur d'autre part. Les fluctuations des
différents étages peuvent être caractérisées par des réponses propres
d'écart-type respectifs
![]() ,
,
![]() , ... ,
, ... ,
![]() . En toute rigueur, les événements aléatoires qui se produisent
à chaque étage ne sont pas indépendants mais si l'on fait l'hypothèse très
raisonnable [42] que la densité de probabilité d'arrivée des
électrons sur l'anode est représentée par
. En toute rigueur, les événements aléatoires qui se produisent
à chaque étage ne sont pas indépendants mais si l'on fait l'hypothèse très
raisonnable [42] que la densité de probabilité d'arrivée des
électrons sur l'anode est représentée par
![]() ,
la variance
,
la variance 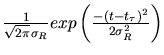 de la réponse impulsionnelle peut être évaluée
comme la somme des variances de chaque étage. Les étages de rang supérieur à
2 étant identiques, on obtient:
de la réponse impulsionnelle peut être évaluée
comme la somme des variances de chaque étage. Les étages de rang supérieur à
2 étant identiques, on obtient:
![]() ,
avec une largeur à mi-hauteur
,
avec une largeur à mi-hauteur
![]() . L'impulsion représentée ici est une réponse au
photoélectron unique, ce qui minimise sa largeur puisque le terme
. L'impulsion représentée ici est une réponse au
photoélectron unique, ce qui minimise sa largeur puisque le terme
![]() n'intervient plus (pas de fluctuations dans l'espace cathode-première dynode).
Outre le choix de la répartition des tensions dans le pont diviseur, la rapidité
est obtenue par une géométrie bien adaptée à la minimisation des
phénomènes électrodynamiques dans l'espace de collection du multiplicateur (en
particulier la création d'un courant HF dû à l'oscillation d'électrons autour
de la grille). D'autre part, l'adapation (généralement imparfaite) des
dernières électrodes à la ligne de transmission a été soignée de
façon à ne pas dégrader la forme de l'impulsion.
n'intervient plus (pas de fluctuations dans l'espace cathode-première dynode).
Outre le choix de la répartition des tensions dans le pont diviseur, la rapidité
est obtenue par une géométrie bien adaptée à la minimisation des
phénomènes électrodynamiques dans l'espace de collection du multiplicateur (en
particulier la création d'un courant HF dû à l'oscillation d'électrons autour
de la grille). D'autre part, l'adapation (généralement imparfaite) des
dernières électrodes à la ligne de transmission a été soignée de
façon à ne pas dégrader la forme de l'impulsion.
Dans notre cas, la fraction de signal intégrée dans la porte de 13 ns a été mesurée à 85% en moyenne. De plus, il a été vérifié que cette proportion ne dépend pas de l'amplitude du signal.
Le courant noir des photomultiplicateurs est une donnée importante [41]. Le comportement du taux de comptage en fonction
d'un seuil de discrimination ne suit pas une loi de Poisson.
Ceci est essentiellement dû à la
présence d'impulsions secondaires (after pulses) causées par des
remontées d'ions dans le tube qui induisent une production importante d'électrons
entre les dynodes. Ces impulsions secondaires sont importantes dans la mesure où
elles peuvent dépasser le seuil habituel choisi pour le déclenchement (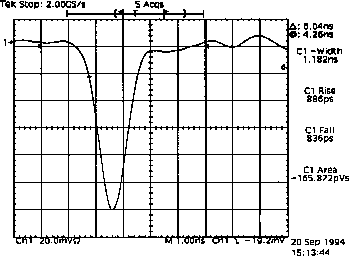 photoélectrons). Leur fréquence dans l'obscurité est négligeable (de l'ordre
de quelques Hertz) mais elle peut devenir importante lorsque le photomultiplicateur
est soumis à un éclairement aléatoire élevé (en l'occurence le bruit de
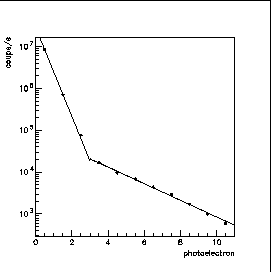
fond de ciel). La courbe donnant le taux de comptage du photomultiplicateur en
fonction du seuil de discrimination choisi est invariante de forme selon
l'intensité de la lumière: elle se transforme par simple homothétie. Il suffit donc de
déterminer la forme générale (donnée sur la figure 4.10) et d'
imposer une limite sur le courant noir à un seuil arbitraire
pour majorer le comptage résultant sur le fond de ciel.
La figure 4.10 montre
par ailleurs qu'en fixant le seuil individuel d'un photomultiplicateur à 3
photoélectrons (cf 2.3 Electronique de déclenchement et d'acquisition
), on parvient à une réduction du taux de
fond de ciel d'un facteur
photoélectrons). Leur fréquence dans l'obscurité est négligeable (de l'ordre
de quelques Hertz) mais elle peut devenir importante lorsque le photomultiplicateur
est soumis à un éclairement aléatoire élevé (en l'occurence le bruit de
fond de ciel). La courbe donnant le taux de comptage du photomultiplicateur en
fonction du seuil de discrimination choisi est invariante de forme selon
l'intensité de la lumière: elle se transforme par simple homothétie. Il suffit donc de
déterminer la forme générale (donnée sur la figure 4.10) et d'
imposer une limite sur le courant noir à un seuil arbitraire
pour majorer le comptage résultant sur le fond de ciel.
La figure 4.10 montre
par ailleurs qu'en fixant le seuil individuel d'un photomultiplicateur à 3
photoélectrons (cf 2.3 Electronique de déclenchement et d'acquisition
), on parvient à une réduction du taux de
fond de ciel d'un facteur ![]() environ.
environ.
Le courant d'obscurité dépend beaucoup de la température puisqu'il est directement lié à l'agitation thermique des électrons. Les mesures ont été effectuées au laboratoire dans des conditions moins favorables qu'au cours de l'expérience. Cette caractéristique dépend également du temps de mise sous tension du photomultiplicateur qui élimine progressivement les ions éventuellement présents dans le tube par interaction avec les électrons accélérés. Les fréquences enregistrées en fonction du temps de mise sous tension montrent qu'après une demi-heure de chauffe le courant noir se stabilise.
La figure 4.11 présente la distribution des hautes tensions
pour une valeur de gain donnée
(![]() ) sur l'échantillon de 225 photomultiplicateurs testés. Les
tensions sont ajustées de façon à uniformiser le gain sur la caméra. Il en
résulte une dispersion de ces dernières
dont la conséquence est une dispersion des temps de
transit des photomuliplicateurs. La variation de ceux-ci en
) sur l'échantillon de 225 photomultiplicateurs testés. Les
tensions sont ajustées de façon à uniformiser le gain sur la caméra. Il en
résulte une dispersion de ces dernières
dont la conséquence est une dispersion des temps de
transit des photomuliplicateurs. La variation de ceux-ci en
 (où
(où ![]() est la haute tension appliquée) équivaut, d'après les tests
effectués avec un laser à impulsions rapides, à un décalage de 600 ps par
100 V. L'électronique de déclenchement étant fondée sur une coïncidence
très brève entre les signaux des photomultiplicateurs (
est la haute tension appliquée) équivaut, d'après les tests
effectués avec un laser à impulsions rapides, à un décalage de 600 ps par
100 V. L'électronique de déclenchement étant fondée sur une coïncidence
très brève entre les signaux des photomultiplicateurs (![]() ns), les tubes
participant au déclenchement ont été triés. La dispersion de tension obtenue
pour ces 288 photomultiplicateurs se traduit par une dispersion de temps d'environ
300 ps, négligeable devant les caractéristiques intrinsèques de la lumière
Tcherenkov et l'asynchronisme du miroir. Elle est donc sans conséquence sur
l'efficacité de déclenchement. Pour les autres photomultiplicateurs, le
décalage temporel d'arrivée des signaux est quasiment sans importance
compte tenu de la méthode de calcul du gain (cf chapitre 3
Evolution et suivi des performances).
ns), les tubes
participant au déclenchement ont été triés. La dispersion de tension obtenue
pour ces 288 photomultiplicateurs se traduit par une dispersion de temps d'environ
300 ps, négligeable devant les caractéristiques intrinsèques de la lumière
Tcherenkov et l'asynchronisme du miroir. Elle est donc sans conséquence sur
l'efficacité de déclenchement. Pour les autres photomultiplicateurs, le
décalage temporel d'arrivée des signaux est quasiment sans importance
compte tenu de la méthode de calcul du gain (cf chapitre 3
Evolution et suivi des performances).
Il est faut également vérifier que la relation charge-amplitude des impulsions du photomultiplicateur est linéaire. Ceci permet de s'assurer qu'il y a bien une correspondance bi-univoque simple entre le seuil de déclenchement fixé en mV et la charge mesurée en pC. La distribution obtenue (figure 4.12) présente un très bon coefficient de corrélation linéaire de 0.94.
L'efficacité de collection d'un photomultiplicateur est la probabilité qu'un
électron émis au niveau de la photocathode soit recueilli par la première
dynode et donne donc lieu à l'émission d'un photoélectron au niveau de
l'anode.
Compte-tenu du pont diviseur choisi dans la base (deux fois la résistance moyenne entre la
photocathode et la première dynode), la tension du premier étage avoisine
160 Volts à 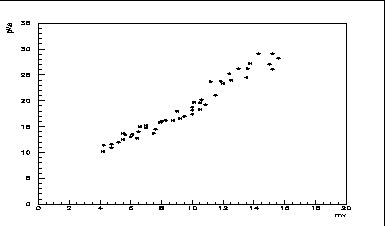 . L'efficacité de collection intégrée sur la
photocathode vaut alors pratiquement 90% selon les données constructeur.
Elle est dans notre cas meilleure
puisque seule la partie centrale est utilisée (cf 2.2.3 cônes de Winston).
. L'efficacité de collection intégrée sur la
photocathode vaut alors pratiquement 90% selon les données constructeur.
Elle est dans notre cas meilleure
puisque seule la partie centrale est utilisée (cf 2.2.3 cônes de Winston).
Nous avons mesuré, à l'aide de différents diaphragmes, que
|