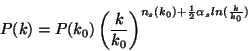Bien que non encore découverte, la supersymétrie (SUSY) est sans aucun doute la meilleure
extension du modèle standard de la physique des particules. Elle
fournit un cadre général pour comprendre l'origine de la différence entre les
bosons et les fermions et donne des directions très prometteuses pour résoudre le
problème de la hiérarchie (i.e. l'instabilité de l'échelle électrofaible
vis-à-vis des corrections radiatives). En supersymétrie globale, les
spinneurs générateurs ![]() satisfont à
satisfont à
![]() [113]. Si
l'on veut s'intéresser à la supersymétrie locale (i.e. à la
supergravité), cette condition doit être assouplie et les
[113]. Si
l'on veut s'intéresser à la supersymétrie locale (i.e. à la
supergravité), cette condition doit être assouplie et les ![]() deviennent fonction des
coordonnées
deviennent fonction des
coordonnées ![]() . De nouveaux termes, proportionnels à
. De nouveaux termes, proportionnels à
![]() , doivent
être "neutralisés" par l'introduction d'une particule de spin 3/2, appelée
gravitino, à la manière des bosons vecteurs introduits en théories de jauge.
Le gravitino fait partie d'un multiplet
, doivent
être "neutralisés" par l'introduction d'une particule de spin 3/2, appelée
gravitino, à la manière des bosons vecteurs introduits en théories de jauge.
Le gravitino fait partie d'un multiplet ![]() qui contient le graviton, de spin 2 (voir
[114] pour une revue introductive), et, dans la phase brisée de la
supersymétrie, des effets de type super-Higgs le rendent massif par absorption des
fermions de Nambu-Goldstone associés à la brisure de SUSY.
qui contient le graviton, de spin 2 (voir
[114] pour une revue introductive), et, dans la phase brisée de la
supersymétrie, des effets de type super-Higgs le rendent massif par absorption des
fermions de Nambu-Goldstone associés à la brisure de SUSY.
Il est connu depuis longtemps que si le gravitino est instable des contraintes
sévères existent sur sa masse afin d'éviter une surproduction d'entropie
[115]:
![]() TeV. D'un autre coté, s'il est stable, sa
masse doit satisfaire
TeV. D'un autre coté, s'il est stable, sa
masse doit satisfaire
![]() keV [116] afin de garder une
densité de gravitinos inférieure à celle de l'Univers (
keV [116] afin de garder une
densité de gravitinos inférieure à celle de l'Univers (
![]() ).
En dépit de la gigantesque dilution induite, l'inflation ne résoud pas
complètement ces problèmes car des gravitinos doivent être à nouveau produits
par diffusion lors du processus de reheating à la fin de celle-ci
[117,118,119,120,121,122,123]. Etant donné que le nombre de
gravitinos ainsi produits est proportionnel à la température de reheating
).
En dépit de la gigantesque dilution induite, l'inflation ne résoud pas
complètement ces problèmes car des gravitinos doivent être à nouveau produits
par diffusion lors du processus de reheating à la fin de celle-ci
[117,118,119,120,121,122,123]. Etant donné que le nombre de
gravitinos ainsi produits est proportionnel à la température de reheating
![]() , il est possible de lier l'échelle d'énergie de l'inflation avec la
requête que les gravitinos ne soient pas sur-produits. Nous avons ainsi récemment montré
[112] que les expériences CMB pourraient permettre d'exclure la supergravité. En effet,
la cosmologie de précision est entrée, ces dernières années, dans une nouvelle ère
(voir [124] par
exemple) grâce à Maxima, BOOMERanG, ACBAR,
DASI, CBI, VSA, ARCHEOPS & WMAP. L'ensemble de ces mesures a conforté le
paradigme inflationnaire en montrant des fluctuations gaussiennes, invariantes
d'échelle et une densité très proche de la densité critique. Le point important
ici est que la polarisation a, pour la première fois, été mise en évidence
[125,126]. Pour l'instant, seul le mode E (pair) a été vu et le mode B
(impair) reste à découvrir. Ce dernier est particulièrement important parce qu'il
signerait les ondes gravitationnelles primordiales.
De très gros efforts sont actuellement consacrés à la recherche de ce mode B et
nous avons établi qu'une détection contredirait la supersymétrie locale parce
qu'elle requiérerait une échelle d'inflation (
, il est possible de lier l'échelle d'énergie de l'inflation avec la
requête que les gravitinos ne soient pas sur-produits. Nous avons ainsi récemment montré
[112] que les expériences CMB pourraient permettre d'exclure la supergravité. En effet,
la cosmologie de précision est entrée, ces dernières années, dans une nouvelle ère
(voir [124] par
exemple) grâce à Maxima, BOOMERanG, ACBAR,
DASI, CBI, VSA, ARCHEOPS & WMAP. L'ensemble de ces mesures a conforté le
paradigme inflationnaire en montrant des fluctuations gaussiennes, invariantes
d'échelle et une densité très proche de la densité critique. Le point important
ici est que la polarisation a, pour la première fois, été mise en évidence
[125,126]. Pour l'instant, seul le mode E (pair) a été vu et le mode B
(impair) reste à découvrir. Ce dernier est particulièrement important parce qu'il
signerait les ondes gravitationnelles primordiales.
De très gros efforts sont actuellement consacrés à la recherche de ce mode B et
nous avons établi qu'une détection contredirait la supersymétrie locale parce
qu'elle requiérerait une échelle d'inflation (![]() GeV) si haute qu'elle
entrerait clairement en conflit avec la limite supérieure venant des gravitinos
(
GeV) si haute qu'elle
entrerait clairement en conflit avec la limite supérieure venant des gravitinos
(![]() GeV en étant très conservatif).
GeV en étant très conservatif).
Le lien avec les petits trous noirs vient de ce que leur mise en évidence pourrait,
elle aussi, être liée à l'échelle d'énergie de l'inflation. En fait, les PBH
ne peuvent se former qu'avec des masses très voisines de la masse de Hubble à
l'instant considéré (pour des raisons évidentes de causalité). Il s'ensuit que
si de tels trous noirs étaient détectés, i.e. si leurs masses actuelles
étaient de l'ordre de
![]() g, la masse de l'horizon dans l'Univers
primordial devrait avoir présenté des valeurs de cet ordre de grandeur. Ce qui
signifie que l'échelle d'énergie de reheating ne pourrait avoir été trop
basse. L'idée consiste donc à étudier les contraintes qui pourraient être
obtenues en supposant que des expériences futures (en particulier AMS, bien-sûr)
détectent un flux d'antideutérons dû à des trous noirs primordiaux. On peut
d'abord noter qu'il serait assez simple de discriminer ce signal d'un signal de
neutralinos en annihilation pour la simple raison que l'espace des paramètres SUSY
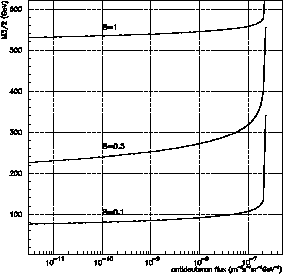
correspondant aura été exploré par le LHC. La figure 3.4 présente, à
gauche, les
températures de reheating possibles en fonction de la densité totale de trous
noirs primordiaux pour 4 flux différents de
g, la masse de l'horizon dans l'Univers
primordial devrait avoir présenté des valeurs de cet ordre de grandeur. Ce qui
signifie que l'échelle d'énergie de reheating ne pourrait avoir été trop
basse. L'idée consiste donc à étudier les contraintes qui pourraient être
obtenues en supposant que des expériences futures (en particulier AMS, bien-sûr)
détectent un flux d'antideutérons dû à des trous noirs primordiaux. On peut
d'abord noter qu'il serait assez simple de discriminer ce signal d'un signal de
neutralinos en annihilation pour la simple raison que l'espace des paramètres SUSY
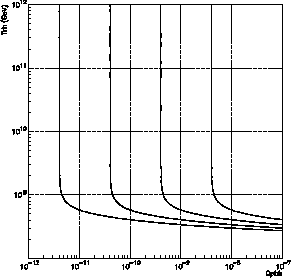
correspondant aura été exploré par le LHC. La figure 3.4 présente, à
gauche, les
températures de reheating possibles en fonction de la densité totale de trous
noirs primordiaux pour 4 flux différents de ![]() . Si l'on tient compte de la
limite supérieure obtenue sur
. Si l'on tient compte de la
limite supérieure obtenue sur ![]() dans les chapitres précédents, cela
se traduit par une limite inférieure sur
dans les chapitres précédents, cela
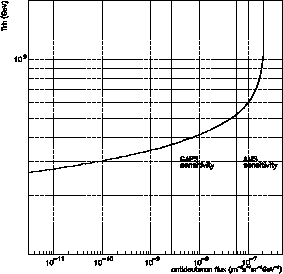
se traduit par une limite inférieure sur ![]() en fonction du flux de
en fonction du flux de ![]() ,
présentée sur la droite de la figure avec la sensibilité de deux expériences.
,
présentée sur la droite de la figure avec la sensibilité de deux expériences.
|
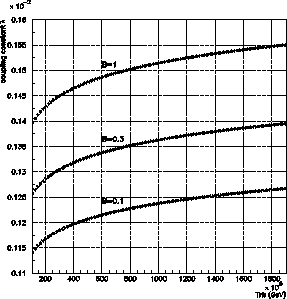
Il est intéressant de tenir alors compte du "problème" des gravitinos et de
déduire de ces limites sur la température de reheating une contrainte sur la
masse de ces particules. Il faut résoudre une équation de type Boltzmann pour les
gravitinos [127]:
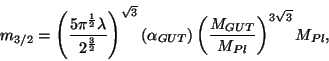
|
Cette voie est encore à creuser. En particulier, deux points importants devraient
être explorés plus en détails. Le premier est relatif au modèle particulier
de supergravité choisi. Nous avons ici raisonné essentiellement dans le cadre mSUGRA
où la masse du gravitino est, par construction, attendue autour de l'échelle
électrofaible (disons entre 100 GeV et 1 TeV). Il serait intéressant de
considérer plus en profondeur les alternatives et, en particulier, les modèles de
type GMSB (brisure de supersymétrie à médiation de jauge) qui sont beaucoup
discutés en ce moment. Leur intérêt essentiel réside en ce qu'ils permettent
une supression naturelle du taux de changement de saveur dans les courants neutres
grâce à une basse échelle d'énergie. Dans ces cas, les gravitinos sont les
particules supersymétriques les plus légères (LSP) avec des masses comprises entre
100 keV et 10 MeV. La contrainte sur ![]() est alors encore plus stricte puisqu'il
sagit cette fois d'avoir une densité de gravitinos inférieure à la densité
totale (les gravitinos sont ici stables si la R-parité est conservée) :
est alors encore plus stricte puisqu'il
sagit cette fois d'avoir une densité de gravitinos inférieure à la densité
totale (les gravitinos sont ici stables si la R-parité est conservée) :
![]() GeV selon la masse. Une étude globale de la validité des limites
dans les différents modèles supersymétriques serait une extension intéressante du
travail réalisé.
GeV selon la masse. Une étude globale de la validité des limites
dans les différents modèles supersymétriques serait une extension intéressante du
travail réalisé.
Il serait aussi important de voir comment ces limites s'accordent avec les modèles faisant
intervenir des transitions des phase du premier ordre [129]. Dans ces
derniers, les trous noirs résultent de la collision de bulles de "vrai vide"
dans un fond de "faux vide" et des trous noirs peuvent de former avec des masses
dont la valeur dépend de la théorie de champ sous-jacente utilisée
[5].
Un autre point important concerne les modèles d'inflation. De façon à concilier
inflation à haute échelle d'énergie et supersymétrie locale, des modèles de
type inflation thermique ont été développés [130]. L'idée de base est de
tenir compte de ce que, au cours de l'évolution cosmologique, la dilution s'effectue
de façon approximativement isentropique
![]() . Si donc une grande
quantité d'entropie (par exemple via un champ scalaire qui domine la radiation à une
certaine époque) est libérée dans l'Univers avant que les gravitinos ou autres
champs de moduli ne se désintègrent, le problème peut être, dans une large
mesure, évité. On retrouve cette idée dans le modèle du curvaton [131].
Il serait utile d'étudier plus en détail dans quelle mesure une détection de
trous noirs primordiaux corrélée à une éventuelle détection de gravitinos
légers auprès d'autres expériences pourrait favoriser un tel scénario
cosmologique. Une question similaire se pose d'ailleurs pour le mode B dans le CMB.
. Si donc une grande
quantité d'entropie (par exemple via un champ scalaire qui domine la radiation à une
certaine époque) est libérée dans l'Univers avant que les gravitinos ou autres
champs de moduli ne se désintègrent, le problème peut être, dans une large
mesure, évité. On retrouve cette idée dans le modèle du curvaton [131].
Il serait utile d'étudier plus en détail dans quelle mesure une détection de
trous noirs primordiaux corrélée à une éventuelle détection de gravitinos
légers auprès d'autres expériences pourrait favoriser un tel scénario
cosmologique. Une question similaire se pose d'ailleurs pour le mode B dans le CMB.
Enfin, un certain nombre de modèles d'inflation actuellement très discutés
prédisent un running spectral index ![]() , autrement dit supposent que le
, autrement dit supposent que le ![]() n'est
pas invariant d'échelle. Le spectre est alors généralement paramétrisé sous
la forme
n'est
pas invariant d'échelle. Le spectre est alors généralement paramétrisé sous
la forme