Rayons cosmiques galactiques : processus de spallation [12]

Pour rechercher les trous noirs primordiaux éventuellement présents dans l'Univers et soumis au processus d'évaporation précédemment mentionné, les antiprotons cosmiques constituent une sonde particulièrement favorable : le rapport $\bar{p}/p$, de l'ordre de $10^{-5}$ pour les processus conventionnels, assure une faible contamination due aux mécanismes de spallation. Une composante ténue, issue de l'évaporation de trous noirs, pourrait donc être aisément mise en évidence. Il convient néanmoins d'étudier en premier lieu la composante secondaire, produite par les phénomènes physiques habituels, qui constitue dans cette approche un bruit de fond dont la connaissance est indispensable.

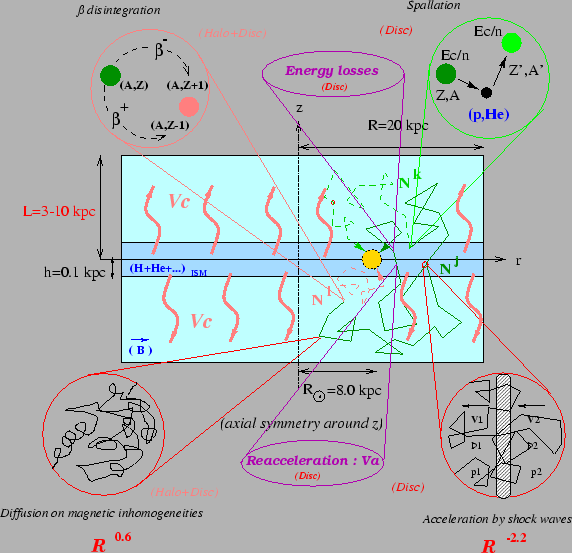
L'élément fondamental pour décrire une population de rayons cosmiques galactiques est un modèle fiable de diffusion. Nous utilisons ici l'approche "à deux zones" initiée au LAPTH. Cette approche est mathématiquement équivalente à la fameuse "boîte qui fuit" utilisée durant des décénnies. Elle présente néanmoins trois avantages substantiels qui ont motivé notre choix : d'abord, c'est une démarche plus physique puisqu'elle ne suppose pas l'homogénéité de la "boîte qui fuit" (elle-même en contradiction avec l'idée même de diffusion), ensuite les paramètres qui y sont utilisés peuvent être directement liés à des observables physiques, enfin c'est l'unique façon de prendre en compte les termes sources primaires qui seront utilisés ultérieurement. La figure 1.1 présente les ingrédients fondamentaux du modèle. Les détails techniques et les longues formules analytiques sont exposés dans [12,13]. Nous donnons ici les idées essentielles.

Figure: Modélisation de la galaxie, dessin David Maurin. Le disque gris foncé représente la matière et le disque gris clair représente la halo diffusif.

Figure: Flux mesurés de protons (haut) et d'hélium (bas) par AMS [14] (croix) et BESS [15] (cercles) avec le meilleur ajustement.

La géométrie de la galaxie est supposée cylindrique avec une extension $R=20$ kpc, la matière (les étoiles et le gaz) étant confinée dans un disque fin d'épaisseur $2h=200$ pc. Les cinq paramètres de ce modèle sont $K_0$, $\delta$ (décrivant la normalisation et l'indice spectral du coefficient de diffusion $K(E)=K_0 \beta {\rm R}^{\delta}$ où R est la rigidité), la demi-hauteur du halo $L$, la vitesse de convection $V_c$ et la vélocité d'Alfvén $V_a$. Ils sont laissés libres dans une certaine gamme qui est déterminée par la compatibilité des flux calculés avec les flux mesurés pour les noyaux cosmiques [13].

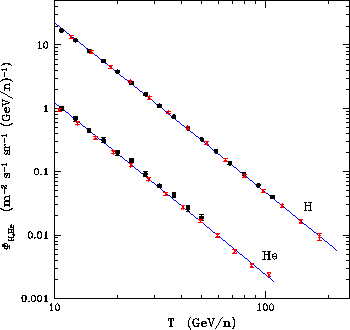
Le terme source de cette étude est constitué des flux de protons et d'Hélium, tels que mesurés par les expériences AMS et BESS [14,15] et présentés sur la figure 1.2. Le meilleur ajustement (présenté sur la figure) est : $\Phi=13.249 E^{-2.72}$ où $E$ représente l'énergie cinétique par nucléon et $\Phi$ le flux différentiel. Les incertitudes sur les paramètres n'excèdent pas 1% et sont donc sans conséquence.

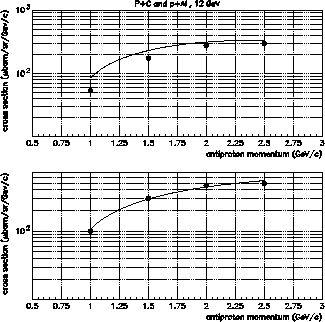
Le terme dominant pour le calcul du flux d'antiprotons secondaires vient des interactions $p-p$ (l'un étant un rayon cosmique et l'autre un noyau d'hydrogène interstellaire). Comme la plupart des études sur les rayons cosmiques, nous utilisons ici la paramétrisation de Tan & Ng [16] pour la section efficace et écrivons le terme source :

$$q_{\bar{p}}^{sec}(r,E) \; = \; {\displaystyle \int_{Threshol... ...\, n_{H} \, \left\{ 4 \, \pi \, \Phi_{p}(r,E') \right\} \, dE'$$ (1.18)

où $n_H$ représente la densité d'hydrogène dans le milieu insterstellaire et $\Phi_{p}$ le flux différentiel de protons. Il est néanmoins apparu que la prise en compte unique de la composante "proton" était insuffisante et qu'il était important d'inclure également les noyaux d'hélium. Moins que pour la normalisation du spectre, cela est fondamental pour etudier en détail sa forme aux basses énergies. Après avoir utilisé un certain nombre de paramétrisations analytiques ou de modèles empiriques [17], nous avons opté pour une simulation Monte-Carlo [18]. Ce code, DTUNUC, est une implémentation du modèle dual partonique fondé sur l'approche de Gribov-Glauber qui traite les diffusions faiblement inélastiques selon la phénoménologie de Regge et les diffusions fortement inélastiques selon les méthodes de QCD perturbative (en utilisant les librairies CERN habituelles : PHOJET, PYTHIA, LEPTO, etc.). La figure 1.3 montre, à gauche, les vérifications entreprises sur la précision du programme et la qualité de l'accord entre les mesures et les calculs. La partie droite présente les contributions intégrées des différentes composantes cosmiques au flux d'antiprotons.

Figure: Gauche : Sections efficaces de production d'antiprotons pour p+C (haut) et p+Al (bas) pour une énergie cinétique de 12 GeV dans le laboratoire, mesurées (points) et calculées par DTUNUC (traits). Droite : Sections efficaces calculées pour les 3 contributions importantes (He-He, p-He et He-p)

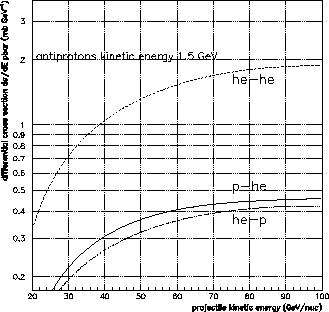
Une fois créés, les antiprotons peuvent interagir avec le milieu interstellaire de différentes façons. D'abord, il peuvent interagir élastiquement. Les sections efficaces étant très piquées en avant, les pertes d'énergie correspondantes sont négligeables. Ensuite, ils peuvent s'annihiler. Ce processus est dominant à basse énergie et les sections efficaces sont données par [19]. Enfin, ils peuvent subir des interactions inélastiques non-annihilantes. Dans de tels cas, il survivent à la collision mais perdent de l'énergie. Le terme source correspondant s'écrit :

$$q_{\bar{p}}^{ter}(r , E_{\bar{p}}) = {\displaystyle \int_{E... ... \, n_{H} \, v_{\bar{p}} \; N^{\bar{p}}(r , E_{\bar{p}}) \;\;.$$

Avec une section efficace différentielle donnée par $d \sigma_{\rm\bar{p} H \to \bar{p} X}/dE_{\bar{\rm p}} = \sigma^{\bar{p}p}_{non-ann}/T'_{\bar{\rm p}}$ où $T'_{\bar{\rm p}}$ représente l'énergie cinétique de l'antiproton, la production tertiaire s'écrit:

$$q_{\bar{p}}^{ter}(r , E) \; = \; 4 \, \pi \, n_{H} \left\{ {... ...\bar{p}p}_{non-ann}(E) \, \Phi_{\bar{p}}(r , E) \right\} \;\;.$$

La prise en compte de ce phénomène, qui avait été omis dans les premières études [20], est très importante pour la description du flux sous le GeV puisqu'il s'agit d'une redistribution des énergies.

Figure: Gauche : Flux calculés (les deux courbes correspondent aux erreurs "astrophysiques") et points expérimentaux. Droite : Flux calculés (les deux courbes correspondent aux erreurs "nucléaires") et points expérimentaux.

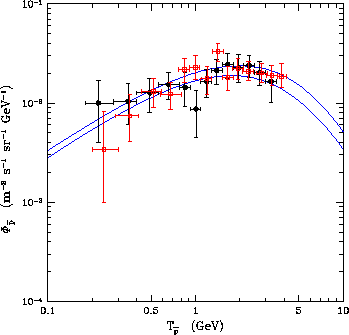
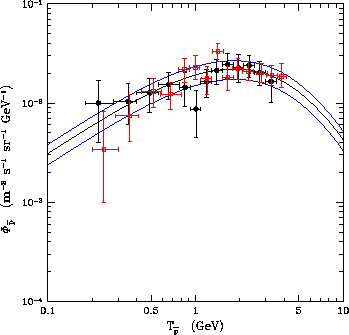
La figure 1.4 présente les flux ainsi obtenus. Dans la partie gauche, les valeurs des sections efficaces nucléaires sont fixées à leurs moyennes et seules figurent les incertitudes liées aux paramètres astrophysiques du modèle. La gamme de variation de ces derniers est déterminée en demandant que le modèle reproduise correctement les flux B/C (rapport de l'abondance du Bohr au Carbone) [13]. La partie droite présente, au contraire, les incertitudes nucléaires seules. Il est intéressant de noter que, contrairement à ce qui aurait pu être attendu, ce sont les erreurs associées aux processus subatomiques qui dominent. Les autres incertitudes (flux primaires, densité d'hydrogène galactique, modulation solaire, etc.) sont nettement sous-dominantes [12].

La conclusion essentielle de cette étude consiste à montrer que, dans un modèle physique dont les paramètres sont fixés par d'autres données, les flux d'antiprotons sont très bien expliqués. Les points expérimentaux sont en excellent accord avec les calculs lorsque la composante tertiaire et la diffusion énergétique sont prises en compte. C'est une bonne nouvelle pour la maîtrise du bruit de fond et la fiabilité de la démarche. C'est une nettement moins bonne nouvelle pour la recherche de nouvelle physique puisque l'ensemble du spectre est expliqué sans recourir à des objets exotiques (en particulier à basse énergie, là ou un excès a longtemps été envisagé). Cela permet néanmoins de mettre d'excellentes limites supérieures (puisque, précisément, il n'y a "plus de place" pour d'autres processus).

Peut-on pousser l'ambition jusqu'à considérer qu'une excellente mesure astrophysique du flux d'antiprotons donnerait une mesure des sections efficaces nucléaires? Je pense que c'est encore une boutade et sans doute très prématuré. Mais, dans un futur un peu plus lointain...