



suivant: Gammas primaires
monter: Comment traquer les trous
précédent: Rayons cosmiques galactiques : processus
Table des matières
Le flux d'antiprotons issus de processus "conventionnels" étant maintenant
connu, nous nous proposons ici d'étudier le flux d'antiprotons issus d'une éventuelle
population de trous noirs primordiaux (PBH) dans notre galaxie.
Le spectre de Hawking donnant le flux différentiel de particules par unité de temps
s'écrit, par degré de liberté, pour une énergie 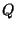 :
:
où 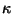 représente la gravité de surface du trou noir,
représente la gravité de surface du trou noir,
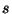 le spin de l'entité émise et
le spin de l'entité émise et 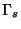 la
probabilité d'absorption correspondante. La charge et le moment angulaire du trou noir ont été
omis dans cette expression, dans la mesure où ces derniers s'annulent dès les
premiers instants de l'évaporation [22].
Dès que la température du trou noir est supérieure à l'échelle de
confinement de QCD, des quarks et des gluons sont émis [23,24] (et non pas des hadrons comme
cela fut supposé initialement). Cela rend l'écriture du spectre plus complexe :
la
probabilité d'absorption correspondante. La charge et le moment angulaire du trou noir ont été
omis dans cette expression, dans la mesure où ces derniers s'annulent dès les
premiers instants de l'évaporation [22].
Dès que la température du trou noir est supérieure à l'échelle de
confinement de QCD, des quarks et des gluons sont émis [23,24] (et non pas des hadrons comme
cela fut supposé initialement). Cela rend l'écriture du spectre plus complexe :
où 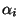 représente le nombre de degrés de liberté,
représente le nombre de degrés de liberté, 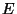 est l'énergie de
l'antiproton et
est l'énergie de
l'antiproton et
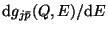 est la fonction de fragmentation
différentielle normalisée, c'est-à-dire le nombre d'antiprotons d'énergie
comprise entre
est la fonction de fragmentation
différentielle normalisée, c'est-à-dire le nombre d'antiprotons d'énergie
comprise entre 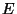 et
et 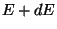 créés par un parton de type
créés par un parton de type 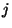 et d'énergie
et d'énergie 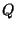 .
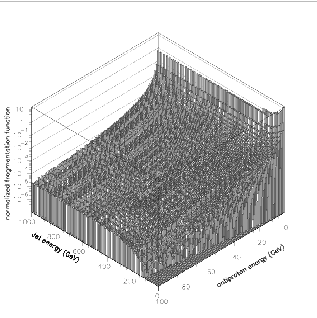
Pour calculer ces fonctions de fragmentation (la figure 1.5, à gauche, présente un
exemple pour un quark u), nous avons utilisé la simulation
Monte-Carlo PYTHIA [102] fondée sur le modèle des cordes classiques de
Lund. De plus, pour le calcul des
.
Pour calculer ces fonctions de fragmentation (la figure 1.5, à gauche, présente un
exemple pour un quark u), nous avons utilisé la simulation
Monte-Carlo PYTHIA [102] fondée sur le modèle des cordes classiques de
Lund. De plus, pour le calcul des 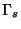 , donnés par
, donnés par
où 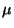 est la masse de la particule émise,
la section efficace
est la masse de la particule émise,
la section efficace
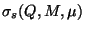 a été évaluée exactement en utilisant
les calculs numériques de D. Page (J.H. MacGibbon communication privée) et non pas
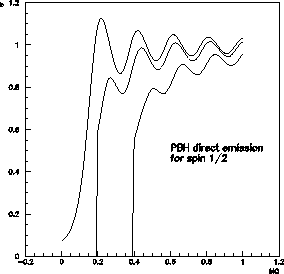
un prenant la limite ultra-relativiste usuellement supposée. La figure 1.5
présente, à droite, ce comportement pseudo oscillant qui change les résultats de
quelques pourcents.
a été évaluée exactement en utilisant
les calculs numériques de D. Page (J.H. MacGibbon communication privée) et non pas
un prenant la limite ultra-relativiste usuellement supposée. La figure 1.5
présente, à droite, ce comportement pseudo oscillant qui change les résultats de
quelques pourcents.
Figure:
Gauche : Fonction de fragmentation d'un quark u en antiprotons,
en fonction de l'énergie du jet et de l'énergie cinétique de l'antiproton
émergeant. Droite : section efficace (normalisée à la limite optique)
d'absorption d'une particule par un trou noir en fonction du produit de la masse du
trou noir par l'énergie de la particule (en unité de Planck) pour trois valeurs de
masse (de bas en haut :
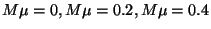 ).
).
|
|
Afin de calculer le spectre d'antiprotons pour une densité locale de PBH fixée, le
nombre
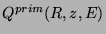 d'antiprotons emis avec une énergie cinétique comprise entre
d'antiprotons emis avec une énergie cinétique comprise entre
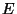 et
et 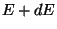 par unité de volume et de temps doit être évalué. Il est
proportionnel au nombre
par unité de volume et de temps doit être évalué. Il est
proportionnel au nombre 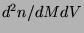 de PBH par unité de masse et de volume et au flux
individuel
de PBH par unité de masse et de volume et au flux
individuel
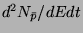 émis par un PBH, soit
émis par un PBH, soit
où 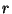 et
et 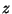 sont les coordonnées cylindriques décrivant la position dans la
galaxie. Comme la physique de l'évaporation ne dépend pas de la densité
numérique, on peut écrire
sont les coordonnées cylindriques décrivant la position dans la
galaxie. Comme la physique de l'évaporation ne dépend pas de la densité
numérique, on peut écrire
avec
où
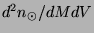 représente le spectre de masse local, par unité de
volume.
Les trous noirs primordiaux doivent présenter une distribution spatiale similaire à
celle des particules de matière noire froide (CDM). Hélas, la forme du halo CDM est
encore très mal connue (voir, par exemple, [26] et références incluses)
et nous utilisons la description générale :
représente le spectre de masse local, par unité de
volume.
Les trous noirs primordiaux doivent présenter une distribution spatiale similaire à
celle des particules de matière noire froide (CDM). Hélas, la forme du halo CDM est
encore très mal connue (voir, par exemple, [26] et références incluses)
et nous utilisons la description générale :
où les valeurs numériques de 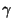 ,
, 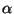 et
et 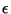 sont données dans
[27] (le profil isotherme classique s'obtient avec
sont données dans
[27] (le profil isotherme classique s'obtient avec 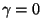 ,
, 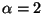 et
et
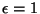 ).
).
La détermination du spectre de masse des trous noirs primordiaux aujourd'hui (i.e. en
tenant compte de ce qu'ils se sont formés il y a 13.8 Myr) demande,
en principe, la connaissance du spectre initial et de la loi d'évolution temporelle de
la masse de chaque PBH. Le premier point a été étudié par Carr [28]
et conduit à supposer
pour un spectre de puissance primordial invariant d'échelle de type Harrison-Zeldovitch. La dérivation de cette
distribution est très complexe et relativement modèle dépendante. Néanmoins, nous
verrons par la suite qu'elle ne joue pratiquement aucun rôle dans l'ensemble des
résultats obtenus. En revanche, la prise en compte du terme d'évolution est
primordiale. Celui-ci s'obtient simplement par intégration du spectre de Hawking
multiplié par l'énergie, conduisant à :
où 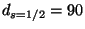 et
et 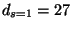 (pour
(pour
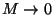 ) tiennent compte du nombre de degrés de liberté
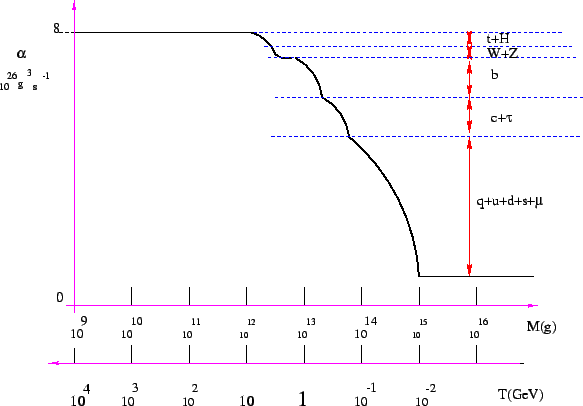
accessibles dans le modèle standard. La figure 1.6 présente le terme
) tiennent compte du nombre de degrés de liberté
accessibles dans le modèle standard. La figure 1.6 présente le terme
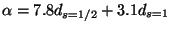 en fonction de la masse : plus le trou noir est léger, plus il
est chaud, plus grand est le nombre de champs qui lui sont accessibles, i.e. dont la
masse est inférieure à la température du PBH. Si l'on fait l'approximation
en fonction de la masse : plus le trou noir est léger, plus il
est chaud, plus grand est le nombre de champs qui lui sont accessibles, i.e. dont la
masse est inférieure à la température du PBH. Si l'on fait l'approximation
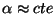 , ce qui est correct pour les petites masses, on peut écire :
, ce qui est correct pour les petites masses, on peut écire :
Et avec
le spectre aujourd'hui peut s'écrire:
où
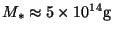 est la masse initiale d'un PBH qui termine sa
vie aujourd'hui.
est la masse initiale d'un PBH qui termine sa
vie aujourd'hui.
Figure:
Terme "quasi-constant" du taux de perte de masse en fonction de la
masse du trou noir. Le trou noir peut émettre des particules de plus en plus massives au
fur et à mesure que la température augmente. Dessin G. Boudoul.
|
|
La figure 1.7 présente, à gauche, le flux d'antiprotons obtenu après
convolution avec le spectre de masse des PBH (avant propagation).
Comme attendu,
les trous noirs dont la masse est supérieure à 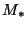 contribuent peu
compte-tenu de ce que leur température est très faible. Les trous noirs de
masse très petite contribuent également de façon sous-dominante, en
dépit de leur température élevée, à cause de leur faible densité
numérique (effet
contribuent peu
compte-tenu de ce que leur température est très faible. Les trous noirs de
masse très petite contribuent également de façon sous-dominante, en
dépit de leur température élevée, à cause de leur faible densité
numérique (effet 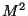 dans le spectre de masse qui traduit physiquement
l'accélération de l'évaporation). C'est donc en fait la gamme de masse
dans le spectre de masse qui traduit physiquement
l'accélération de l'évaporation). C'est donc en fait la gamme de masse
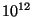 g -
g - 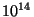 g qui est essentiellement sondée à l'aide des
antiprotons cosmiques. La partie droite de cette figure présente l'effet d'une
coupure dans le spectre de masse initial due à la taille finie du rayon de Hubble
à la fin de l'inflation. Seuls les trous noirs formés à l'issue de cette
phase étant effectivement à prendre en compte (compte-tenu de la dilution
exponentielle de ceux formés avant celle-ci), une éventuelle masse de l'horizon
trop grande peut conduire à une réduction drastique de la population de PBH.
Avec la masse de Hubble à un instant
g qui est essentiellement sondée à l'aide des
antiprotons cosmiques. La partie droite de cette figure présente l'effet d'une
coupure dans le spectre de masse initial due à la taille finie du rayon de Hubble
à la fin de l'inflation. Seuls les trous noirs formés à l'issue de cette
phase étant effectivement à prendre en compte (compte-tenu de la dilution
exponentielle de ceux formés avant celle-ci), une éventuelle masse de l'horizon
trop grande peut conduire à une réduction drastique de la population de PBH.
Avec la masse de Hubble à un instant 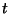 donnée
donnée
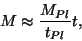
où
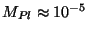 g et
g et
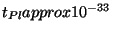 s sont la masse et le
temps de Planck.
et le moment
s sont la masse et le
temps de Planck.
et le moment 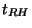 de la fin de l'inflation lié à la
température de reheating
de la fin de l'inflation lié à la
température de reheating 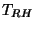 par
par
où 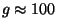 est le nombre de degrés de liberté dans l'Univers
primordial, on peut évaluer la conséquence d'une valeur de
est le nombre de degrés de liberté dans l'Univers
primordial, on peut évaluer la conséquence d'une valeur de 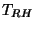 finie sur
le spectre de masse. La température critique est de l'ordre de
finie sur
le spectre de masse. La température critique est de l'ordre de
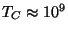 GeV : au-dessus de celle-ci, la distribution des trous noirs n'est pas
significativement affectée dans la zone d'intérêt; en dessous de celle-ci le
spectre est exponentiellement supprimé (ce point sera étudié plus en détails dans les
chapitres suivants).
L'effet d'une possible photosphère QCD au voisinage de l'horizon du trou noir a
également été considéré. Il a, en effet, été suggéré
[29] qu'au-delà d'une certaine température la radiation de Hawking
devrait interagir avec elle-même et constituer un plasma de quarks et de gluons
qui affecterait les
processus vus à l'infini. Une analyse numérique a été menée [30]
en résolvant l'équation de Boltzmann pour laquelle les conditions aux limites
sont libres à l'infini et fixées par le spectre de Hawking à
GeV : au-dessus de celle-ci, la distribution des trous noirs n'est pas
significativement affectée dans la zone d'intérêt; en dessous de celle-ci le
spectre est exponentiellement supprimé (ce point sera étudié plus en détails dans les
chapitres suivants).
L'effet d'une possible photosphère QCD au voisinage de l'horizon du trou noir a
également été considéré. Il a, en effet, été suggéré
[29] qu'au-delà d'une certaine température la radiation de Hawking
devrait interagir avec elle-même et constituer un plasma de quarks et de gluons
qui affecterait les
processus vus à l'infini. Une analyse numérique a été menée [30]
en résolvant l'équation de Boltzmann pour laquelle les conditions aux limites
sont libres à l'infini et fixées par le spectre de Hawking à 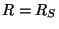 . Il en
résulte une réduction drastique du flux à haute énergie mais un effet
très limité entre 100 MeV et 1 GeV, c'est-à-dire dans la zone d'intérêt
pour la détection.
. Il en
résulte une réduction drastique du flux à haute énergie mais un effet
très limité entre 100 MeV et 1 GeV, c'est-à-dire dans la zone d'intérêt
pour la détection.
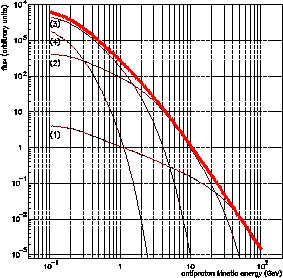
Figure:
Gauche : Flux d'antiprotons primaires avant propagation
(unités arbitraires). La courbe (1) correspond à
![$M\in[M_{Pl},10^{12}{\rm g}]$](img226.png) , la courbe (2) à
, la courbe (2) à
![$M\in[10^{12}{\rm g},10^{13}{\rm g}]$](img227.png) , la courbe (3) à
, la courbe (3) à
![$M\in[10^{13}{\rm
g},5\cdot10^{13}{\rm g}]$](img228.png) , la courbe (4) à
, la courbe (4) à
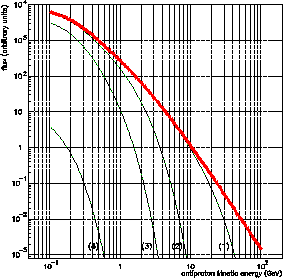
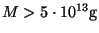 et la ligne épaisse est le spectre total. Droite : évolution en fonction de
la températeure de reheating. La courbe (1) correspond à
et la ligne épaisse est le spectre total. Droite : évolution en fonction de
la températeure de reheating. La courbe (1) correspond à
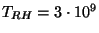 GeV, la courbe (2) à
GeV, la courbe (2) à
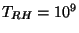 GeV, la courbe (3) à
GeV, la courbe (3) à
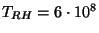 GeV, la courbe (4)
à
GeV, la courbe (4)
à
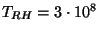 GeV et la ligne épaisse est le spectre sans coupure.
GeV et la ligne épaisse est le spectre sans coupure.
|
|
Pour calculer le flux d'antiprotons induits par les trous noirs primordiaux au niveau
de la Terre et le comparer avec les données expérimentales, il faut commencer
par considerer les antiprotons secondaires. Quand les pertes d'énergie sont
négligées, la densité 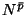 s'écrit (en état stationnaire) :
s'écrit (en état stationnaire) :
ce qui représente simplement une équation de diffusion ou le 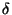 de
Dirac s'applique aux processus ayant lieu dans le disque galactique supposé
mince.
de
Dirac s'applique aux processus ayant lieu dans le disque galactique supposé
mince.
La symétrie cylindrique du problème permet de développer les quantités en
séries de Bessel:
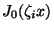 (
(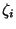 est le
est le 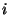 eme zéro de
eme zéro de
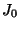 et
et
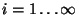 ).
La solution de l'équation (1.19) peut alors s'écrire
).
La solution de l'équation (1.19) peut alors s'écrire
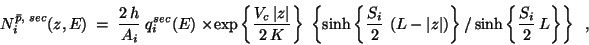 |
(1.20) |
où les quantités 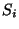 et
et 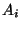 sont définies par:
sont définies par:
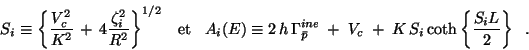 |
(1.21) |
En ce qui concerne les primaires (i.e. venant de PBH), à
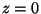 où les flux sont mesurés, la densité s'écrit
où les flux sont mesurés, la densité s'écrit
où
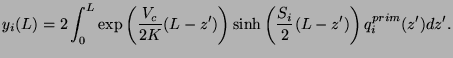 |
|
|
(1.22) |
Le spectre est affecté par des pertes d'énergie quand les 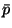 interagissent avec la matière interstellaire et par des gains d'énergie quand
des processus de réaccélération prennent naissance. Ces variations sont
décrites par l'équation intégro-différentielle:
interagissent avec la matière interstellaire et par des gains d'énergie quand
des processus de réaccélération prennent naissance. Ces variations sont
décrites par l'équation intégro-différentielle:
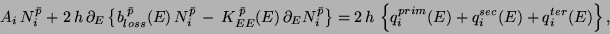 |
(1.23) |
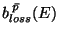 représentant les pertes d'énergie.
Le terme source
représentant les pertes d'énergie.
Le terme source
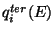 conduit à la composante dite tertiaire qui
résulte des interactions inélastiques non annihilantes.
La résolution de cette équation est détaillée dans [12] et
conduit à :
conduit à la composante dite tertiaire qui
résulte des interactions inélastiques non annihilantes.
La résolution de cette équation est détaillée dans [12] et
conduit à :
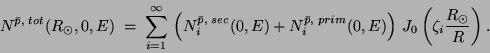 |
(1.24) |
où 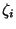 est le
est le 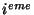 zéro de la fonction de Bessel.
Il convient de prendre garde à ce que le halo de matière noire s'étend bien au
delà du halo diffusif mais on peut montrer (cf appendice B de [21])
que la contribution des sources situées à
zéro de la fonction de Bessel.
Il convient de prendre garde à ce que le halo de matière noire s'étend bien au
delà du halo diffusif mais on peut montrer (cf appendice B de [21])
que la contribution des sources situées à 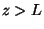 est négligeable. Enfin,
différents types de profils de halo de matière noire ont été testés et la
solution isotherme (i.e. conduisant au plus petit flux) a été choisie
pour demeurer "conservatif".
est négligeable. Enfin,
différents types de profils de halo de matière noire ont été testés et la
solution isotherme (i.e. conduisant au plus petit flux) a été choisie
pour demeurer "conservatif".
Figure:
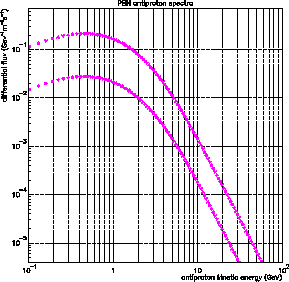
Gauche : Flux d'antiprotons primaires après propagation
et modulation solaire (au niveau de l'atmosphère donc) pour
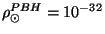 g cm
g cm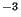 correspondant aux modèles astrophysiques
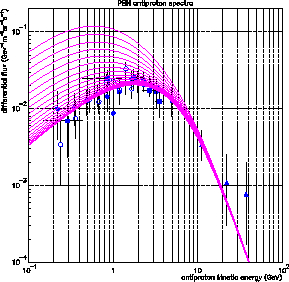
extrêmes. Droite : Données expérimentales de BESS95 (cercles pleins), BESS98
(cercles), CAPRICE (triangles) et AMS (carrés) superposées aux flux calculés
pour des densités de PBH entre
correspondant aux modèles astrophysiques
extrêmes. Droite : Données expérimentales de BESS95 (cercles pleins), BESS98
(cercles), CAPRICE (triangles) et AMS (carrés) superposées aux flux calculés
pour des densités de PBH entre
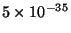 g cm
g cm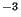 (courbe basse) et
(courbe basse) et
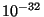 g cm
g cm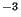 .
.
|
|
Après utilisation de ce modèle de propagation, il faut tenir compte de l'effet
local du champ magnétique solaire. Celui-ci est traité dans l'approximation du
champ de force [31]. Tous les paramètres astrophysiques décrivant la
diffusion sont alors variés dans la gamme autorisée par l'étude des noyaux.
La figure 1.8 présente, à gauche, les flux obtenus au sommet de
l'atmosphère pour les deux cas extrêmes de paramètres diffusifs. Les
incertitudes "astrophysiques" s'élèvent donc à environ un ordre de grandeur.
Cette valeur est nettement plus importante que pour les antiprotons secondaires, ce
qui peut se comprendre de façon intuitive: dans le modèle le plus simple,
l'évolution des secondaires est entièrement dictée par le rapport 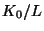 alors que les primaires, dont les sources ne sont pas uniquement dans le disque
galactique mais aussi dans le halo, dependent directement de
alors que les primaires, dont les sources ne sont pas uniquement dans le disque
galactique mais aussi dans le halo, dependent directement de 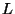 . Ce paramètre
n'étant pas contraint par l'étude exhaustive des noyaux jusqu'à Z=30
[31], il s'ensuit une dégénérescence sur les spectres primaires.
. Ce paramètre
n'étant pas contraint par l'étude exhaustive des noyaux jusqu'à Z=30
[31], il s'ensuit une dégénérescence sur les spectres primaires.
Figure:
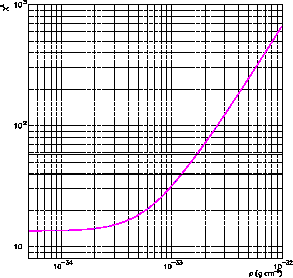
Gauche : 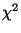 entre les données expérimentales et les
flux théoriques en fonction de la densité locale de PBH pour un halo
magnétique d'épaisseur 3 kpc. Les droites horizontales correspondent à des
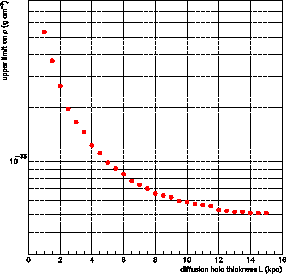
niveaux de confiance de 95% et 99%. Droite : Limite supérieure sur la densité
de PBH en fonction de la taille du halo magnétique
entre les données expérimentales et les
flux théoriques en fonction de la densité locale de PBH pour un halo
magnétique d'épaisseur 3 kpc. Les droites horizontales correspondent à des
niveaux de confiance de 95% et 99%. Droite : Limite supérieure sur la densité
de PBH en fonction de la taille du halo magnétique 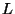 .
.
|
|
La partie droite de la figure 1.8 présente les flux d'antiprotons primaires
(pour un modèle astrophysique moyen) en fonction de la densité de trous noirs
primordiaux. Clairement, la courbe la plus basse (i.e. où seuls sont
présents des secondaires) est en adéquation satisfaisante avec les données.
Il s'agit donc de dériver une limite supérieure. Pour ce faire nous
définissons un 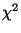 généralisé qui tient compte des incertitudes
expérimentales disymétriques:
généralisé qui tient compte des incertitudes
expérimentales disymétriques:
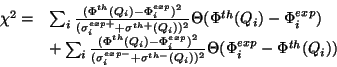
où 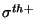 et
et 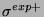 (
(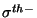 et
et 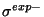 ) sont les
erreurs théoriques et expérimentales positives (négatives). Une limite
supérieure sur la densité de PBH est calculée pour chaque valeur de taille
du halo diffusif (
) sont les
erreurs théoriques et expérimentales positives (négatives). Une limite
supérieure sur la densité de PBH est calculée pour chaque valeur de taille
du halo diffusif (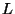 ). Les incertitudes théoriques tiennent compte à la fois
des aspects astrophysiques et nucléaires (
). Les incertitudes théoriques tiennent compte à la fois
des aspects astrophysiques et nucléaires (
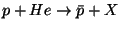 et
et
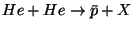 ). La figure 1.9 présente, à gauche,
l'évolution du
). La figure 1.9 présente, à gauche,
l'évolution du 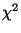 en fonction de la densité pour
en fonction de la densité pour 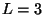 kpc et les lignes
horizontales correspondent à des niveaux de confiance de 63% et 99%. La partie
droite de cette figure donne la limite supérieure sur cette densité à 99% de
niveau de confiance en fonction de
kpc et les lignes
horizontales correspondent à des niveaux de confiance de 63% et 99%. La partie
droite de cette figure donne la limite supérieure sur cette densité à 99% de
niveau de confiance en fonction de 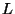 . Bien-sûr, celle-ci est une fonction
décroissante: plus important est le nombre de trous noirs "prisonniers" dans le
halo diffusif, plus contraignante est la limite. Entre
. Bien-sûr, celle-ci est une fonction
décroissante: plus important est le nombre de trous noirs "prisonniers" dans le
halo diffusif, plus contraignante est la limite. Entre 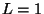 et
et 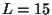 kpc
(valeurs extrêmes), les limites à 99% varient de
kpc
(valeurs extrêmes), les limites à 99% varient de
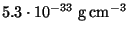 à
à
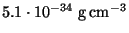 . En terme de densité numérique,
cela se traduit par
. En terme de densité numérique,
cela se traduit par
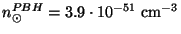 pour
pour 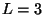 kpc. Il est important de donner les résultats sous l'une de
ces deux formes et non pas comme un taux d'explosion, comme cela est souvent fait,
car cette dernière variable n'a pas de réel sens physique: le nombre alors
dérivé est totalement dépendant du seuil arbitraire de l'expérience
considérée. La limite supérieure ici obtenue peut être traduite d'un point
de vue cosmologique (pour la densité en unité de densité critique)
en
kpc. Il est important de donner les résultats sous l'une de
ces deux formes et non pas comme un taux d'explosion, comme cela est souvent fait,
car cette dernière variable n'a pas de réel sens physique: le nombre alors
dérivé est totalement dépendant du seuil arbitraire de l'expérience
considérée. La limite supérieure ici obtenue peut être traduite d'un point
de vue cosmologique (pour la densité en unité de densité critique)
en
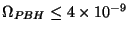 .
.
Cette valeur très faible permet de contraindre fortement les processus
susceptibles de créer des trous noirs et, en particulier, l'amplitude
des fluctuations aux petites échelles dans l'Univers primordial. Ce point sera
développé dans le chapitre suivant.




suivant: Gammas primaires
monter: Comment traquer les trous
précédent: Rayons cosmiques galactiques : processus
Table des matières
Aurelien Barrau
2004-07-01
![]() :
:
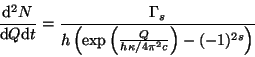
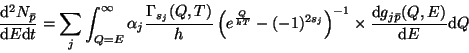
![]() d'antiprotons emis avec une énergie cinétique comprise entre
d'antiprotons emis avec une énergie cinétique comprise entre
![]() et
et ![]() par unité de volume et de temps doit être évalué. Il est
proportionnel au nombre
par unité de volume et de temps doit être évalué. Il est
proportionnel au nombre ![]() de PBH par unité de masse et de volume et au flux
individuel
de PBH par unité de masse et de volume et au flux
individuel
![]() émis par un PBH, soit
émis par un PBH, soit
![]() contribuent peu
compte-tenu de ce que leur température est très faible. Les trous noirs de
masse très petite contribuent également de façon sous-dominante, en
dépit de leur température élevée, à cause de leur faible densité
numérique (effet
contribuent peu
compte-tenu de ce que leur température est très faible. Les trous noirs de
masse très petite contribuent également de façon sous-dominante, en
dépit de leur température élevée, à cause de leur faible densité
numérique (effet ![]() dans le spectre de masse qui traduit physiquement
l'accélération de l'évaporation). C'est donc en fait la gamme de masse
dans le spectre de masse qui traduit physiquement
l'accélération de l'évaporation). C'est donc en fait la gamme de masse
![]() g -
g - ![]() g qui est essentiellement sondée à l'aide des
antiprotons cosmiques. La partie droite de cette figure présente l'effet d'une
coupure dans le spectre de masse initial due à la taille finie du rayon de Hubble
à la fin de l'inflation. Seuls les trous noirs formés à l'issue de cette
phase étant effectivement à prendre en compte (compte-tenu de la dilution
exponentielle de ceux formés avant celle-ci), une éventuelle masse de l'horizon
trop grande peut conduire à une réduction drastique de la population de PBH.
Avec la masse de Hubble à un instant
g qui est essentiellement sondée à l'aide des
antiprotons cosmiques. La partie droite de cette figure présente l'effet d'une
coupure dans le spectre de masse initial due à la taille finie du rayon de Hubble
à la fin de l'inflation. Seuls les trous noirs formés à l'issue de cette
phase étant effectivement à prendre en compte (compte-tenu de la dilution
exponentielle de ceux formés avant celle-ci), une éventuelle masse de l'horizon
trop grande peut conduire à une réduction drastique de la population de PBH.
Avec la masse de Hubble à un instant ![]() donnée
donnée
![]() s'écrit (en état stationnaire) :
s'écrit (en état stationnaire) :
![]() de
Dirac s'applique aux processus ayant lieu dans le disque galactique supposé
mince.
de
Dirac s'applique aux processus ayant lieu dans le disque galactique supposé
mince.
![]() (
(![]() est le
est le ![]() eme zéro de
eme zéro de
![]() et
et
![]() ).
La solution de l'équation (1.19) peut alors s'écrire
).
La solution de l'équation (1.19) peut alors s'écrire
![]() où les flux sont mesurés, la densité s'écrit
où les flux sont mesurés, la densité s'écrit
![]() interagissent avec la matière interstellaire et par des gains d'énergie quand
des processus de réaccélération prennent naissance. Ces variations sont
décrites par l'équation intégro-différentielle:
interagissent avec la matière interstellaire et par des gains d'énergie quand
des processus de réaccélération prennent naissance. Ces variations sont
décrites par l'équation intégro-différentielle:
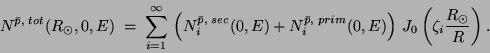
![]() alors que les primaires, dont les sources ne sont pas uniquement dans le disque
galactique mais aussi dans le halo, dependent directement de
alors que les primaires, dont les sources ne sont pas uniquement dans le disque
galactique mais aussi dans le halo, dependent directement de ![]() . Ce paramètre
n'étant pas contraint par l'étude exhaustive des noyaux jusqu'à Z=30
[31], il s'ensuit une dégénérescence sur les spectres primaires.
. Ce paramètre
n'étant pas contraint par l'étude exhaustive des noyaux jusqu'à Z=30
[31], il s'ensuit une dégénérescence sur les spectres primaires.
![]() généralisé qui tient compte des incertitudes
expérimentales disymétriques:
généralisé qui tient compte des incertitudes
expérimentales disymétriques:
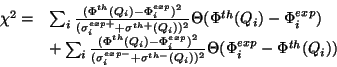
![]() et
et ![]() (
(![]() et
et ![]() ) sont les
erreurs théoriques et expérimentales positives (négatives). Une limite
supérieure sur la densité de PBH est calculée pour chaque valeur de taille
du halo diffusif (
) sont les
erreurs théoriques et expérimentales positives (négatives). Une limite
supérieure sur la densité de PBH est calculée pour chaque valeur de taille
du halo diffusif (![]() ). Les incertitudes théoriques tiennent compte à la fois
des aspects astrophysiques et nucléaires (
). Les incertitudes théoriques tiennent compte à la fois
des aspects astrophysiques et nucléaires (
![]() et
et
![]() ). La figure 1.9 présente, à gauche,
l'évolution du
). La figure 1.9 présente, à gauche,
l'évolution du ![]() en fonction de la densité pour
en fonction de la densité pour ![]() kpc et les lignes
horizontales correspondent à des niveaux de confiance de 63% et 99%. La partie
droite de cette figure donne la limite supérieure sur cette densité à 99% de
niveau de confiance en fonction de
kpc et les lignes
horizontales correspondent à des niveaux de confiance de 63% et 99%. La partie
droite de cette figure donne la limite supérieure sur cette densité à 99% de
niveau de confiance en fonction de ![]() . Bien-sûr, celle-ci est une fonction
décroissante: plus important est le nombre de trous noirs "prisonniers" dans le
halo diffusif, plus contraignante est la limite. Entre
. Bien-sûr, celle-ci est une fonction
décroissante: plus important est le nombre de trous noirs "prisonniers" dans le
halo diffusif, plus contraignante est la limite. Entre ![]() et
et ![]() kpc
(valeurs extrêmes), les limites à 99% varient de
kpc
(valeurs extrêmes), les limites à 99% varient de
![]() à
à
![]() . En terme de densité numérique,
cela se traduit par
. En terme de densité numérique,
cela se traduit par
![]() pour
pour ![]() kpc. Il est important de donner les résultats sous l'une de
ces deux formes et non pas comme un taux d'explosion, comme cela est souvent fait,
car cette dernière variable n'a pas de réel sens physique: le nombre alors
dérivé est totalement dépendant du seuil arbitraire de l'expérience
considérée. La limite supérieure ici obtenue peut être traduite d'un point
de vue cosmologique (pour la densité en unité de densité critique)
en
kpc. Il est important de donner les résultats sous l'une de
ces deux formes et non pas comme un taux d'explosion, comme cela est souvent fait,
car cette dernière variable n'a pas de réel sens physique: le nombre alors
dérivé est totalement dépendant du seuil arbitraire de l'expérience
considérée. La limite supérieure ici obtenue peut être traduite d'un point
de vue cosmologique (pour la densité en unité de densité critique)
en
![]() .
.