



suivant: Effet Unruh - Troisième
monter: Les trous noirs s'évaporent
précédent: Enoncé des quatre principes
Table des matières
Les effets quantiques violent la condition d'applicabilité du théorème de
l'aire de Hawking. En effet, l'évaporation quantique diminue l'aire des trous
noirs, et l'inégalité (1.9) n'est plus respectée. D'autre part, la
radiation des trous noirs est de nature thermique, et cette évaporation est
accompagnée d'une élévation de l'entropie dans l'espace environnant. On
doit donc construire l'entropie généralisée 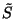 ,
définie par la somme de l'entropie du trou noir
,
définie par la somme de l'entropie du trou noir 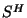 , de l'entropie de la
radiation et de la matière environnante
, de l'entropie de la
radiation et de la matière environnante 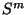 (
(
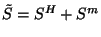 ), telle
qu'elle ne diminue
pas. En fait, on peut montrer que le taux d'augmentation (mesuré par
un observateur distant) de la masse et de l'entropie de la matière à
l'extérieur du trou noir s'écrit sous la forme :
), telle
qu'elle ne diminue
pas. En fait, on peut montrer que le taux d'augmentation (mesuré par
un observateur distant) de la masse et de l'entropie de la matière à
l'extérieur du trou noir s'écrit sous la forme :
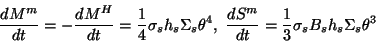 |
(1.10) |
où 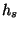 est le nombre d'état de polarisation du champ;
est le nombre d'état de polarisation du champ;
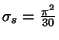 pour les bosons et
pour les bosons et
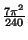 pour les fermions,
pour les fermions,
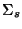 est la section efficace effective du trou noir,
est la section efficace effective du trou noir, 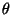 est sa
température et
est sa
température et 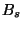 est un coefficient sans dimension de l'ordre de
l'unité.
D'autre part, la variation d'entropie
est un coefficient sans dimension de l'ordre de
l'unité.
D'autre part, la variation d'entropie 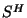 d'un trou noir sans rotation est
liée à la variation de sa masse par :
d'un trou noir sans rotation est
liée à la variation de sa masse par :
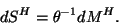 |
(1.11) |
Par comparaison entre (1.10) et (1.11), on trouve :
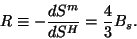 |
(1.12) |
Les calculs numériques ont démontré (autant qu'un calcul numérique puisse
démontrer, ce qui déplairait fortement à Wittgenstein...) que le coefficient 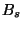 était
toujours plus grand que
était
toujours plus grand que 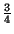 et ainsi que l'entropie généralisée
et ainsi que l'entropie généralisée
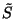 augmentait lors de l'émission radiative d'un trou noir. On peut
montrer que s'il existe une radiation de corps noir à une température
augmentait lors de l'émission radiative d'un trou noir. On peut
montrer que s'il existe une radiation de corps noir à une température
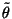 à l'extérieur du trou noir, l'entropie généralisée
augmente encore, sauf si
à l'extérieur du trou noir, l'entropie généralisée
augmente encore, sauf si
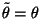 . Dans ce cas
particulier, l'augmentation de l'entropie due à l'évaporation est exactement
compensée par la diminution de celle due à
l'accrétion d'une radiation thermique autour du trou noir.
. Dans ce cas
particulier, l'augmentation de l'entropie due à l'évaporation est exactement
compensée par la diminution de celle due à
l'accrétion d'une radiation thermique autour du trou noir.
Ces arguments sont une base solide pour proposer le
Second principe généralisé :
Dans tout processus physique concernant un trou noir, l'entropie
généralisée 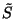 ne diminue pas :
ne diminue pas :
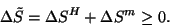 |
(1.13) |
Le fait que le second principe généralisé fournisse un lien entre des quantités très différentes, 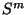 (qui
caractérise le "degré de chaos" dans la structure de la matière physique)
et
(qui
caractérise le "degré de chaos" dans la structure de la matière physique)
et 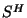 (qui est une caractéristique géométrique du trou noir), est une
nouvelle indication de leur profonde similitude. En fait, l'éventualité
très probable d'une telle relation prend sa source dans les équations
d'Einstein qui relient les caractéristiques physiques de la matière avec les
propriétés géométriques de l'espace-temps.
(qui est une caractéristique géométrique du trou noir), est une
nouvelle indication de leur profonde similitude. En fait, l'éventualité
très probable d'une telle relation prend sa source dans les équations
d'Einstein qui relient les caractéristiques physiques de la matière avec les
propriétés géométriques de l'espace-temps.




suivant: Effet Unruh - Troisième
monter: Les trous noirs s'évaporent
précédent: Enoncé des quatre principes
Table des matières
Aurelien Barrau
2004-07-01
![]() ,
définie par la somme de l'entropie du trou noir
,
définie par la somme de l'entropie du trou noir ![]() , de l'entropie de la
radiation et de la matière environnante
, de l'entropie de la
radiation et de la matière environnante ![]() (
(
![]() ), telle
qu'elle ne diminue
pas. En fait, on peut montrer que le taux d'augmentation (mesuré par
un observateur distant) de la masse et de l'entropie de la matière à
l'extérieur du trou noir s'écrit sous la forme :
), telle
qu'elle ne diminue
pas. En fait, on peut montrer que le taux d'augmentation (mesuré par
un observateur distant) de la masse et de l'entropie de la matière à
l'extérieur du trou noir s'écrit sous la forme :
![]() ne diminue pas :
ne diminue pas :