



suivant: Enoncé des quatre principes
monter: Les trous noirs s'évaporent
précédent: Effets quantiques - approche
Table des matières
La découverte (théorique pour le moment) de la radiation thermique des trous noirs a été
une véritable surprise pour les principaux spécialistes, même si de
nombreuses indications sur une relation entre la thermodynamique et la
physique des trous noirs avaient émergé avant cette découverte.
Wheeler semble avoir été le premier à remarquer la contradiction entre
l'existence des trous noirs dans la théorie classique de la gravitation et le
principe de non décroissance de l'entropie. En effet, si un trou noir
absorbe un corps chaud possédant une certaine entropie, un observateur
extérieur constate une diminution de l'entropie totale du monde accessible à
ses observations. Cette disparition peut être contournée formellement
si l'on attribue au trou noir une entropie égale à celle du corps absorbé.
En fait cette "solution" n'est manifestement pas satisfaisante puisque
classiquement, dès l'absorption, le
trou noir redevient stationnaire et perd complètement toute information
(dont l'entropie) sur le corps disparu.
Si l'on veut éviter de renoncer à ce principe fondamental de la
thermodynamique,
on doit postuler qu'un trou noir possède par lui-même
une certaine entropie et qu'un corps chaud plongeant dans celui-ci ne lui
transfère pas seulement sa masse, sa charge et son moment angulaire, mais
également sa propre entropie 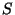 , augmentant ainsi celle du trou noir d'au
moins une telle quantité. Bekenstein remarqua que les propriétés de
l'une des caractéristiques
des trous noirs - l'aire
, augmentant ainsi celle du trou noir d'au
moins une telle quantité. Bekenstein remarqua que les propriétés de
l'une des caractéristiques
des trous noirs - l'aire 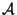 - étaient très semblables
à celles de l'entropie
puisque, d'après le théorème de Hawking, elle ne peut
diminuer dans aucun processus classique.
Ainsi, un trou noir arbitraire, à l'instar d'un système thermodynamique,
atteint-il un
équilibre (stationnaire) une fois les processus de relaxation
achevés. Dans cet état, il est entièrement décrit par un nombre
limité de paramètres :
- étaient très semblables
à celles de l'entropie
puisque, d'après le théorème de Hawking, elle ne peut
diminuer dans aucun processus classique.
Ainsi, un trou noir arbitraire, à l'instar d'un système thermodynamique,
atteint-il un
équilibre (stationnaire) une fois les processus de relaxation
achevés. Dans cet état, il est entièrement décrit par un nombre
limité de paramètres : 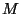 , la masse,
, la masse, 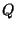 , la charge et
, la charge et 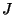 , le moment
angulaire; l'aire
, le moment
angulaire; l'aire 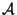 étant fonction des
ces trois variables :
étant fonction des
ces trois variables :
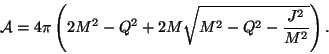 |
(1.4) |
Par inversion de la relation précédente1.1, on obtient la valeur de
l'énergie interne :
![\begin{displaymath}
M \equiv M(\mathcal{A}, J, Q) =
{\left[\frac{\pi\left[{\left...
...}\right)}^2 +
4J^2\right]}{\mathcal{A}}\right]}^{\frac{1}{2}}.
\end{displaymath}](img91.png) |
(1.5) |
Les énergies internes de deux trous noirs stationnaires présentant des entropies,
des moments angulaires et des charges électriques diffèrant respectivement
de 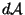 ,
, 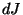 et
et 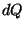 , se distinguent de :
, se distinguent de :
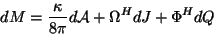 |
(1.6) |
où
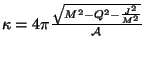 est la
gravité de surface;
est la
gravité de surface;
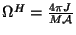 est la
vélocité angulaire, et
est la
vélocité angulaire, et
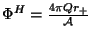 est le
potentiel électrique du trou noir (
est le
potentiel électrique du trou noir (
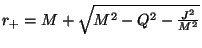 correspondant à l'horizon causal en géométrie de Kerr-Newmann, i.e
dans le cas d'un trou noir chargé et en rotation). Le second et le troisième terme
décrivent respectivement les changements d'énergie de rotation et d'énergie
électrique.
correspondant à l'horizon causal en géométrie de Kerr-Newmann, i.e
dans le cas d'un trou noir chargé et en rotation). Le second et le troisième terme
décrivent respectivement les changements d'énergie de rotation et d'énergie
électrique.
Cette relation est similaire au premier principe de la thermodynamique.
L'analogue de la température (la variable conjuguée de l'entropie) est une
quantité proportionnelle à la gravité de surface 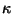 . Le résultat
de Hawking sur la nature thermique de la radiation d'un trou noir stationnaire
n'amène pas seulement à cette analogie mais fixe aussi le coefficient
reliant la température
. Le résultat
de Hawking sur la nature thermique de la radiation d'un trou noir stationnaire
n'amène pas seulement à cette analogie mais fixe aussi le coefficient
reliant la température 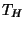 au champ à l'horizon
au champ à l'horizon 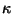 .
On peut remarquer que la relation (1.6) est identique au premier principe de
la thermodynamique,
.
On peut remarquer que la relation (1.6) est identique au premier principe de
la thermodynamique,
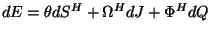 ,
si l'on suppose l'expression suivante pour l'entropie du trou noir :
,
si l'on suppose l'expression suivante pour l'entropie du trou noir :
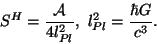 |
(1.7) |
Cette quantité est connue sous le nom d'entropie de Bekenstein-Hawking.




suivant: Enoncé des quatre principes
monter: Les trous noirs s'évaporent
précédent: Effets quantiques - approche
Table des matières
Aurelien Barrau
2004-07-01
![]() , augmentant ainsi celle du trou noir d'au
moins une telle quantité. Bekenstein remarqua que les propriétés de
l'une des caractéristiques
des trous noirs - l'aire
, augmentant ainsi celle du trou noir d'au
moins une telle quantité. Bekenstein remarqua que les propriétés de
l'une des caractéristiques
des trous noirs - l'aire ![]() - étaient très semblables
à celles de l'entropie
puisque, d'après le théorème de Hawking, elle ne peut
diminuer dans aucun processus classique.
Ainsi, un trou noir arbitraire, à l'instar d'un système thermodynamique,
atteint-il un
équilibre (stationnaire) une fois les processus de relaxation
achevés. Dans cet état, il est entièrement décrit par un nombre
limité de paramètres :
- étaient très semblables
à celles de l'entropie
puisque, d'après le théorème de Hawking, elle ne peut
diminuer dans aucun processus classique.
Ainsi, un trou noir arbitraire, à l'instar d'un système thermodynamique,
atteint-il un
équilibre (stationnaire) une fois les processus de relaxation
achevés. Dans cet état, il est entièrement décrit par un nombre
limité de paramètres : ![]() , la masse,
, la masse, ![]() , la charge et
, la charge et ![]() , le moment
angulaire; l'aire
, le moment
angulaire; l'aire ![]() étant fonction des
ces trois variables :
étant fonction des
ces trois variables :
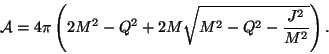
![\begin{displaymath}
M \equiv M(\mathcal{A}, J, Q) =
{\left[\frac{\pi\left[{\left...
...}\right)}^2 +
4J^2\right]}{\mathcal{A}}\right]}^{\frac{1}{2}}.
\end{displaymath}](img91.png)
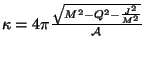 est la
gravité de surface;
est la
gravité de surface;
![]() . Le résultat
de Hawking sur la nature thermique de la radiation d'un trou noir stationnaire
n'amène pas seulement à cette analogie mais fixe aussi le coefficient
reliant la température
. Le résultat
de Hawking sur la nature thermique de la radiation d'un trou noir stationnaire
n'amène pas seulement à cette analogie mais fixe aussi le coefficient
reliant la température ![]() au champ à l'horizon
au champ à l'horizon ![]() .
On peut remarquer que la relation (1.6) est identique au premier principe de
la thermodynamique,
.
On peut remarquer que la relation (1.6) est identique au premier principe de
la thermodynamique,
![]() ,
si l'on suppose l'expression suivante pour l'entropie du trou noir :
,
si l'on suppose l'expression suivante pour l'entropie du trou noir :