Effets quantiques - approche intuitive

Les effets quantiques sont inexistants pour les trous noirs massifs (i.e. typiquement au-delà de quelques $10^{-18}M_{\odot}$ où $M_{\odot}$ représente la masse du Soleil) mais peuvent se manifester au voisinage des objets les plus compacts. Ceci n'est pas surprenant puisque la gravité de surface d'un trou noir (et la force de marée) est d'autant plus forte que celui-ci est petit. On peut fixer les idées en théorie newtonienne : la masse apparaît linéairement au numérateur de la force gravitationnelle, favorisant effectivement les larges trous noirs, mais le rayon de Schwarzschild (lui-même proportionnel à la masse) apparaît au dénominateur de cette même force de façon quadratique. Les trous noirs légers sont donc les plus propices à l'existence d'un champ intense à l'extérieur de l'horizon. Ce sont aussi les plus denses : la masse volumique d'un trou noir supermassif ne dépasse pas celle de l'eau...

Considérons ici une approche intuitive pour laquelle le champ gravitationnel d'un trou noir est classique et fixé (i.e. sans backreaction). Dans le vide, des particules virtuelles sont constamment créées, interagissent entre elles et s'annihilent. En présence d'un champ extérieur, certaines d'entre elles peuvent acquérir suffisamment d'énergie et devenir réelles.

Soit $w$ la probabilité de créer une particule dans un champ extérieur $\Gamma$ (pas nécessairement gravitationnel). Pour des corpuscules virtuels d'une même paire, la probabilité que l'un se trouve à la distance $l$ de l'autre est proportionnelle à $exp(-\frac{l}{\lambda_m})$, où $\lambda_m=\frac{\hbar}{mc}$ est la longueur d'onde Compton de l'objet de masse $m$. Si le travail du champ extérieur sur cette distance $l$ (égal à $\Gamma g l$ si l'on note $g$ la charge de la particule) est supérieur à l'énergie de masse des particules ($2mc^2$), alors les particules peuvent devenir réelles. La probabilité associée est donc $w= A exp(-\frac{\beta m^2 c^3}{\hbar g \Gamma})$ où $A$ et $\beta$ dépendent des caractéristiques du champ.

Un exemple connu de création de particules dans un champ extérieur est celui des paires électrons-positons en présence d'un champ électrique. Schwinger a montré [7] que le taux de production par unité de temps et de volume s'écrit :

$$\frac{d^2N}{dtdV}=\frac{e^2E^2}{\pi^2\hbar ^2c}\sum_{n=1}^{\infty}\frac{1}{n^2}\exp\left(-\frac{\pi m^2c^3n}{eE\hbar}\right).$$

Si l'on applique naïvement cette relation à un champ gravitationnel $\Gamma$, où le rôle de la charge $e$ est joué par la masse $m$, on obtient :

$$w=A \exp\left( -\frac{mc^2}{\theta}\right)\mbox{, avec } \theta=\frac{\hbar \Gamma}{\beta \pi c}.$$ (1.1)

En d'autres termes, la probabilité de créer des particules de masse $m$ présente un comportement Boltzmannien avec une température effective (en unité d'énergie) $\theta$.

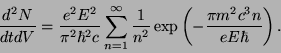
Dans le cas des trous noirs, Stephen Hawking [8] a montré que le vide présentait des instabilités et en a déduit l'existence d'une température effective $T_H=\hbar \kappa/(2\pi c k)$ où $\kappa$ est la gravité de surface caractérisant la "force" du champ gravitationnel sur l'horizon.

Pour un trou noir de Schwarzschild, $\kappa = \frac{c^4}{4GM}$, et l'expression de la température de Hawking est :

$$T_H=\frac{\hbar c^3}{8 \pi GkM}.$$ (1.2)

Il s'agit sans doute d'une des plus belles équations de la physique contenant toutes les constantes fondamentales. La probabilité de création d'une particule d'énergie $E$ mesurée à l'infini est alors donnée par :

$$w \sim \exp \left(-\frac{E}{kT_H}\right).$$ (1.3)

Si on se réfère à l'équation (1.1), ce résultat est cohérent en considérant que la force du champ $\Gamma$ coïncide avec la gravité de surface du trou noir (pour $\beta =2$). Le processus de Hawking, bien que similaire aux effets de la création de particules dans un champ électrique, présente néanmoins une différence fondamentale : puisque les états d'énergie négative sont situés à l'intérieur du trou noir, seule une des particules créées peut apparaître à l'extérieur et atteindre un observateur distant. Celui-ci n'aura alors accès qu'à une partie du système quantique total.