Nous proposons ici une nouvelle approche pour sonder expérimentalement un
comportement gravitationnel quantique auprès des collisionneurs.
La littérature autour des modèles supposant l'existence de dimensions
supplémentaires est extrêmement riche (voir, par exemple, [91] pour
une revue récente).
Entre autres intérêts, ces scenarios permettent de résoudre le problème de la hiérarchie
entre les échelles électro-faible et gravitationnelle. Dans le cas des large extra dimensions [92], l'approche est purement géométrique
avec une gravité qui se propage seule dans le bulk. Le théorème de
Gauss permet alors de lier simplement l'échelle de Planck de la théorie
effective quadridimentionnelle ![]() à l'échelle de Planck fondamentale
D-dimentionnelle
à l'échelle de Planck fondamentale
D-dimentionnelle ![]() :
:
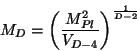
Une autre manière prometteuse d'obtenir une échelle de Planck dans le
domaine du TeV apparaît dans les modèles utilisant des warped
extra-dimensions, tels que dans les scenarios de type Randall-Sundrum [93].
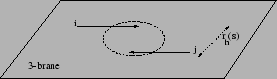
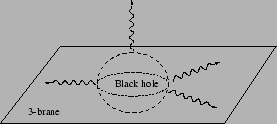
Sans entrer dans les multiples détails de ces modèles, le point fondamental pour nous dans le cadre de cette étude est qu'ils conduisent génériquement à la formation de trous noirs auprès des collisionneurs [94,95] : lorsque l'énergie dans le centre de masse, pour des partons dont le paramètre d'impact est inférieur au rayon gravitationnel, est plus grande que l'échelle de Planck, une surface close doit se former (voir figure 3.1 pour une représentation intuitive). Cette idée a suscité un intérêt considérable ces dernières années [96].
|
Les premières études ont montré que le LHC pourrait devenir une
véritable usine à trous noirs. La mauvaise nouvelle pour le physicien des
particules (i.e. la formation d'un horizon qui masque toute la
microphysique) se trouverait alors balancée par une excellente nouvelle pour
le physicien "tout court" : il serait possible de reconstruire, à partir de
l'évaporation de ces trous noirs, la
dimensionalité de l'espace temps et d'accéder alors à la structure
fondamentale de notre géométrie [94].
Une des faiblesses de ces approches est d'utiliser systématiquement les
métriques de Schwarzschild ou de Kerr (généralisées à D dimensions) pour
traiter le comportement des trous noirs. Une telle approche est
nécessairement lacunaire : d'une part ces métriques intrinsèquement instables
(à ![]() ),
d'autre part la relativité générale n'est certainement pas la bonne
théorie dans la région de Planck. Nous avons donc proposé d'étudier les
trous noirs de Gauss-Bonnet afin de montrer que, si des trous noirs sont formés au LHC, il
pourra être possible d'aller bien au-delà de la mesure de la dimentionalité de l'espace
temps. Ce terme quadratique en courbure (déjà
introduit dans le chapitre 2.2 de ce mémoire) est très important parce qu'il
constitue sans doute un premier pas vers une théorie quantique de la
gravitation. Comme montré dans [97], il est la contribution dominante
au NLO (ordre au-delà du dominant) et, si l'on requiert une absence de fantômes (termes de masses
négatifs) dans les développement en courbure, le terme correspondant doit être celui de Gauss-Bonnet :
),
d'autre part la relativité générale n'est certainement pas la bonne
théorie dans la région de Planck. Nous avons donc proposé d'étudier les
trous noirs de Gauss-Bonnet afin de montrer que, si des trous noirs sont formés au LHC, il
pourra être possible d'aller bien au-delà de la mesure de la dimentionalité de l'espace
temps. Ce terme quadratique en courbure (déjà
introduit dans le chapitre 2.2 de ce mémoire) est très important parce qu'il
constitue sans doute un premier pas vers une théorie quantique de la
gravitation. Comme montré dans [97], il est la contribution dominante
au NLO (ordre au-delà du dominant) et, si l'on requiert une absence de fantômes (termes de masses
négatifs) dans les développement en courbure, le terme correspondant doit être celui de Gauss-Bonnet :
![]() . De plus, comme nous l'avons rappelé
au chapitre précédent, ce terme apparaît naturellement dans les
théories de cordes hétérotiques [98], permet la localisation du mode zéro du
graviton sur le brane [99] et il a été utilisé avec succès en cosmologie (en
particulier pour le problème de la constante cosmologique) [100] et en physique des
trous noirs (en particulier pour le problème de la fin de vie) [101]. Nous utilisons
donc ici une telle action :
. De plus, comme nous l'avons rappelé
au chapitre précédent, ce terme apparaît naturellement dans les
théories de cordes hétérotiques [98], permet la localisation du mode zéro du
graviton sur le brane [99] et il a été utilisé avec succès en cosmologie (en
particulier pour le problème de la constante cosmologique) [100] et en physique des
trous noirs (en particulier pour le problème de la fin de vie) [101]. Nous utilisons
donc ici une telle action :
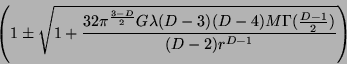
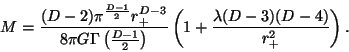
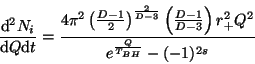
![\begin{displaymath}\frac{{\rm d}M}{{\rm d}r_+}
= \frac{(D-2)\pi^{\frac{D-1}{2}}r...
...frac{D-1}{2} )}\left[ (D-3)r_+^2+(D-5)(D-4)(D-3)\lambda \right]\end{displaymath}](img580.png)
![\begin{displaymath}\frac{{\rm d}M}{{\rm d}t}=-\frac{4\pi ^6}{15}
\left( \frac{D-...
...-1}{D-3} \right)
r_+^2 T_{BH}^4\left[\frac{7}{8}N_f+N_b\right],\end{displaymath}](img581.png)
![\begin{displaymath}N_{tot}
= \frac{15(D-2)\pi^{\frac{D-9}{2}}\zeta(3)}{\Gamma(\f...
...c{r_{init +}^{D-2}}{D-2}+
2(D-3)\lambda r_{init +}^{D-4}\right]\end{displaymath}](img584.png)
|
Afin d'étudier la capacité du LHC à mesurer la constante de couplage (de Gauss-Bonnet,
i.e. de corde) ![]() , nous avons fixé l'échelle de Planck à 1 TeV. Le nombre de
trous noirs formés par bin de masse est alors calculé par une convolution avec les fonctions
de luminosité partoniques et ré-évalué en tenant compte de la diminution du rayon
gravitationnel due au terme de Gauss-Bonnet. Connaissant ainsi la section efficace, nous avons
mis en place en simulation Monte-Carlo qui génère, pour chaque événement de type trou
noir, les particules selon le spectre de Hawking modifié avec une pondération liée au
nombre de degrés de liberté internes. Etant donné que l'évaporation a lieu
essentiellement en ondes
, nous avons fixé l'échelle de Planck à 1 TeV. Le nombre de
trous noirs formés par bin de masse est alors calculé par une convolution avec les fonctions
de luminosité partoniques et ré-évalué en tenant compte de la diminution du rayon
gravitationnel due au terme de Gauss-Bonnet. Connaissant ainsi la section efficace, nous avons
mis en place en simulation Monte-Carlo qui génère, pour chaque événement de type trou
noir, les particules selon le spectre de Hawking modifié avec une pondération liée au
nombre de degrés de liberté internes. Etant donné que l'évaporation a lieu
essentiellement en ondes ![]() , il y a peu de modes dans le bulk et on peu se restreindre au
brane. La fragmentation modifiant considérablement le spectre des quarks
et gluons, l'analyse se restreint aux électrons et photons de haute énergie. Nous avons
également vérifié avec Pythia [102] que seule une faible fraction des leptons
et modes électromagnétiques émis tombaient dans des jets hadroniques. Enfin, le bruit
irréductible du modèle standard Z(ee)+jets et
, il y a peu de modes dans le bulk et on peu se restreindre au
brane. La fragmentation modifiant considérablement le spectre des quarks
et gluons, l'analyse se restreint aux électrons et photons de haute énergie. Nous avons
également vérifié avec Pythia [102] que seule une faible fraction des leptons
et modes électromagnétiques émis tombaient dans des jets hadroniques. Enfin, le bruit
irréductible du modèle standard Z(ee)+jets et ![]() +jets reste négligeable. La
résolution en énergie
du détecteur est paramétrisée par [103]
+jets reste négligeable. La
résolution en énergie
du détecteur est paramétrisée par [103]
![]() avec
avec
![]() %
%
![]() et
et ![]() %. L'évolution temporelle du trou
noir est également totalement prise en compte. Une fois que toutes les particules ont
été émises, l'analyse détaillée est appliquée pour chaque bin de masse. Nous en
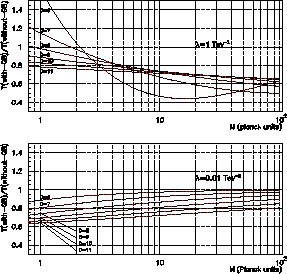
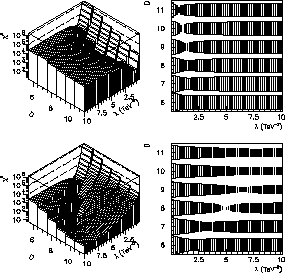
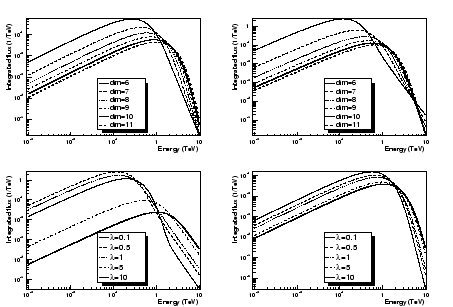
déduisons (cf [87] pour un tableau explicite des incertitudes exactes), comme le montre
la figure 3.3, qu'il est effectivement possible de reconstruire correctement le nombre
de dimensions supplémentaires et la constante de couplage
%. L'évolution temporelle du trou
noir est également totalement prise en compte. Une fois que toutes les particules ont
été émises, l'analyse détaillée est appliquée pour chaque bin de masse. Nous en
déduisons (cf [87] pour un tableau explicite des incertitudes exactes), comme le montre
la figure 3.3, qu'il est effectivement possible de reconstruire correctement le nombre
de dimensions supplémentaires et la constante de couplage ![]() au LHC. Cela signifie que le LHC
permettrait non seulement (dans le cadre de ces modèles à dimensions supplémentaires
associées à de grands volumes) d'accéder à la structure ultime de l'espace-temps, mais
aussi de donner une information précieuse sur la voie à suivre pour généraliser la
gravité d'Einstein dans la région de Planck. Il est à noter que le tagging d'un événement comme étant de type "trou noir" est très simple et non ambigu
[95] : la topologie et la grande abondance de degrés de libertés leptoniques
permettent une signature efficace.
au LHC. Cela signifie que le LHC
permettrait non seulement (dans le cadre de ces modèles à dimensions supplémentaires
associées à de grands volumes) d'accéder à la structure ultime de l'espace-temps, mais
aussi de donner une information précieuse sur la voie à suivre pour généraliser la
gravité d'Einstein dans la région de Planck. Il est à noter que le tagging d'un événement comme étant de type "trou noir" est très simple et non ambigu
[95] : la topologie et la grande abondance de degrés de libertés leptoniques
permettent une signature efficace.
|
Plusieurs voies pour de futures investigations s'ouvrent autour de cette perspective. D'abord,
en ce qui concerne la section efficace de production de trous noirs. Dans l'étude
précédente, nous avons simplement autorisé une possible suppression de la section efficace
pour tenir compte de la non-nullité du paramètre d'impact ![]() . En fait, le problème du calcul
explicite de la section efficace à
. En fait, le problème du calcul
explicite de la section efficace à ![]() et
et ![]() est très complexe [104,105].
L'existence de trous noirs (i.e. la formation de surfaces closes) est maintenant
établie mais
les valeurs exactes des probabilités ne sont pas connues. Il serait important d'aller plus
loin dans cette voie, soit en suivant une approche heuristique fondée sur la modification du
rayon gravitationnel due au moment angulaire associée à la valeur de
est très complexe [104,105].
L'existence de trous noirs (i.e. la formation de surfaces closes) est maintenant
établie mais
les valeurs exactes des probabilités ne sont pas connues. Il serait important d'aller plus
loin dans cette voie, soit en suivant une approche heuristique fondée sur la modification du
rayon gravitationnel due au moment angulaire associée à la valeur de ![]() , soit en suivant
une approche rigoureuse de calcul explicite de la géométrie du problème. Cette dernière
possibilité (à laquelle s'est intéressé Penrose) est hautement non triviale et
requiert de booster les champs de Schwarzshild générés par les particules avant de
rechercher des solutions "fermées".
, soit en suivant
une approche rigoureuse de calcul explicite de la géométrie du problème. Cette dernière
possibilité (à laquelle s'est intéressé Penrose) est hautement non triviale et
requiert de booster les champs de Schwarzshild générés par les particules avant de
rechercher des solutions "fermées".
A plus court terme, un point important consisterait à tenir compte de ce que les trous noirs
ici considérés sont nécessairement en rotation (i.e. de type Kerr) puisque ![]() n'est
jamais strictement nul. La thermodynamique des trous noirs de Kerr est connue. Nous sommes en
train d'étudier celle des trous noirs de Kerr-Gauss-Bonnet à D dimensions.
La conjugaison d'un moment
angulaire et de termes d'ordres supérieurs en courbure est sans doute une approche assez
réaliste du problème. Bien que qualitativement identiques, les résultats précédents
pourraient être quantitativement modifiés. La méthode générale de dérivation de la
métrique (puis de la température, ce point est simple) de Kerr-Gauss-Bonnet est assez
élémentaire (il suffit de suivre l'approche utilisée par [106] pour obtenir la
métrique de Kerr D-dimentionnelle). En revanche, les calculs sont très lourds car les
équations différentielles (de type Abel-II) qui apparaîssent n'ont pas de solutions
analytiques. Nous pensons qu'il serait intéressant de procéder à des développements
asymptotiques autour de l'horizon, ce travail est en cours.
n'est
jamais strictement nul. La thermodynamique des trous noirs de Kerr est connue. Nous sommes en
train d'étudier celle des trous noirs de Kerr-Gauss-Bonnet à D dimensions.
La conjugaison d'un moment
angulaire et de termes d'ordres supérieurs en courbure est sans doute une approche assez
réaliste du problème. Bien que qualitativement identiques, les résultats précédents
pourraient être quantitativement modifiés. La méthode générale de dérivation de la
métrique (puis de la température, ce point est simple) de Kerr-Gauss-Bonnet est assez
élémentaire (il suffit de suivre l'approche utilisée par [106] pour obtenir la
métrique de Kerr D-dimentionnelle). En revanche, les calculs sont très lourds car les
équations différentielles (de type Abel-II) qui apparaîssent n'ont pas de solutions
analytiques. Nous pensons qu'il serait intéressant de procéder à des développements
asymptotiques autour de l'horizon, ce travail est en cours.
Ensuite, il serait légitime d'ajouter une constante cosmologique dans l'action
gravitationnelle. D'un point de vue théorique, la motivation est grande, compte-tenu des
très nombreux développements actuels portant sur les correspondances dS et AdS (deSitter et
Anti-deSitter) / CFT (théorie de champ conforme). D'un point de vue expérimental, il est peu
probable à mon sens que l'effet d'un terme constant dans le lagrangien joue un rôle très
conséquent dans la région de Planck (i.e. des fortes courbures). Mais des transitions
singulières changeant la topologie de la solution ne sont pas à exclure. Suivant [107],
cette démarche ne serait pas trop complexe à mettre un ![]() uvre. Il serait assez cocasse
qu'une information fondamentale sur la constante cosmologique (attention, à D-dimensions, donc
sans lien direct avec le terme
uvre. Il serait assez cocasse
qu'une information fondamentale sur la constante cosmologique (attention, à D-dimensions, donc
sans lien direct avec le terme ![]() mesuré à 4 dimensions en cosmologie) vienne du
LHC !
mesuré à 4 dimensions en cosmologie) vienne du
LHC !
Enfin, il me semble qu'il pourrait être important de pousser plus avant les liens avec
l'inflation. Ceci dans deux directions : la première consisterait à étudier le lien entre
les modèles de type Gauss-Bonnet utilisés ici et les modèles où l'inflation est
générée par des termes quadratiques en courbure. Il n'est, en effet, pas nécessaire
d'avoir un champ scalaire dans le lagrangien pour qu'il y ait inflation : un effet de courbure
peut conduire au même résultat. Voir si les éventuelles contraintes du LHC sur ![]() sont en accord avec les modèles d'inflation me paraît essentiel à la complétude de la
démarche. La tâche n'est néanmoins pas simple car la dynamique du processus doit être
étudiée en détails, ce qui n'est pas une mince affaire. La seconde direction consisterait à
étudier la production transplanckienne thermique de trous noirs dans l'Univers primordial.
Après tout, si le LHC peut aller au-delà de l'échelle de Planck, pourquoi pas l'Univers
primordial ! Bien-sûr, ces aspects sont très spéculatifs, mais il serait intéressant de
voir, dans ce cadre, si une limite supérieure sur l'échelle d'énergie primordiale
peut être obtenue. Je pense que celle-ci viendra de la contrainte consistant à demander que
les trous noirs ainsi formés s'évaporent avant la nucléosynthèse. J'ignore si le travail
est délicat mais je ne le pense pas et il sera entrepris à court terme.
sont en accord avec les modèles d'inflation me paraît essentiel à la complétude de la
démarche. La tâche n'est néanmoins pas simple car la dynamique du processus doit être
étudiée en détails, ce qui n'est pas une mince affaire. La seconde direction consisterait à
étudier la production transplanckienne thermique de trous noirs dans l'Univers primordial.
Après tout, si le LHC peut aller au-delà de l'échelle de Planck, pourquoi pas l'Univers
primordial ! Bien-sûr, ces aspects sont très spéculatifs, mais il serait intéressant de
voir, dans ce cadre, si une limite supérieure sur l'échelle d'énergie primordiale
peut être obtenue. Je pense que celle-ci viendra de la contrainte consistant à demander que
les trous noirs ainsi formés s'évaporent avant la nucléosynthèse. J'ignore si le travail
est délicat mais je ne le pense pas et il sera entrepris à court terme.
Pour conclure sur cette partie, signalons également que des approches
totalement indépendantes
du modèle EDGB conduisent aussi à la prédiction de reliques stables [73]. Ces
modèles, fondés sur le groupe de renormalisation, demeurent valides à ![]() . Nous aimerions
évaluer l'effet de l'énergie manquante associée comme une autre direction d'investigation
possible au-delà de la dimensionalité de l'espace-temps. Ce point a été évoqué avec A.
Bonanno et pourrait faire l'objet d'une collaboration ultérieure, selon les résultats
préliminaires.
. Nous aimerions
évaluer l'effet de l'énergie manquante associée comme une autre direction d'investigation
possible au-delà de la dimensionalité de l'espace-temps. Ce point a été évoqué avec A.
Bonanno et pourrait faire l'objet d'une collaboration ultérieure, selon les résultats
préliminaires.
Bien-sûr, une prise en compte plus réaliste de détecteur, fondée sur une simulation complète serait très bienvenue. Une discussion est en cours avec l'équipe ATLAS du LPSC.