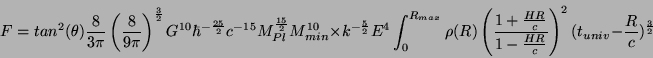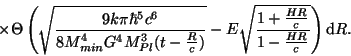suivant: Matière noire [79]
monter: Les trous noirs primordiaux
précédent: Univers primordial [45]
Table des matières
Ce paragraphe s'intéresse à la fin de vie des trous noirs primordiaux
et présente un modèle, spéculatif mais cohérent, pour rendre compte
du comportement lorsque la masse devient très petite.
L'évaporation de Hawking devient divergente lorsque la masse du trou noir
tend vers zéro. En effet, le spectre de masse s'écrivant
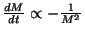 (comme montré dans le premier paragraphe de ce chapitre),
on voit bien que
(comme montré dans le premier paragraphe de ce chapitre),
on voit bien que
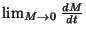 n'est pas définie. De plus, dans cette image, l'évaporation
complète conduirait sans doute à une singularité nue qui contredirait le
principe de censure cosmique de Penrose.
Le formalisme habituel ne peut plus s'appliquer lorsque la masse devient de
l'ordre de la masse de Planck. La description quasi-classique est inadaptée
et les phénomènes de gravité
quantique doivent être pris en compte.
n'est pas définie. De plus, dans cette image, l'évaporation
complète conduirait sans doute à une singularité nue qui contredirait le
principe de censure cosmique de Penrose.
Le formalisme habituel ne peut plus s'appliquer lorsque la masse devient de
l'ordre de la masse de Planck. La description quasi-classique est inadaptée
et les phénomènes de gravité
quantique doivent être pris en compte.
Étant donné que la Relativité Générale n'est pas une théorie
renormalisable, sa quantification directe est impossible. Pour construire une
théorie semi-classique de la gravitation, à titre de modèle provisoire,
le lagrangien standard doit être
généralisé. Une des approches possibles consiste à
étudier un développement de l'action en courbure
scalaire, c'est-à-dire à autoriser des corrections de courbure d'ordres
élevés. Cette démarche considère que dans le régime asymptotique, telle que se présente la gravitation
en cosmologie ou en astrophysique, seul le terme d'ordre le plus bas contribue
et la théorie d'Einstein est bien vérifiée. Mais lorsque l'on
considère des phénomènes qui prennent naissance au voisinage immédiat
d'un petit trou noir, i.e. dans une zone où la courbure de
l'espace-temps est très élevée, les termes d'ordres supérieurs doivent
intervenir.
Nous nous focalisons ici, d'un point de vue phénoménologique, sur
le terme de second ordre (il a été montré que les ordres supérieurs ne
changent, qualitativement, pas le résultat, cf. plus loin) appelé
``invariant de Gauss-Bonnet" :
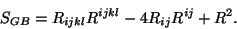
Il existe plusieurs façons de justifier la forme de ce terme [62].
On peut le voir comme une simple extension au second ordre à partir des
tenseurs de Riemann et de Ricci et du scalaire de Ricci dont les coefficients
sont dictés par la loi de Landau [63]. On peut aussi, plus spécifiquement, noter que ce terme
apparaît comme la correction quantique dominante dans l'action des théories de
cordes hétérotiques [64]. Il représente de plus, à cinq
dimensions, la seule combinaison invariante de termes conduisant à des
équations de champ du second ordre en tenseur métrique [65]
[66]. Il a même été montré, dans le cadre des approches
multi-dimensionnelles, que le mode-zéro du
graviton est localisé sur le brane quand ce terme est inclus dans
l'action du bulk [67]. Enfin, le terme de Gauss-Bonnet est
aujourd'hui très étudié en cosmologie [68], en particulier dans les modèles
Randall-Sundrun de type II (équivalents à une gravité
à quatre dimensions couplée à une théorie de champ conforme par la
correspondance AdS/CFT [69])
où un brane isotrope et homogène se
propage au sein d'un espace Schwarzschild-Anti-de Sitter à cinq dimensions
[93]. En résumé, il est l'une des extensions de la relativité d'Einstein les
plus prometteuses et se retrouve à partir de plusieurs approches indépendantes dont
certaines sont modèle indépendantes.
Partant donc de ce modèle (où le terme de Gauss-Bonnet est dynamiquement couplé
à un champ scalaire - considéré ici comme le champ de dilaton puisque le
couplage est imposé par les théories de cordes), nous nous intéressons à l'étude de la fin de vie des
trous noirs primordiaux. Nous montrons d'abord que la loi d'évaporation de
Hawking doit être fortement modifiée au voisinage de la masse de Planck. La
nouvelle forme du spectre émis est calculée à partir de l'approximation
WKB, en prenant la partie imaginaire de l'action (de façon analogue à
l'effet tunnel). Pour ce faire, nous nous plaçons dans les coordonnées de
Painlevé qui, à la différence de celles de Schwarzschild, évitent la
singularité de coordonnées en 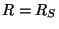 , et nous paramétrons les fonctions
``correctives" par rapport au comportement asymptotique de Schwarzschild. Le taux de perte de
masse présente, dans cette approche, une forme très caractéristique avec un
maximum nettement marqué puis une lente décélération correspondant à la
vie post-mortem du trou noir durant laquelle sa température augmente
mais l'énergie des quanta émis diminue [71]. Intuitivement, on peut comprendre ce
comportement en imaginant que la température correspond en fait à l'énergie
des particules qui se couplent le plus naturellement avec le trou noir (i.e. dont
la longueur d'onde Compton est de l'ordre du rayon gravitationnel). Elle ne peut donc
qu'augmenter au cours de l'évaporation. En revanche, l'énergie moyenne des quanta émis
commence à diminuer à partir du moment où la limite topologique qui impose une masse
minimale en dessous de laquelle le trou noir ne peut pas transiter [72] tronque
la distribution naturelle de probabilité. Tout se passe comme si le trou noir
``essayait"
d'émettre un quantum toute les
, et nous paramétrons les fonctions
``correctives" par rapport au comportement asymptotique de Schwarzschild. Le taux de perte de
masse présente, dans cette approche, une forme très caractéristique avec un
maximum nettement marqué puis une lente décélération correspondant à la
vie post-mortem du trou noir durant laquelle sa température augmente
mais l'énergie des quanta émis diminue [71]. Intuitivement, on peut comprendre ce
comportement en imaginant que la température correspond en fait à l'énergie
des particules qui se couplent le plus naturellement avec le trou noir (i.e. dont
la longueur d'onde Compton est de l'ordre du rayon gravitationnel). Elle ne peut donc
qu'augmenter au cours de l'évaporation. En revanche, l'énergie moyenne des quanta émis
commence à diminuer à partir du moment où la limite topologique qui impose une masse
minimale en dessous de laquelle le trou noir ne peut pas transiter [72] tronque
la distribution naturelle de probabilité. Tout se passe comme si le trou noir
``essayait"
d'émettre un quantum toute les 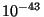 s (soit 10
s (soit 10 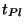 si l'on
considère, par exemple, que sa masse est
de l'ordre de 10
si l'on
considère, par exemple, que sa masse est
de l'ordre de 10 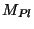 ) mais que l'immense majorité du spectre naturel lui était
quantiquement
interdit : seul dans le cas où l'évènement ``tombe" dans la petite portion pour laquelle
l'évaporation peut
avoir lieu (i.e. conduisant à une masse supérieure à la masse minimale), le quantum
est émis et la masse diminue, rendant la prochaine itération moins probable encore et
l'énergie moyenne plus faible.
) mais que l'immense majorité du spectre naturel lui était
quantiquement
interdit : seul dans le cas où l'évènement ``tombe" dans la petite portion pour laquelle
l'évaporation peut
avoir lieu (i.e. conduisant à une masse supérieure à la masse minimale), le quantum
est émis et la masse diminue, rendant la prochaine itération moins probable encore et
l'énergie moyenne plus faible.
Le flux intégré de ces reliques
est calculé au niveau de la Terre en supposant une distribution spatiale standard, en
tenant compte du décalage spectral et, surtout, de l'évolution des sources qui,
lorsqu'elles sont éloignées, sont vues dans un état plus précoce de leur
vie. Cette compétition entre des effet antagonistes (le décalage spectral
diminue l'énergie alors que la précocité favorise l'émission à haute
énergie) conduit à un spectre intégré de forme très particulière
dont l'éventuelle détectabilité est étudiée.
L'approche présentée dans ce paragraphe vise donc à montrer
que les trous noirs primordiaux pourraient être les seuls objets de l'Univers
contemporain nécessitant un traitement quantique de la gravitation.
Ils représenteraient un laboratoire de physique inespéré. Beaucoup d'aspects de
leur évaporation, en particulier dans la région de Planck, demeurent
extrêmement spéculatifs mais un modèle cohérent commence à émerger. En particulier,
il est important de noter qu'une approche très différente dans son principe, fondée sur
l'évolution de la constante de couplage gravitationnelle sous l'effet du groupe de
renormalisation [73], conduit à des résultats remarquablement similaires à ceux
présentés ici.
L'action gravitationnelle est donc ici supposée décrite par :
où 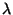 est la constante de couplage de la théorie de cordes sous-jacente. Si l'on
considère que
est la constante de couplage de la théorie de cordes sous-jacente. Si l'on
considère que 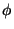 est le champ dilatonique, la fonction de couplage
est le champ dilatonique, la fonction de couplage 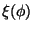 est
fixée par les principes fondamentaux des modèle de cordes et doit s'écrire
[74,75]
est
fixée par les principes fondamentaux des modèle de cordes et doit s'écrire
[74,75] 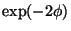 , ce qui conduit à :
, ce qui conduit à :
Partant de ce Lagrangien, une solution de type trou noir statique, à symétrie sphérique
et asymptotiquement plate est recherchée. Pour ce faire, la métrique est
paramétrisée
par [63] :
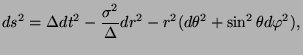 |
|
|
(2.1) |
avec
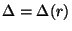 ,
,
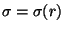 .
Le développement asymptotique des solutions autour de la forme de Schwarzshild s'écrit :
.
Le développement asymptotique des solutions autour de la forme de Schwarzshild s'écrit :
où 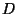 est la charge dilatonique (cf. [63]). Une solution conduisant à un
horizon régulier de type quasi-Schwarzshild est obtenue par simulation numérique
et le comportement au voisinage de l'horizon se paramétrise :
est la charge dilatonique (cf. [63]). Une solution conduisant à un
horizon régulier de type quasi-Schwarzshild est obtenue par simulation numérique
et le comportement au voisinage de l'horizon se paramétrise :
où 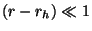 ,
, 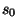 ,
,
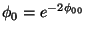 et
et 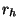 sont trois paramètres
indépendants.
Après résolution des équations au premier ordre de perturbation, on obtient la limite
suivante sur le rayon minimal possible d'un trou noir [63] :
sont trois paramètres
indépendants.
Après résolution des équations au premier ordre de perturbation, on obtient la limite
suivante sur le rayon minimal possible d'un trou noir [63] :
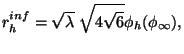 |
|
|
(2.3) |
où 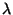 est une combinaison des constantes de couplages (c'est donc un
paramètre fondamental) et
est une combinaison des constantes de couplages (c'est donc un
paramètre fondamental) et
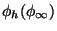 est la valeur du champ de dilaton à
est la valeur du champ de dilaton à
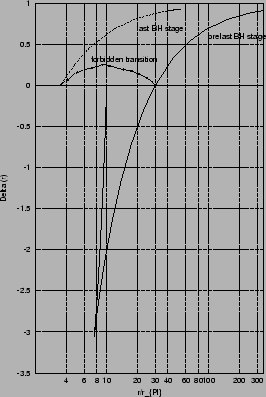
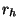 . Ce phénomène est illustré sur la figure 2.3 à gauche pour la fonction
métrique
. Ce phénomène est illustré sur la figure 2.3 à gauche pour la fonction
métrique 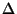 : quand l'horizon devient trop petit la structure des solutions change et
ne conduit plus à une solution de type trou noir.
Des valeurs raisonnables de ces grandeurs (enfin, disons "heuristiquement" raisonnables
car aucune théorie ne peut réellement conduire à des prédictions fiables dans ce
secteur) conduisent à une masse minimale voisine de quelques masses de Planck.
Il est
important de noter que ce résultat est stable sous l'effet de perturbations
temporelles et,
surtout, sous l'effet de l'ajout de termes d'ordres supérieurs en courbure qui peuvent
être calculés analytiquement jusqu'à l'ordre 4 :
: quand l'horizon devient trop petit la structure des solutions change et
ne conduit plus à une solution de type trou noir.
Des valeurs raisonnables de ces grandeurs (enfin, disons "heuristiquement" raisonnables
car aucune théorie ne peut réellement conduire à des prédictions fiables dans ce
secteur) conduisent à une masse minimale voisine de quelques masses de Planck.
Il est
important de noter que ce résultat est stable sous l'effet de perturbations
temporelles et,
surtout, sous l'effet de l'ajout de termes d'ordres supérieurs en courbure qui peuvent
être calculés analytiquement jusqu'à l'ordre 4 :
et
ne changent pas le comportement. Ils correspondent, respectivement, aux
contractions, d'ordre 3 et d'ordre 4 en courbure scalaire,
réalisables à partir du tenseur de Riemann et ne conduisant pas à des
particules "fantômes".
Etant donné que les modifications topologiques associées à ces termes sont
situées à
l'intérieur [76] de l'horizon, elles ne modifient pas la structure des soltutions et n'entrent
pas en conflit avec le résultat précédent. Les simulations numériques montrent que les
termes d'ordres supérieurs augmentent (et donc stabilisent) la valeur de la masse
minimale.
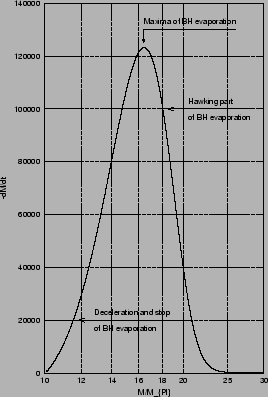
Figure:
Gauche : Illustration d'une transition topologiquement interdite.
Droite : Forme du taux de perte de masse pour un trou noir de Gauss-Bonnet.
|
|
Dans l'approximation WKB, le processus d'évaporation de Hawking est décrit localement
autour de l'horizon. On peut alors utiliser un développement au premier ordre des fonctions
métriques suivant la définition précédemment donnée :
Pour procéder à une évaluation numérique, nous avons procédé à un ajustement des
fonctions simulées par un développement de Taylor en 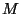 et
et 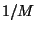 , valide entre
, valide entre
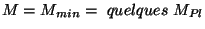 et
et
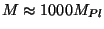 :
:
où (pour
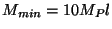 ), les coefficients obtenus sont :
), les coefficients obtenus sont :
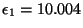 ,
,
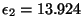 ,
,
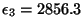 ,
,
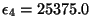 ,
,
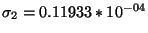 ,
,
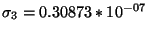 ,
,
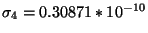 ,
,
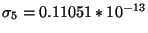 . Ces résultats peuvent maintenant être utilisés pour évaluer le
flux de Hawking modifié dans la région des faibles masses. Suivant l'approche de
[77], on peut calculer la partie imaginaire de l'action (c'est le traitement WKB
de l'effet tunnel) entre les rayons
. Ces résultats peuvent maintenant être utilisés pour évaluer le
flux de Hawking modifié dans la région des faibles masses. Suivant l'approche de
[77], on peut calculer la partie imaginaire de l'action (c'est le traitement WKB
de l'effet tunnel) entre les rayons 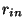 et
et 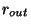 :
:
où 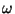 est l'énergie de la particule considérée,
est l'énergie de la particule considérée, 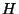 est l'Hamiltonien total et
la métrique est écrite de façon à éviter toute singularité à l'horizon. Nous
utilisons les coordonnées de Painlevé (précisément non divergentes en
est l'Hamiltonien total et
la métrique est écrite de façon à éviter toute singularité à l'horizon. Nous
utilisons les coordonnées de Painlevé (précisément non divergentes en 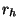 , la
divergence qui apparaît dans les coordonnés de Schwarshlid n'est qu'une singularité
apparente due au système choisi). On peut encore écrire :
, la
divergence qui apparaît dans les coordonnés de Schwarshlid n'est qu'une singularité
apparente due au système choisi). On peut encore écrire :
où 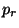 est l'impulsion généralisée. Pour un trou noir de Gauss-Bonnet, les
géodésiques sont données par :
est l'impulsion généralisée. Pour un trou noir de Gauss-Bonnet, les
géodésiques sont données par :
ce qui conduit à :
Après les changements de variables appropriés et un peu d'algèbre, la partie imaginaire
de l'action s'écrit :
Ce qui se simplifie numériquement en :
où 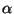 est une expression dont la longueur dépasse quelques pages mais qui se calcule
(heureusement !) très bien par une machine. Pour des valeurs raisonnables de
est une expression dont la longueur dépasse quelques pages mais qui se calcule
(heureusement !) très bien par une machine. Pour des valeurs raisonnables de 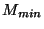 et
en utilisant les développements de Taylor précédement mentionnés, on peut
approximer
et
en utilisant les développements de Taylor précédement mentionnés, on peut
approximer 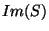 par :
par :
où
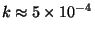 en unités de Planck (cf [61] pour une illustration
de la qualité de l'estimation).
en unités de Planck (cf [61] pour une illustration
de la qualité de l'estimation).
Le spectre différentiel peut alors s'écrire :
où nous avons ajouté à l'approche de [77] une fonction 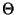 de Heavyside
qui assure la conservation de l'énergie dans le domaine des très faibles masses. Dans
la suite de ce chapitre, j'utilise les unités conventionnelles (SI) et non plus les
unités de Planck dans la mesure ou l'objectif n'est plus maintenant de fixer le cadre
théorique mais d'estimer des valeurs expérimentales. Deux questions doivent ici être
résolues : quels types de champs seront émis (et, corrélativement, quelles fonctions
de couplage
de Heavyside
qui assure la conservation de l'énergie dans le domaine des très faibles masses. Dans
la suite de ce chapitre, j'utilise les unités conventionnelles (SI) et non plus les
unités de Planck dans la mesure ou l'objectif n'est plus maintenant de fixer le cadre
théorique mais d'estimer des valeurs expérimentales. Deux questions doivent ici être
résolues : quels types de champs seront émis (et, corrélativement, quelles fonctions
de couplage 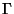 doivent être utilisées) et quelle gamme de masses est physiquement
intéressante ? Pour y répondre, le taux de perte de masse doit être calculé :
doivent être utilisées) et quelle gamme de masses est physiquement
intéressante ? Pour y répondre, le taux de perte de masse doit être calculé :
où l'intégration est menée jusqu'à
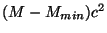 pour s'assurer que la
transition sous
pour s'assurer que la
transition sous 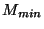 demeure impossible. Les probabilités d'absorption peuvent
clairement être prises dans la limite
demeure impossible. Les probabilités d'absorption peuvent
clairement être prises dans la limite
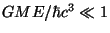 étant donné le cut-off imposé par
étant donné le cut-off imposé par 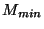 qui empèche
d'atteindre les énergies thermiques de l'ordre de
qui empèche
d'atteindre les énergies thermiques de l'ordre de 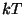 . En utilisant les formules
analytiques des
. En utilisant les formules
analytiques des 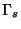 dans l'approximation des faibles énergies [78] et le
développement asymptotique de
dans l'approximation des faibles énergies [78] et le
développement asymptotique de 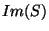 dérivé au paragraphe précédent, on obtient :
dérivé au paragraphe précédent, on obtient :
pour l'émission de particules de spin 1, dont il est aisé de montrer qu'elle domine
celle des particules de spins 1/2 et 2. Il est intéressant de noter que l'émission des
fermions autour de 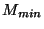 n'est pas considérablement modifiée par le modèle EDGB
(Einstein-Dilaton-Gauss-Bonnet),
étant donné qu'à l'ordre le plus bas,
n'est pas considérablement modifiée par le modèle EDGB
(Einstein-Dilaton-Gauss-Bonnet),
étant donné qu'à l'ordre le plus bas,
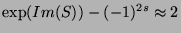 . De plus, si l'on se restreint aux champs sans masse (i.e. à l'émission très proche de
. De plus, si l'on se restreint aux champs sans masse (i.e. à l'émission très proche de 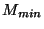 ), le terme EDGB change la nature des
particules les plus abondamment émises des neutrinos aux photons. Le taux de perte de
masse réel est donc simplement le double de celui donné ici pour tenir compte des deux
états d'hélicité du photon.
), le terme EDGB change la nature des
particules les plus abondamment émises des neutrinos aux photons. Le taux de perte de
masse réel est donc simplement le double de celui donné ici pour tenir compte des deux
états d'hélicité du photon.
Avec l'expression obtenue 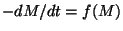 , il est possible de calculer la masse
, il est possible de calculer la masse 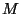 pout
tout temps
pout
tout temps 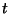 après la formation à la masse initiale
après la formation à la masse initiale 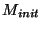 :
:
Comme attendu, le résultat ne dépend pas de 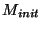 puisque le temps requis pour
passer de
puisque le temps requis pour
passer de 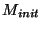 a quelques
a quelques 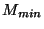 est très petit devant celui nécessaire pour
passer de
est très petit devant celui nécessaire pour
passer de 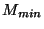 à
à 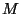 dès que
dès que
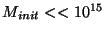 g et
g et
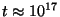 s. Au
temps
s. Au
temps 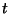 , la masse est donc donnée par :
, la masse est donc donnée par :
Ce qui peut être implémenté dans l'expression du spectre d'émission :
conduisant à une fréquence d'émission de
Quand on applique cette démarche à des reliques de trous noirs
formées dans l'Univers primordial, cela conduit à
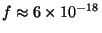 Hz avec
des énergiee typiques de l'ordre de
Hz avec
des énergiee typiques de l'ordre de
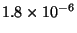 eV. Ce taux d'émission est très
petit (en fait, il est intéressant de noter que la capacité calorifique du trou noir
change de signe !) puisqu'il correspond à une évaporation en photons dont la longueur
d'onde est beaucoup plus grande que le rayon gravitationnel du PBH. Il faut néanmoins
souligner que le spectre présente un comportement monotoniquement croissant (jusqu'au
cutoff) avec une dépendance en
eV. Ce taux d'émission est très
petit (en fait, il est intéressant de noter que la capacité calorifique du trou noir
change de signe !) puisqu'il correspond à une évaporation en photons dont la longueur
d'onde est beaucoup plus grande que le rayon gravitationnel du PBH. Il faut néanmoins
souligner que le spectre présente un comportement monotoniquement croissant (jusqu'au
cutoff) avec une dépendance en 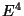 , ce qui est tout-à-fait singulier en
astrophysique (et témoigne du couplage naturel du trou noir). De plus, cela montre que,
bien que de faible intensité, l'évaporation ne s'arrête jamais et décroit en
, ce qui est tout-à-fait singulier en
astrophysique (et témoigne du couplage naturel du trou noir). De plus, cela montre que,
bien que de faible intensité, l'évaporation ne s'arrête jamais et décroit en 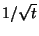 .
La différence entre ce modèle et la vision habituelle (théorie de Hawking simple) est
présentée à la figure 2.3 à droite.
.
La différence entre ce modèle et la vision habituelle (théorie de Hawking simple) est
présentée à la figure 2.3 à droite.
Pour évaluer l'éventuelle détectabilité expérimentale de ce phénomène, nous
définissons : 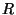 la distance entre la source et l'observateur,
la distance entre la source et l'observateur, 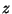 le redshift
correspondant,
le redshift
correspondant, 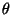 l'angle d'ouverture du détecteur,
l'angle d'ouverture du détecteur,
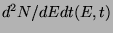 le flux
individuel d'une relique de trou noir (tel qu'évalué dans cette étude) au temps
le flux
individuel d'une relique de trou noir (tel qu'évalué dans cette étude) au temps 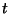 ,
,
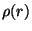 la densité numérique de reliques prenant en compte la dilution due à
l'expansion de l'Univers,
la densité numérique de reliques prenant en compte la dilution due à
l'expansion de l'Univers, 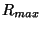 l'horizon cosmologique dans la gamme d'énergie
considérée,
l'horizon cosmologique dans la gamme d'énergie
considérée, 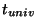 l'âge de l'Univers et
l'âge de l'Univers et 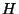 le paramètre de Hubble. Le spectre
"expérimental"
le paramètre de Hubble. Le spectre
"expérimental" 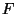 (J
(J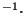 s
s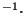 sr
sr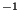 .m
.m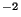 ) s'écrit :
) s'écrit :
ce qui conduit à :
Cette intégrale, qui tient compte à la fois de ce que les reliques formées loin de la
Terre sont à des stades plus précoces de leur évolution (effet vers les hautes
énergies) et de ce que le décalage spectral est plus important (effet vers les basses
énergies) peut être analytiquement calculée. Elle conduit alors, pour
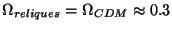 , à
, à
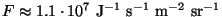 autour
autour 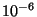 eV, ce qui est extrêmement petit, environ 20
ordres de grandeur en-dessous du fond astrophysique. Ceci ferme la porte à toute
possibilité de mise en évidence directe de l'émission de ces reliques.
Réciproquement, cela ouvre une voie naturelle à les considérer comme un excellent
candidat à la matière noire froide ! L'enjeu de cette étude était néanmoins
avant tout purement théorique et concernait le problème de la fin de vie qui trouve
ici une réponse possible.
eV, ce qui est extrêmement petit, environ 20
ordres de grandeur en-dessous du fond astrophysique. Ceci ferme la porte à toute
possibilité de mise en évidence directe de l'émission de ces reliques.
Réciproquement, cela ouvre une voie naturelle à les considérer comme un excellent
candidat à la matière noire froide ! L'enjeu de cette étude était néanmoins
avant tout purement théorique et concernait le problème de la fin de vie qui trouve
ici une réponse possible.




suivant: Matière noire [79]
monter: Les trous noirs primordiaux
précédent: Univers primordial [45]
Table des matières
Aurelien Barrau
2004-07-01
![]() (comme montré dans le premier paragraphe de ce chapitre),
on voit bien que
(comme montré dans le premier paragraphe de ce chapitre),
on voit bien que
![]() n'est pas définie. De plus, dans cette image, l'évaporation
complète conduirait sans doute à une singularité nue qui contredirait le
principe de censure cosmique de Penrose.
Le formalisme habituel ne peut plus s'appliquer lorsque la masse devient de
l'ordre de la masse de Planck. La description quasi-classique est inadaptée
et les phénomènes de gravité
quantique doivent être pris en compte.
n'est pas définie. De plus, dans cette image, l'évaporation
complète conduirait sans doute à une singularité nue qui contredirait le
principe de censure cosmique de Penrose.
Le formalisme habituel ne peut plus s'appliquer lorsque la masse devient de
l'ordre de la masse de Planck. La description quasi-classique est inadaptée
et les phénomènes de gravité
quantique doivent être pris en compte.
![]() , et nous paramétrons les fonctions
``correctives" par rapport au comportement asymptotique de Schwarzschild. Le taux de perte de
masse présente, dans cette approche, une forme très caractéristique avec un
maximum nettement marqué puis une lente décélération correspondant à la
vie post-mortem du trou noir durant laquelle sa température augmente
mais l'énergie des quanta émis diminue [71]. Intuitivement, on peut comprendre ce
comportement en imaginant que la température correspond en fait à l'énergie
des particules qui se couplent le plus naturellement avec le trou noir (i.e. dont
la longueur d'onde Compton est de l'ordre du rayon gravitationnel). Elle ne peut donc
qu'augmenter au cours de l'évaporation. En revanche, l'énergie moyenne des quanta émis
commence à diminuer à partir du moment où la limite topologique qui impose une masse
minimale en dessous de laquelle le trou noir ne peut pas transiter [72] tronque
la distribution naturelle de probabilité. Tout se passe comme si le trou noir
``essayait"
d'émettre un quantum toute les
, et nous paramétrons les fonctions
``correctives" par rapport au comportement asymptotique de Schwarzschild. Le taux de perte de
masse présente, dans cette approche, une forme très caractéristique avec un
maximum nettement marqué puis une lente décélération correspondant à la
vie post-mortem du trou noir durant laquelle sa température augmente
mais l'énergie des quanta émis diminue [71]. Intuitivement, on peut comprendre ce
comportement en imaginant que la température correspond en fait à l'énergie
des particules qui se couplent le plus naturellement avec le trou noir (i.e. dont
la longueur d'onde Compton est de l'ordre du rayon gravitationnel). Elle ne peut donc
qu'augmenter au cours de l'évaporation. En revanche, l'énergie moyenne des quanta émis
commence à diminuer à partir du moment où la limite topologique qui impose une masse
minimale en dessous de laquelle le trou noir ne peut pas transiter [72] tronque
la distribution naturelle de probabilité. Tout se passe comme si le trou noir
``essayait"
d'émettre un quantum toute les ![]() s (soit 10
s (soit 10 ![]() si l'on
considère, par exemple, que sa masse est
de l'ordre de 10
si l'on
considère, par exemple, que sa masse est
de l'ordre de 10 ![]() ) mais que l'immense majorité du spectre naturel lui était
quantiquement
interdit : seul dans le cas où l'évènement ``tombe" dans la petite portion pour laquelle
l'évaporation peut
avoir lieu (i.e. conduisant à une masse supérieure à la masse minimale), le quantum
est émis et la masse diminue, rendant la prochaine itération moins probable encore et
l'énergie moyenne plus faible.
) mais que l'immense majorité du spectre naturel lui était
quantiquement
interdit : seul dans le cas où l'évènement ``tombe" dans la petite portion pour laquelle
l'évaporation peut
avoir lieu (i.e. conduisant à une masse supérieure à la masse minimale), le quantum
est émis et la masse diminue, rendant la prochaine itération moins probable encore et
l'énergie moyenne plus faible.
![\begin{displaymath}
S = \int d^4 x \sqrt{-g} \Biggl[ - R + 2 \partial_\mu \phi
\partial^\mu \phi
+ \lambda \xi(\phi) S_{GB} + \ldots \Biggr],
\end{displaymath}](img414.png)
![\begin{displaymath}
S = \int d^4 x \sqrt{-g} \Biggl[ - R + 2 \partial_\mu \phi
...
...i \nonumber \\
+ \lambda e^{-2\phi} S_{GB} + \ldots \Biggr].
\end{displaymath}](img417.png)
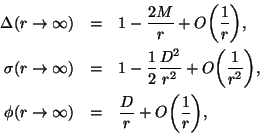
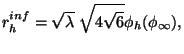
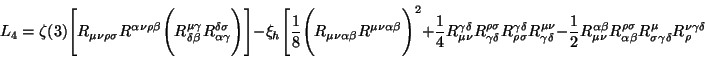
![\begin{displaymath}
- R_{\mu\nu}^{\alpha\beta} R_{\alpha\beta}^{\rho\nu}
R_{\rho...
...beta\sigma\gamma\delta} R_{\delta\gamma\rho}^{\alpha} \Biggr]
\end{displaymath}](img437.png)
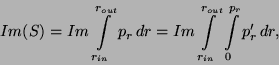
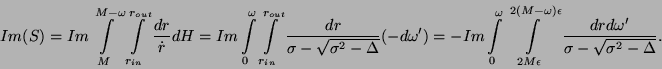
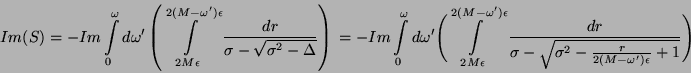
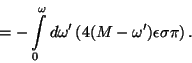
![]() , il est possible de calculer la masse
, il est possible de calculer la masse ![]() pout
tout temps
pout
tout temps ![]() après la formation à la masse initiale
après la formation à la masse initiale ![]() :
:
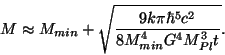
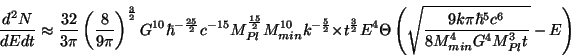
![]() la distance entre la source et l'observateur,
la distance entre la source et l'observateur, ![]() le redshift
correspondant,
le redshift
correspondant, ![]() l'angle d'ouverture du détecteur,
l'angle d'ouverture du détecteur,
![]() le flux
individuel d'une relique de trou noir (tel qu'évalué dans cette étude) au temps
le flux
individuel d'une relique de trou noir (tel qu'évalué dans cette étude) au temps ![]() ,
,
![]() la densité numérique de reliques prenant en compte la dilution due à
l'expansion de l'Univers,
la densité numérique de reliques prenant en compte la dilution due à
l'expansion de l'Univers, ![]() l'horizon cosmologique dans la gamme d'énergie
considérée,
l'horizon cosmologique dans la gamme d'énergie
considérée, ![]() l'âge de l'Univers et
l'âge de l'Univers et ![]() le paramètre de Hubble. Le spectre
"expérimental"
le paramètre de Hubble. Le spectre
"expérimental" ![]() (J
(J![]() s
s![]() sr
sr![]() .m
.m![]() ) s'écrit :
) s'écrit :