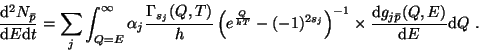Il s'agit ici d'utiliser les limites supérieures précédemment obtenues sur la
densité de trous noirs afin de dériver des contraintes cosmologiques.
Ces dernières concernent des échelles pour lesquelles aucune autre observable n'est
aujourd'hui envisagée et apportent une information nouvelle forte sur les
fluctuations de l'Univers très primordial. Pour étudier ce que l'absence (ou l'extrême
rareté :
![]() ) de petits trous noirs peut nous
révéler sur le Cosmos, il faut s'intéresser aux détails du mécanisme de
formation.
) de petits trous noirs peut nous
révéler sur le Cosmos, il faut s'intéresser aux détails du mécanisme de
formation.
Le modèle cosmologique standard repose aujourd'hui sur une brève phase
d'inflation durant laquelle le facteur d'échelle de l'Univers croît exponentiellement.
Cette image est motivée par la résolution d'un certain nombre de problèmes
liés au modèle classique du Big-Bang (par exemple l'isotropie du fond de rayonnement
cosmologique - CMB - sur des échelles qui semblent pourtant causalement
décorrélées, la
platitude de l'Univers, l'augmentation considérable d'entropie, l'homogénéité à
grande échelle, l'absence de monopôles magnétiques, etc.) mais repose également sur de solides bases de microphysique
(brisure spontanée de symétrie pour un champ scalaire évoluant
lentement à partir d'une position de ``faux vide" vers le minimum autour duquel se produit la
désexcitation dans le modèle de new inflation. En fait les modèles de type
chaotique inflation sont plus généraux encore puisque c'est la valeur du champ
lui-même qui entraîne l'inflation.). Avec la réserve toutefois que le champ en question n'a pas encore été
expérimentalement mis en évidence (ni aucun champ scalaire fondamental d'ailleurs) !
Les modèles d'inflation permettent de générer des spectres de
fluctuations qui rendent convenablement compte des structures dans l'Univers contemporain. Ils
sont généralement proches du type Harrison-Zeldovich, c'est-à-dire invariants d'échelle
(ce qui correspond à
![]() avec
avec ![]() et
et ![]() le nombre d'onde). La production
de trous noirs primordiaux étant associée aux très petites échelles et donc aux grands
nombres d'onde,
seuls les spectres bleus, i.e. avec
le nombre d'onde). La production
de trous noirs primordiaux étant associée aux très petites échelles et donc aux grands
nombres d'onde,
seuls les spectres bleus, i.e. avec ![]() , peuvent produire une quantité appréciable
de trous noirs primordiaux lorsqu'ils sont normalisés aux valeurs connues (sur le CMB ou les
grandes structures). L'idée globale de la production des petits trous noirs est d'augmenter,
quel que soit le moyen, la puissance aux petites échelles. Réciproquement, l'absence
de petits trous noirs est une façon très efficace d'exclure les modèles qui
généreraient un
, peuvent produire une quantité appréciable
de trous noirs primordiaux lorsqu'ils sont normalisés aux valeurs connues (sur le CMB ou les
grandes structures). L'idée globale de la production des petits trous noirs est d'augmenter,
quel que soit le moyen, la puissance aux petites échelles. Réciproquement, l'absence
de petits trous noirs est une façon très efficace d'exclure les modèles qui
généreraient un ![]() important à grand
important à grand ![]() .
Les dernières études combinées des
expériences de mesure du CMB (en particulier Boomerang [46], Maxima
[47], Archeops [48] et, bien-sûr, WMAP [126]) montrent
que l'indice spectral
.
Les dernières études combinées des
expériences de mesure du CMB (en particulier Boomerang [46], Maxima
[47], Archeops [48] et, bien-sûr, WMAP [126]) montrent
que l'indice spectral ![]() est très voisin de 1 :
est très voisin de 1 :
![]() ([50]). Extrapolée
jusqu'aux très grands
([50]). Extrapolée
jusqu'aux très grands ![]() cette valeur ne conduit qu'à une densité extrêmement faible
de trous noirs primordiaux (il faudrait
cette valeur ne conduit qu'à une densité extrêmement faible
de trous noirs primordiaux (il faudrait ![]() pour une contribution
importante des PBH à la matière noire). Il est d'ailleurs très intéressant de
noter que, il y a deux ans, la limite supérieure sur
pour une contribution
importante des PBH à la matière noire). Il est d'ailleurs très intéressant de
noter que, il y a deux ans, la limite supérieure sur ![]() venant des trous noirs
primordiaux (entre 1.24 [51] et 1.30 [52] selon les modèles)
était la meilleure disponible et se trouvait plus contraignante que les mesures de COBE.
Néanmoins, il est tout-à-fait naturel de supposer que le spectre ne demeure pas
une simple loi de puissance
venant des trous noirs
primordiaux (entre 1.24 [51] et 1.30 [52] selon les modèles)
était la meilleure disponible et se trouvait plus contraignante que les mesures de COBE.
Néanmoins, il est tout-à-fait naturel de supposer que le spectre ne demeure pas
une simple loi de puissance
![]() avec
avec ![]() sur des échelles si
éloignées et les trous noirs primordiaux demeurent alors l'unique voie
d'accès à laquelle on peut aujourd'hui penser pour accéder aux petites échelles
(avec les ondes gravitationnelles primordiales dont la détection n'est pas envisagée
dans les cinquante prochaines années). En particulier, le potentiel du champ d'inflaton peut présenter une échelle
caractéristique liée, par exemple, aux énergies des théories de grande unification
(GUT). Ceci conduit naturellement à une brisure d'invariance d'échelle (BSI) dans le spectre
primordial. On s'intéresse ici plus spécifiquement au modèle développé par A.
Starobinsky [53] où un saut dans la dérivée du potentiel interrompt le
processus de roulement lent du champ et entraîne la création de particules et - éventuellement - de
trous noirs primordiaux. Le spectre peut alors être calculé analytiquement et reproduit de façon
convaincante un certain nombre d'observables (dont la présence possible d'une bosse dans le
spectre de puissance de la matière ordinaire) [54]. Il est alors simplement
dépendant de deux paramètres : la hauteur de saut
sur des échelles si
éloignées et les trous noirs primordiaux demeurent alors l'unique voie
d'accès à laquelle on peut aujourd'hui penser pour accéder aux petites échelles
(avec les ondes gravitationnelles primordiales dont la détection n'est pas envisagée
dans les cinquante prochaines années). En particulier, le potentiel du champ d'inflaton peut présenter une échelle
caractéristique liée, par exemple, aux énergies des théories de grande unification
(GUT). Ceci conduit naturellement à une brisure d'invariance d'échelle (BSI) dans le spectre
primordial. On s'intéresse ici plus spécifiquement au modèle développé par A.
Starobinsky [53] où un saut dans la dérivée du potentiel interrompt le
processus de roulement lent du champ et entraîne la création de particules et - éventuellement - de
trous noirs primordiaux. Le spectre peut alors être calculé analytiquement et reproduit de façon
convaincante un certain nombre d'observables (dont la présence possible d'une bosse dans le
spectre de puissance de la matière ordinaire) [54]. Il est alors simplement
dépendant de deux paramètres : la hauteur de saut ![]() et la position
et la position ![]() de
l'échelle caractéristique. Dans une telle
démarche, la production de trous noirs a manifestement lieu autour de cette échelle :
il est donc plus intéressant de considérer ici les trous noirs formés par mécanisme
d'effondrement critique [55]. Comme dans de nombreux phénomènes de physique
statistique, les masses résultantes sont alors données par une relation du type
de
l'échelle caractéristique. Dans une telle
démarche, la production de trous noirs a manifestement lieu autour de cette échelle :
il est donc plus intéressant de considérer ici les trous noirs formés par mécanisme
d'effondrement critique [55]. Comme dans de nombreux phénomènes de physique
statistique, les masses résultantes sont alors données par une relation du type
![]() où
où ![]() est un paramètre de contrôle du système,
est un paramètre de contrôle du système, ![]() est la
valeur critique et
est la
valeur critique et
![]() est l'exposant (universel) du spectre.
est l'exposant (universel) du spectre.
Ce paragraphe présente comment le modèle inflationnaire BSI permet de calculer les grandeurs
nécessaires à l'évaluation du spectre de masse des trous noirs, établit explicitement leur
densité et montre comment les contraintes observationnelles précédentes imposent des
conditions strictes sur les paramètres du modèle.
Un trou noir primordial se forme lorsque le contraste de densité ![]() moyenné sur un
volume dont la taille est égale au rayon de Hubble (
moyenné sur un
volume dont la taille est égale au rayon de Hubble (![]() ) satisfait
) satisfait
![]() , la masse du trou est alors égale à la masse de l'horizon
, la masse du trou est alors égale à la masse de l'horizon ![]() , i.e.
la masse contenue dans un volume de Hubble. La valeur minimale
, i.e.
la masse contenue dans un volume de Hubble. La valeur minimale ![]() se situe, selon
les modèles, entre 1/3 et 0.7 [56]: elle est dictée par le fait que la densité doit être
suffisante pour la création d'un trou noir (l'amplitude de la fluctuation doit surmonter la
pression de Jeans).
se situe, selon
les modèles, entre 1/3 et 0.7 [56]: elle est dictée par le fait que la densité doit être
suffisante pour la création d'un trou noir (l'amplitude de la fluctuation doit surmonter la
pression de Jeans).
Chaque échelle physique ![]() est définie par un nombre d'onde
est définie par un nombre d'onde ![]() qui évolue
avec le temps selon
qui évolue
avec le temps selon
![]() où
où ![]() est le facteur d'échelle de
l'Univers. Pour une échelle donnée, le temps de
``croisement de l'horizon" est conventionnellement donné par
est le facteur d'échelle de
l'Univers. Pour une échelle donnée, le temps de
``croisement de l'horizon" est conventionnellement donné par ![]() tel que
tel que
![]() (on retrouve en effet
(on retrouve en effet
![]() i.e. au rayon de Hubble). Il
s'agit du temps auquel l'échelle considérée ré-entre dans le rayon de Hubble (après
en être sortie durant l'inflation) : compte-tenu de ce qu'à l'issue de l'inflation le
facteur d'échelle croît moins vite que l'horizon, ceci finit nécessairement par avoir
lieu. C'est à cet instant
i.e. au rayon de Hubble). Il
s'agit du temps auquel l'échelle considérée ré-entre dans le rayon de Hubble (après
en être sortie durant l'inflation) : compte-tenu de ce qu'à l'issue de l'inflation le
facteur d'échelle croît moins vite que l'horizon, ceci finit nécessairement par avoir
lieu. C'est à cet instant ![]() qu'un trou noir de masse voisine de
qu'un trou noir de masse voisine de ![]() peut se former :
les différentes ``zones" de la fluctuation sont en contact causal et l'effondrement peut
se produire. Il y a alors une correspondance biunivoque entre
peut se former :
les différentes ``zones" de la fluctuation sont en contact causal et l'effondrement peut
se produire. Il y a alors une correspondance biunivoque entre ![]() ,
, ![]() et
et
![]() . Il est aussi possible d'établir cette correspondance à n'importe quel autre temps
. Il est aussi possible d'établir cette correspondance à n'importe quel autre temps
![]() et de relier les quantités physiques à l'instant
et de relier les quantités physiques à l'instant ![]() à leurs valeurs à
à leurs valeurs à ![]() .
.
Si les fluctuations primordiales obéissent à une statistique gaussienne, la densité de
probabilité pour le contraste de densité ![]() moyenné sur une sphère de rayon
moyenné sur une sphère de rayon ![]() est donnée par :
est donnée par :
La démarche ici présentée se fonde sur ce formalisme et tient compte de ce que le spectre de
puissance doit être évalué correctement, c'est-à-dire à l'aide d'une fonction de transfert
qui décrit son évolution [58]. La densité de trous noirs primordiaux est ainsi
calculée de façon exacte et normalisée aux fluctuations du fond cosmologique,
ce qui permet de traduire les contraintes observationnelles en contraintes physiques sur
le modèle. Nous présentons ainsi les flux d'antiprotons propagés dans la Galaxie et,
en demandant qu'ils demeurent inférieurs (moyennant, bien-sûr, une étude statistique sur les
erreurs) aux spectres mesurés, nous obtenons une limite supérieure sur la fraction de masse de
l'Univers ayant subi un effondrement en trou noir. La valeur très faible de
celle-ci (
![]() ), et donc très
intéressante, obtenue à des échelles de l'ordre de
), et donc très
intéressante, obtenue à des échelles de l'ordre de ![]() g est
nettement plus petite que
la valeur de
g est
nettement plus petite que
la valeur de ![]() donnée dans les chapitres précédents. Ceci simplement parce que la
mesure est ici obtenue directement au moment de la formation, dans un Univers largement dominé
par le rayonnement et dans lequel les trous noirs ont donc été nettement moins dilués que les
photons environnants (facteur
donnée dans les chapitres précédents. Ceci simplement parce que la
mesure est ici obtenue directement au moment de la formation, dans un Univers largement dominé
par le rayonnement et dans lequel les trous noirs ont donc été nettement moins dilués que les
photons environnants (facteur ![]() supplémentaire pour les modes électromagnétiques à cause
du redshift). Nous donnons ensuite la traduction de ces résultats en termes d'amplitude de
la brisure d'invariance dans le spectre de fluctuations primordial (pour différents modèles de
formation et différentes valeurs de la constante cosmologique) et montrons qu'il ne peut y avoir
trop de puissance à ces échelles.
supplémentaire pour les modes électromagnétiques à cause
du redshift). Nous donnons ensuite la traduction de ces résultats en termes d'amplitude de
la brisure d'invariance dans le spectre de fluctuations primordial (pour différents modèles de
formation et différentes valeurs de la constante cosmologique) et montrons qu'il ne peut y avoir
trop de puissance à ces échelles.
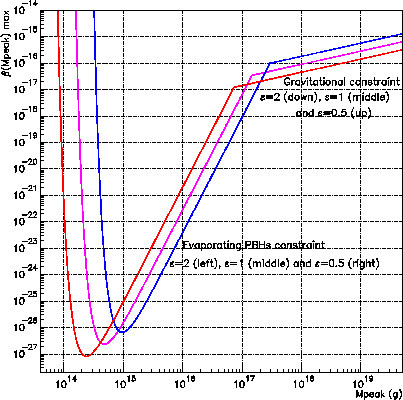
Un étude quantitative des contraintes cosmologiques associées à l'absence de détection
de trous noirs primordiaux requiert un calcul précis du spectre de masse des trous noirs.
Nous nous plaçons donc ici dans le cadre d'une formation par processus quasi-critique [59]
en présence d'une échelle caractéristique dans le spectre primordial [60]. La
formation a ainsi lieu à des masses ![]() voisines de
voisines de
![]() ,
la masse de l'horizon au temps
,
la masse de l'horizon au temps ![]() de croisement de l'horizon - le
temps
de croisement de l'horizon - le
temps ![]() étant défini par
étant défini par
![]() . La formation suit alors la loi [59]
. La formation suit alors la loi [59]
![\begin{displaymath}\frac{d\Omega_{PBH}}{d\ln M}\equiv \frac{d \Omega_{PBH}(M,t_{...
... \frac{M}{M_{peak}}\right )^{1+\frac{1}{\gamma}} p[\delta(M)].
\end{displaymath}](img374.png)
![\begin{displaymath}\frac{d \Omega_{PBH}}{d\ln M} = \epsilon^{-\frac{1}{\gamma}}~...
...left ( \frac{M}{M_{peak}}\right )^{\frac{1}{\gamma}}\Biggr ]~,
\end{displaymath}](img376.png)
![]() donne la probabilité qu'une région
de taille comobile
donne la probabilité qu'une région
de taille comobile
![]() ait un constraste de densité moyenné
au temps
ait un constraste de densité moyenné
au temps ![]() dans la gamme
dans la gamme
![]()
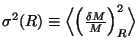 est calculé avec la fonction fenêtre décrite
précédemment. Généralement, on appelle spectre primordial le spectre aux échelles
"au-delà" de l'horizon à l'issue de l'inflation. Dans ce cas, la dépendance d'échelle
des modes considérés n'est pas affectée par l'évolution cosmologique. Néanmoins,
pour des échelles "dans" l'horizon, cela n'est plus juste et il faut tenir compte de ce que:
est calculé avec la fonction fenêtre décrite
précédemment. Généralement, on appelle spectre primordial le spectre aux échelles
"au-delà" de l'horizon à l'issue de l'inflation. Dans ce cas, la dépendance d'échelle
des modes considérés n'est pas affectée par l'évolution cosmologique. Néanmoins,
pour des échelles "dans" l'horizon, cela n'est plus juste et il faut tenir compte de ce que:
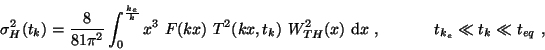
![\begin{displaymath}T^2(kx,t_k)\equiv \Biggl[\frac{9}{x^2}\left(\frac{\sin(c_s x)...
...]^2= W^2_{TH}(c_sx)= W^2_{TH}\left(\frac{x}{\sqrt{3}}\right)~,
\end{displaymath}](img390.png)
Pour un spectre de fluctuations primordiales d'origine inflationnaire normalisé aux grandes
échelles en utilisant le CMB, les quantités ![]() et
et
![]() peuvent
être calculées numériquement. Les valeurs de
peuvent
être calculées numériquement. Les valeurs de ![]() et
et ![]() sont, quant-à
elles, obtenues par simulation pour le spectre particulier considéré.
sont, quant-à
elles, obtenues par simulation pour le spectre particulier considéré.
|
|
|
Une fois les paramètres du modèle ainsi fixés et les observables calculées, nous en
déduisons le spectre de PBH aujourd'hui :