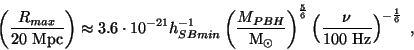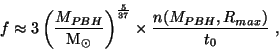Ce chapitre (re)considère les trous noirs primordiaux (pas nécessairement dans le
cadre de l'approche EDGB présentée ci-dessus, mais en toute généralité)
comme candidats à la matière
noire froide dans le contexte des modèles cosmologiques présentant une brisure
d'invariance d'échelle dans le spectre de puissance primordial, c'est-à-dire en
relâchant la contrainte habituelle ![]() . Des approches
analytiques permettent de lier directement et simplement la singularité du
potentiel du champ d'inflaton aux caractéristiques du spectre [53] et
rendent bien compte d'un certain nombre d'observations [54] tout en
généralisant les conditions canoniques des modèles inflationnaires
[53]. Les résultats que nous présentons ici ne sont pas en
contradiction avec les valeurs très faibles (
. Des approches
analytiques permettent de lier directement et simplement la singularité du
potentiel du champ d'inflaton aux caractéristiques du spectre [53] et
rendent bien compte d'un certain nombre d'observations [54] tout en
généralisant les conditions canoniques des modèles inflationnaires
[53]. Les résultats que nous présentons ici ne sont pas en
contradiction avec les valeurs très faibles (
![]() )
données dans le chapitre ``Comment traquer les trous noirs primordiaux".
En effet, celles-ci résultaient d'une grande sensibilité observationnelle
aux trous noirs dont la masse se situe autour de
)
données dans le chapitre ``Comment traquer les trous noirs primordiaux".
En effet, celles-ci résultaient d'une grande sensibilité observationnelle
aux trous noirs dont la masse se situe autour de
![]() g. Nous nous intéressons
maintenant au cas où le spectre de masse des trous noirs permet d'échapper à
cette limite. L'étude précédente garde néanmoins tout-à-fait son sens à
partir du moment où on la considère comme une mesure locale autour de
g. Nous nous intéressons
maintenant au cas où le spectre de masse des trous noirs permet d'échapper à
cette limite. L'étude précédente garde néanmoins tout-à-fait son sens à
partir du moment où on la considère comme une mesure locale autour de ![]() . Les
contraintes cosmologiques qui en résultaient (paragraphe ``Univers primordial") sont donc valides et indépendantes des considérations ici
présentées.
. Les
contraintes cosmologiques qui en résultaient (paragraphe ``Univers primordial") sont donc valides et indépendantes des considérations ici
présentées.
Dans un premier temps, nous prenons en compte la limite supérieure sur la
température de ``reheating" dérivée de la désintégration des gravitinos. En
effet, dans les modèles supersymétriques de type mSUGRA (où la brisure
spontanée de supersymétrie a lieu dans un secteur caché qui communique avec le
secteur visible par la gravité uniquement), la masse du gravitino est attendue dans
la gamme 100 GeV - 1 TeV (i.e. autour de l'échelle électrofaible)
[81]. Or, dans ce cas, les gravitinos produits dans le bain thermique à
l'issue de l'inflation vont se désintégrer en photons (et photinos) dont le nombre
et l'énergie entrent en conflit avec la nucléosynthèse (voir, par exemple
[82] ou [84] pour des revues). Pour échapper à ce problème
(à l'origine d'un grand nombre de développements dans les théories
inflationnaires), la température de reheating doit être inférieure à
environ ![]() GeV (cette limite peut être légèrement relâchée si l'on
considère que le rapport de branchement des gravitinos en photons n'est pas
unitaire, mais elle demeure dans cet ordre de grandeur).
GeV (cette limite peut être légèrement relâchée si l'on
considère que le rapport de branchement des gravitinos en photons n'est pas
unitaire, mais elle demeure dans cet ordre de grandeur).
Or, cette limite se traduit par une masse de l'horizon ![]() à la fin de l'inflation
relativement grande, en tous cas plus grande que
à la fin de l'inflation
relativement grande, en tous cas plus grande que ![]() . Les trous noirs primordiaux
éventuellement formés avant l'inflation étant aujourd'hui en quantités
négligeables à cause de la dilution exponentielle, il en résulte que leur spectre
de masse, quelle que soit sa forme, doit être coupé en dessous de
. Les trous noirs primordiaux
éventuellement formés avant l'inflation étant aujourd'hui en quantités
négligeables à cause de la dilution exponentielle, il en résulte que leur spectre
de masse, quelle que soit sa forme, doit être coupé en dessous de ![]() . Les
limites émanant de la détection des gammas et antiprotons sont donc naturellement
évitées sans recourir à un subterfuge.
En utilisant le formalisme développé au chapitre 2.1 de ce mémoire et le lien entre
la densité totale et la fraction de masse [52]
. Les
limites émanant de la détection des gammas et antiprotons sont donc naturellement
évitées sans recourir à un subterfuge.
En utilisant le formalisme développé au chapitre 2.1 de ce mémoire et le lien entre
la densité totale et la fraction de masse [52]
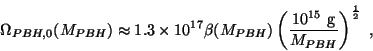
![\begin{displaymath}p\approx\frac{\sigma_{H}^{COBE}}{\delta_{min}}\sqrt{LW\left\{...
...H,0}^2}\left[ \frac{10^{15}~{\rm g}}{M_{H,e}} \right]\right\}},\end{displaymath}](img509.png)
Intéressons nous maintenant au cas où la limite supérieure sur la
température de reheating n'est pas prise en compte. Cela est cohérent dans
les modèles d'inflation thermique ou si, plus simplement, on ignore les modèles supersymétriques qui
résistent toujours à toute mise en évidence expérimentale ! Dans ce cadre, où
l'échelle d'énergie naturelle de l'inflation est haute (et pourrait être signée
dans les années à venir par la présence de mode polarisé B dans le fond de rayonnement
cosmologique [85]), il est nécessaire ``d'ajuster" les paramètres plus précisément
pour éviter que les rayons cosmiques énergétiques émis par les trous
noirs peu
massifs (et donc en évaporation intense) n'entrent en conflit, eux-mêmes, avec la
production d'éléments fragiles (deutérium par exemple) observés. Ce sont ici, non
plus les trous noirs mais les reliques (cf section précédente) qui pourraient
contribuer à la matière noire. Avec [79] la relation
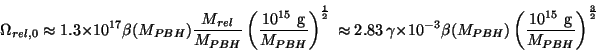
![\begin{displaymath}p\approx\frac{\sigma_{H}^{COBE}}{\delta_{min}}\sqrt{LW\left\{...
...]^2
\left[ \frac{10^{15}~{\rm g}}{M_{H,e}} \right]^3\right\}}.
\end{displaymath}](img529.png)
Il apparaît donc clairement que dans chaque cas (échelle d'inflation haute ou
échelle d'inflation basse) et pour des raisons différentes, un très large espace de
paramètres ici quantifié permet, contrairement à ce qui est souvent pensé, aux trous noirs
primordiaux d'être d'excellents candidats à la matière noire. Mais pour que cette
hypothèse soit véritablement viable, il faut deux points supplémentaires : la
qu'elle soit naturelle et qu'elle soit vérifiable. Je n'ai aucun argument concernant le premier point :
un modèle microphysique d'inflation, non encore clairement construit,
est nécessaire pour aller plus loin dans cette
direction. Le second, en revanche, peut être étudié. Le voie habituelle pour sonder
les trous noirs primordiaux, leur émission de Hawking, n'est ici d'aucun secours puisque,
précisément, le modèle permet d'éviter une production importante de PBH dans la
zone "sensible" (
![]() ). Nous proposons d'utiliser les
ondes gravitationnelles émises par la coalescence de tels trous noirs [86].
Bien-sûr, ces objets sont aujourd'hui très dilués et c'est dans l'Univers primordial
qu'ils doivent avoir formé des systèmes liés. On s'intéresse en fait à la
probabilité que la coalescence de ces systèmes s'achève maintenant. Il faut d'abord calculer la distance
maximale
). Nous proposons d'utiliser les
ondes gravitationnelles émises par la coalescence de tels trous noirs [86].
Bien-sûr, ces objets sont aujourd'hui très dilués et c'est dans l'Univers primordial
qu'ils doivent avoir formé des systèmes liés. On s'intéresse en fait à la
probabilité que la coalescence de ces systèmes s'achève maintenant. Il faut d'abord calculer la distance
maximale ![]() entre la Terre et un système binaire compatible avec la sensibilité d'un
détecteur :
entre la Terre et un système binaire compatible avec la sensibilité d'un
détecteur :