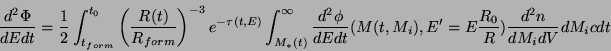
Nous avons reconsidéré l'émission gamma et les contraintes qui en résultent de façon à tenir compte de nouveaux développements [33]. Le flux au niveau de la Terre peut s'écrire :
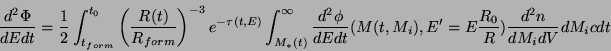
où ![]() est l'époque de formation,
est l'époque de formation, ![]() est l'âge de l'Univers,
est l'âge de l'Univers,
![]() est la profondeur optique,
est la profondeur optique, ![]() est le facteur d'échelle au temps
est le facteur d'échelle au temps
![]() ,
, ![]() est le facteur d'échelle au temps
de la formation,
est le facteur d'échelle au temps
de la formation, ![]() est le flux individuel d'un trou noir en gammas,
est le flux individuel d'un trou noir en gammas, ![]() est la
masse initiale d'un trou dont le temps de vie est
est la
masse initiale d'un trou dont le temps de vie est ![]() et
et ![]() est le spectre de masse initial. Cette relation tient compte de différents
effets :
est le spectre de masse initial. Cette relation tient compte de différents
effets :
Lorsqu'on tient compte à la fois de l'émission directe et de l'émission
indirecte, cela se
traduit pour le spectre mesuré au niveau de la Terre, en fonction de la
densité de trous noirs primordiaux, par [34]:
Cette approche peut être raffinée si l'on tient compte, comme nous
l'avons fait pour les antiprotons, du fond gamma attendu puisque le résultat
précédent se cantonne à requérir un flux venant des trous noirs
primordiaux inférieur au flux expérimentalement mesuré, sans tenir compte
des sources connues. En évaluant la contribution venant des blazars non
résolus et de l'émission des galaxies, Pavlidou & Fields [36] ont
estimé la contribution extra-galactique minimale au fond diffus gamma à 100
MeV. La première a été calculée en utilisant le modèle de
Stecker-Salamon et la seconde est supposée proportionnelle au taux de
formation des étoiles massives (qui est, lui-même, proportionnel au taux
d'explosion des supernovae) puisqu'il est dû aux interactions des rayons
cosmiques avec le gaz diffus. Ce fond vaut, à 100 MeV :
![]() . Nous demandons donc
. Nous demandons donc
![]() , où
, où ![]() est le flux mesuré
à 100 MeV [37], pour obtenir une nouvelle limite supérieure
sur le flux des trous noirs, qu'il est possible de traduire en une limite
supérieure sur leur densité. Afin
d'évaluer celle-ci de façon conservative, la normalisation et l'indice
spectral des ajustements du flux mesuré d'EGRET sont choisis (dans les barres
d'erreurs) de façon à conduire au flux maximum :
est le flux mesuré
à 100 MeV [37], pour obtenir une nouvelle limite supérieure
sur le flux des trous noirs, qu'il est possible de traduire en une limite
supérieure sur leur densité. Afin
d'évaluer celle-ci de façon conservative, la normalisation et l'indice
spectral des ajustements du flux mesuré d'EGRET sont choisis (dans les barres
d'erreurs) de façon à conduire au flux maximum :
![]() . Cela conduit
à :
. Cela conduit
à :
![]() , ce qui constitue la meilleure
limite sur la densité de trous noirs primordiaux actuellement disponible,
quel que soit le canal choisi. Cette valeur est assez proche de celle obtenue
dans l'étude consacrée aux antiprotons et présentée dans le chapitre
précédent. Elle est néanmoins complémentaire car elle repose sur des
phénomènes physiques dans une large mesure indépendants : les gammas ici
considérés ne sont plus piégés dans la galaxie mais intégrés
jusqu'à une fraction considérable du rayon de Hubble et la gamme de masse
prépondérante est légèrement plus grande (la masse des pions neutres étant
inférieure à celle des protons, le température nécessaire pour les produire est
inférieure).
, ce qui constitue la meilleure
limite sur la densité de trous noirs primordiaux actuellement disponible,
quel que soit le canal choisi. Cette valeur est assez proche de celle obtenue
dans l'étude consacrée aux antiprotons et présentée dans le chapitre
précédent. Elle est néanmoins complémentaire car elle repose sur des
phénomènes physiques dans une large mesure indépendants : les gammas ici
considérés ne sont plus piégés dans la galaxie mais intégrés
jusqu'à une fraction considérable du rayon de Hubble et la gamme de masse
prépondérante est légèrement plus grande (la masse des pions neutres étant
inférieure à celle des protons, le température nécessaire pour les produire est
inférieure).
Il sera montré ultérieurement que ces limites supérieures peuvent se traduire
en termes de limites sur la fraction de masse de l'Univers subissant un
effondrement en trou noir. Avec le formalisme exposé dans le paragraphe
``Univers primordial", la
valeur de ![]() ici dérivée se traduit par :
ici dérivée se traduit par :
![]() où :
où :