L'une des améliorations possibles, probablement importante à mettre en oeuvre
dans un avenir proche, consisterait certainement à changer la définition du
![]() préalablement donnée. Il serait en effet intéressant de
modéliser les fluctuations de façon plus détaillée pour tenir compte de
5 origines différentes:
préalablement donnée. Il serait en effet intéressant de
modéliser les fluctuations de façon plus détaillée pour tenir compte de
5 origines différentes:
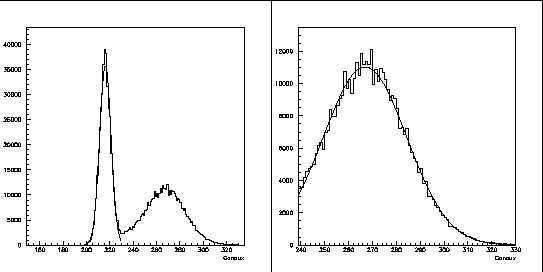 ns). Le
théorème de Wiener-Khinchine assure que la bande passante
importante et la large capacité permettent de traiter la variance
de cette façon.
ns). Le
théorème de Wiener-Khinchine assure que la bande passante
importante et la large capacité permettent de traiter la variance
de cette façon.
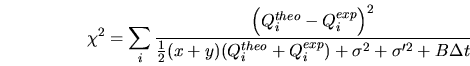 avec l'énergie et le paramètre d'impact. Mais cette nouvelle
définition ne permet pas de changer la valeur de
avec l'énergie et le paramètre d'impact. Mais cette nouvelle
définition ne permet pas de changer la valeur de 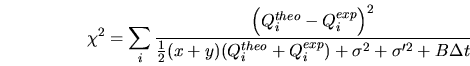 sans changer le
point de convergence, comme c'était le cas précédemment. Il est donc
préférable de tenir compte de cet effet en utilisant les estimateurs
sans changer le
point de convergence, comme c'était le cas précédemment. Il est donc
préférable de tenir compte de cet effet en utilisant les estimateurs
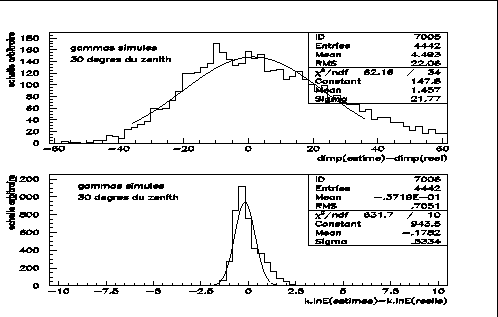 et
et
Les 54 photomultiplicateurs de garde n'ont été installés qu'en juin 1997. Ils
ne sont pas pris en compte dans les résultats présentés ici. Leur insertion
dans l'analyse n'est pas simple car le régime de collection de lumière change.
Pour des images de gerbes électromagnétiques, la lumière attendue dans un
pixel n'est effectivement pas nécessairement proportionnelle à sa surface (elle
varie quadratiquement avec le rayon si celui-ci est plus petit que la largeur de
l'image, linéairement s'il est compris entre la largeur et la longueur et ne
varie plus du tout s'il est plus grand que la longueur). Pour les pixels de garde,
les simulations montrent qu'il convient de considérer,
en moyenne, un gain de lumière d'un facteur 2.7 par rapport aux pixels
internes, c'est-à-dire un peu moins que le rapport des diamètres (![]() 3.3). Cela permet d'obtenir
une reconstruction d'énergie non biaisée mais le gain en résolution est
très faible: les images touchant substantiellement les photomultiplicateurs de
garde touchent aussi plusieurs dizaines de photomultiplicateurs internes et le
maximum de vraisemblance n'est guère mieux contraint par quelques degrés de
liberté supplémentaires. Néanmoins, les paramètres de départ de la
minimisation de
3.3). Cela permet d'obtenir
une reconstruction d'énergie non biaisée mais le gain en résolution est
très faible: les images touchant substantiellement les photomultiplicateurs de
garde touchent aussi plusieurs dizaines de photomultiplicateurs internes et le
maximum de vraisemblance n'est guère mieux contraint par quelques degrés de
liberté supplémentaires. Néanmoins, les paramètres de départ de la
minimisation de ![]() sont évalués à l'aide de la charge totale de l'image
et cette dernière est largement changée (+26% pour des gammas simulés de
8 TeV) par
l'inclusion des pixels de garde. Il est ainsi possible d'améliorer l'évaluation
des conditions initiales et de réduire tout risque de biais. De plus, il
apparaît que l'angle de pointé
sont évalués à l'aide de la charge totale de l'image
et cette dernière est largement changée (+26% pour des gammas simulés de
8 TeV) par
l'inclusion des pixels de garde. Il est ainsi possible d'améliorer l'évaluation
des conditions initiales et de réduire tout risque de biais. De plus, il
apparaît que l'angle de pointé ![]() est mieux reconstruit. Le nombre
de gammas gagnés dans les 5 premiers degrés est de 8% à 8 TeV. La prise en
compte complète de ces photomultiplicateurs est encore à l'étude et il
conviendrait en particulier de calculer la lumière attendue dans le modèle de
façon plus fine, c'est-à-dire en divisant la surface du pixel en plusieurs
surfaces élémentaires permettant d'éviter le recours à une moyenne trop
approximative.
est mieux reconstruit. Le nombre
de gammas gagnés dans les 5 premiers degrés est de 8% à 8 TeV. La prise en
compte complète de ces photomultiplicateurs est encore à l'étude et il
conviendrait en particulier de calculer la lumière attendue dans le modèle de
façon plus fine, c'est-à-dire en divisant la surface du pixel en plusieurs
surfaces élémentaires permettant d'éviter le recours à une moyenne trop
approximative.
Une caractéristique remarquable de l'expérience réside dans le fait que le bruit
électronique est globalement dominant par rapport au bruit de fond de ciel grâce
à l'emploi de la porte analogique rapide qui diminue drastiquement les
photoélectrons de pollution lumineuse. La réduction éventuelle de la
composante électronique serait intéressante mais n'est pas simple dans la
mesure où la largeur des piedestaux obtenus en porte large (![]() 44 ns)
est peu différente de celle des piedestaux obtenus en porte étroite
(
44 ns)
est peu différente de celle des piedestaux obtenus en porte étroite
(![]() 13 ns):
13 ns):
![]() .
Cela signifie que l'origine majeure de ce bruit se trouve probablement au
niveau de l'amplificateur (Burr Brown), après la porte analogique. Il est
également envisageable que la commutation du switch (porte analogique
rapide) induise, par elle-même, un bruit électronique. Les cables plats
assurant la liaison vers les ADC peuvent également dégrader le signal.
La réduction de cette composante nécessite donc une étude qui n'a pas encore
été entreprise et qui n'est certainement pas simple.
.
Cela signifie que l'origine majeure de ce bruit se trouve probablement au
niveau de l'amplificateur (Burr Brown), après la porte analogique. Il est
également envisageable que la commutation du switch (porte analogique
rapide) induise, par elle-même, un bruit électronique. Les cables plats
assurant la liaison vers les ADC peuvent également dégrader le signal.
La réduction de cette composante nécessite donc une étude qui n'a pas encore
été entreprise et qui n'est certainement pas simple.
La technique de maximum de vraisemblance, testée ici pour la première fois
sur des données réelles et des simulations complètes, montre de bonnes
performances lorsqu'elle
est associée à de très fins pixels. Il est néanmoins probable que des
améliorations soient encore possibles, en particulier dans le traitement des
cascades proche du seuil (
![]() GeV), de très haute énergie
(
GeV), de très haute énergie
( 10 TeV) ou de basse élévation (angle zénithal
10 TeV) ou de basse élévation (angle zénithal 
![]() ).
).