



Next: Mesure du bruit de
Up: Piedestaux
Previous: Principe de mesure
Contents
Afin de vérifier que les effets réels des liaisons capacitives sont bien
conformes aux attentes, le bruit de fond de ciel a été simulé. En premier lieu,
l'impulsion à la sortie de l'amplificateur OPA623 (figure 4.19) a été modélisée sous la
forme
où 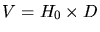 est la
tension,
est la
tension, 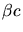 le temps,
le temps,  et
et 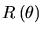 des constantes. On détermine alors ces
trois constantes en imposant la charge
des constantes. On détermine alors ces
trois constantes en imposant la charge
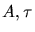 (avec
(avec 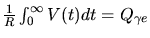 la charge d'un photoélectron), l'amplitude
la charge d'un photoélectron), l'amplitude
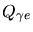 (avec
(avec 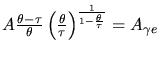 l'amplitude d'un photoélectron) et le temps de montée
l'amplitude d'un photoélectron) et le temps de montée
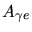 . Pour prendre en compte l'effet de peau au cours du transport
du signal par les 25 mètres de câble (non uniformité de la répartition
surfacique du courant pour les phénomènes transitoires), les valeurs numériques
choisies correspondent à une impulsion moins rapide.
. Pour prendre en compte l'effet de peau au cours du transport
du signal par les 25 mètres de câble (non uniformité de la répartition
surfacique du courant pour les phénomènes transitoires), les valeurs numériques
choisies correspondent à une impulsion moins rapide.
L'impulsion ainsi modélisée, la liaison capacitive est prise en compte sous la
forme d'une équation différentielle élémentaire
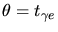 avec
avec 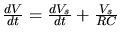 la tension après le
condensateur. L'intégration conduit à une impulsion:
la tension après le
condensateur. L'intégration conduit à une impulsion:
L'effet du bruit de fond de ciel est alors pris en compte en tirant des photons en loi de
Poisson jusqu'à 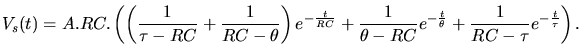 avant l'ouverture de la porte analogique rapide. De plus,
une fluctuation gaussienne de la réponse au photoélectron (
avant l'ouverture de la porte analogique rapide. De plus,
une fluctuation gaussienne de la réponse au photoélectron (
 ) est
également ajoutée. Il apparaît alors un double effet: le pic lui-même, c'est
à dire le piedestal apparent, se déplace vers la gauche (contribution des "queues"
d'impulsions) et s'élargit vers la droite (contribution de la partie "rapide" des
impulsions).
) est
également ajoutée. Il apparaît alors un double effet: le pic lui-même, c'est
à dire le piedestal apparent, se déplace vers la gauche (contribution des "queues"
d'impulsions) et s'élargit vers la droite (contribution de la partie "rapide" des
impulsions).




Next: Mesure du bruit de
Up: Piedestaux
Previous: Principe de mesure
Contents
Aurelien Barrau
2004-07-01
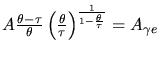 l'amplitude d'un photoélectron) et le temps de montée
l'amplitude d'un photoélectron) et le temps de montée
![]() avec
avec ![]() la tension après le
condensateur. L'intégration conduit à une impulsion:
la tension après le
condensateur. L'intégration conduit à une impulsion: