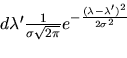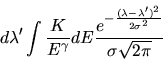Next: Création de paires et
Up: Détection du noyau actif
Previous: Contraintes cosmologiques
Contents
Soit un spectre physique différentiel
où  est le nombre de gammas par unité de surface et par unité
de temps dans l'intervalle d'énergie
est le nombre de gammas par unité de surface et par unité
de temps dans l'intervalle d'énergie 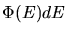 , K une constante et
, K une constante et 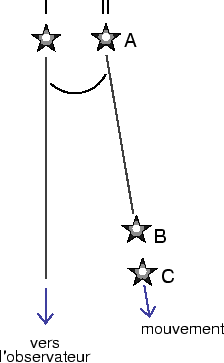 l'indice spectral différentiel.
l'indice spectral différentiel.
La variable
 , où
, où 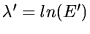 est l'énergie mesurée, est distribuée
gaussiennement autour de
est l'énergie mesurée, est distribuée
gaussiennement autour de 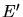 , où
, où 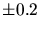 est l'énergie vraie, avec un
écart type
est l'énergie vraie, avec un
écart type 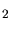 . La conservation des probabilités permet décrire la
loi en
. La conservation des probabilités permet décrire la
loi en 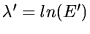 ou en
ou en 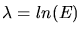 de façon formellement identique. La
distribution connue (gaussienne) étant celle de
de façon formellement identique. La
distribution connue (gaussienne) étant celle de 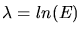 , le terme
correspondant s'écrit
, le terme
correspondant s'écrit
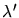 . Il reste à sommer sur la
variable qu'on ne connait pas, c'est-à-dire
. Il reste à sommer sur la
variable qu'on ne connait pas, c'est-à-dire 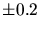 , distibuée en loi de
puissance. Soit:
, distibuée en loi de
puissance. Soit:
Ce qui s'écrit dans les notations utilisées
Le binôme dans l'exponentielle vaut (au signe près):
Et après intégration de la gaussienne correspondant au premier terme, on obtient:
puisque
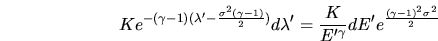 . Le spectre en
énergie mesurée est donc:
. Le spectre en
énergie mesurée est donc:




Next: Création de paires et
Up: Détection du noyau actif
Previous: Contraintes cosmologiques
Contents
Aurelien Barrau
2004-07-01
 l'indice spectral différentiel.
l'indice spectral différentiel.
![]() , où
, où ![]() est l'énergie mesurée, est distribuée
gaussiennement autour de
est l'énergie mesurée, est distribuée
gaussiennement autour de ![]() , où
, où ![]() est l'énergie vraie, avec un
écart type
est l'énergie vraie, avec un
écart type ![]() . La conservation des probabilités permet décrire la
loi en
. La conservation des probabilités permet décrire la
loi en ![]() ou en
ou en ![]() de façon formellement identique. La
distribution connue (gaussienne) étant celle de
de façon formellement identique. La
distribution connue (gaussienne) étant celle de ![]() , le terme
correspondant s'écrit
, le terme
correspondant s'écrit
![]() . Il reste à sommer sur la
variable qu'on ne connait pas, c'est-à-dire
. Il reste à sommer sur la
variable qu'on ne connait pas, c'est-à-dire ![]() , distibuée en loi de
puissance. Soit:
, distibuée en loi de
puissance. Soit: