 varie donc comme
varie donc comme Le gaz qui tombe sur le trou noir central de l'AGN se déplace probablement à des vitesses supersoniques. Des ondes de choc peuvent alors facilement se former et agir comme des accélérateurs efficaces pour les particules présentes, en particulier par le processus de Fermi du premier ordre.
Un front d'onde de choc peut être assimilé à une discontinuité plane
stationnaire qui diminue la vitesse du fluide de ![]() à
à ![]() où
où ![]() est le
rapport de compression. Dans le milieu interstellaire ou interplanétaire, les
particules sont diffusées par des distorsions magnétiques nommées ondes
d'Alfvén. Généralement, la vitesse de propagation de ces ondes est très
faible et elles sont assimilables à un phénomène stationnaire. Des
particules de haute énergie peuvent interagir et subir une diffusion isotrope.
Si un tel processus prend place au voisinage d'une onde de choc, il s'ensuivra
que les particules très énergétiques
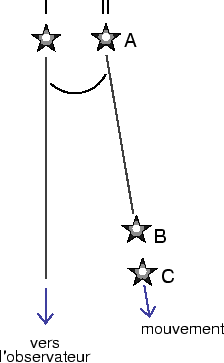
qui se meuvent avec le fluide vont croiser
le front d'onde un grand nombre de fois avant d'être transmises de l'autre
côté. A chaque fois qu'une particule franchit le front, elle subit un gain
Doppler d'énergie associé au changement de référentiel. Le
changement moyen d'énergie pour une particule relativiste est donné par
est le
rapport de compression. Dans le milieu interstellaire ou interplanétaire, les
particules sont diffusées par des distorsions magnétiques nommées ondes
d'Alfvén. Généralement, la vitesse de propagation de ces ondes est très
faible et elles sont assimilables à un phénomène stationnaire. Des
particules de haute énergie peuvent interagir et subir une diffusion isotrope.
Si un tel processus prend place au voisinage d'une onde de choc, il s'ensuivra
que les particules très énergétiques
qui se meuvent avec le fluide vont croiser
le front d'onde un grand nombre de fois avant d'être transmises de l'autre
côté. A chaque fois qu'une particule franchit le front, elle subit un gain
Doppler d'énergie associé au changement de référentiel. Le
changement moyen d'énergie pour une particule relativiste est donné par
![]() . Individuellement, les particules gagnent de
l'énergie à un taux exponentiel jusqu'à leur transmission définitive.
Cependant, à cause du mouvement aléatoire, le nombre de fois
que l'une d'elles traverse le front d'onde est variable et la probabilité de
s'échapper peut s'écrire
. Individuellement, les particules gagnent de
l'énergie à un taux exponentiel jusqu'à leur transmission définitive.
Cependant, à cause du mouvement aléatoire, le nombre de fois
que l'une d'elles traverse le front d'onde est variable et la probabilité de
s'échapper peut s'écrire ![]() . Après
. Après ![]() diffusions, la fraction de
particules présentes du côté en question est
diffusions, la fraction de
particules présentes du côté en question est ![]() . Les particules
vont donc gagner de l'énergie comme
. Les particules
vont donc gagner de l'énergie comme
![]() , où
, où
![]() est l'énergie initiale. La fraction de particules dont l'énergie
est supérieure à
est l'énergie initiale. La fraction de particules dont l'énergie
est supérieure à  varie donc comme
varie donc comme ![]() et la fonction de
distribution comme la dérivée, c'est-à-dire
et la fonction de
distribution comme la dérivée, c'est-à-dire
Ce mécanisme est supposé très efficace dans le flot supersonique qui
entoure un trou noir [26]. Il existe néanmoins une limite à
l'énergie à laquelle une particule relativiste peut être ainsi
accélérée [27]. La fréquence synchrotron maximale qu'il est
possible d'atteindre pour un électron subissant ce mécanisme est de
l'ordre de ![]() Hz. Mais l'effet Compton inverse, dont il sera davantage
question dans la dernière partie de ce mémoire, permet d'atteindre des
énergies bien plus élevées.
Hz. Mais l'effet Compton inverse, dont il sera davantage
question dans la dernière partie de ce mémoire, permet d'atteindre des
énergies bien plus élevées.
Un autre effet doit nécessairement être pris en compte. Il
résulte de l'existence d'ondes transverses se propageant dans un plasma le
long des lignes de champ magnétique. Ces ondes d'Alfvén sont
incompressibles et dominantes par rapport aux ondes magnéto-soniques se
propageant de façon compressible. Elles permettent le couplage des
rayons cosmiques avec le milieu en jouant le rôle de centres diffuseurs.
Le processus de Fermi du second ordre est une interaction résonnante des
particules avec les ondes d'Alfvén. Il est essentiel de noter que
contrairement à une idée reçue, ce mécanisme est aussi efficace que
le processus de Fermi du premier ordre [28]. L'interaction
résonnante prend naissance lorsque le rayon de Larmor d'une particule
chargée se trouve égal à la longueur d'onde de la perturbation
d'Alfvén. L'importance prépondérante de ce processus de Fermi du second
ordre vient de ce qu'il a nécessairement lieu en aval du choc et que sa
contribution ne peut donc pratiquement jamais être négligée. Il joue,
en quelque sorte, le rôle d'injecteur.
Il est intéressant de remarquer que ces processus comportent des bornes
énergétiques. L'énergie minimum nécessaire à leur fonctionnement
est:
Les processus de choc injectent dans le milieu des spectres voisins de ![]() .
Les calculs les plus récents, tenant compte de corrections de non-linéarité
initialement négligées dans l'équation de transport de Fokker-Planck,
conduisent à un léger durcissement en
.
Les calculs les plus récents, tenant compte de corrections de non-linéarité
initialement négligées dans l'équation de transport de Fokker-Planck,
conduisent à un léger durcissement en
![]() . Mais ce spectre est
ensuite dégradé par les nombreuses pertes radiatives (de toutes façons
indispensables pour éviter une divergence de l'énergie) qui laissent une grande
latitude d'indices spectraux, a priori observables.
. Mais ce spectre est
ensuite dégradé par les nombreuses pertes radiatives (de toutes façons
indispensables pour éviter une divergence de l'énergie) qui laissent une grande
latitude d'indices spectraux, a priori observables.