suivant: Les trous noirs primordiaux
monter: Comment traquer les trous
précédent: Gammas primaires
Table des matières
Les sections précédentes ont montré comment les antiprotons et les gammas
cosmiques permettaient d'obtenir des limites supérieures sur la densité de trous
noirs primordiaux dans l'Univers contemporain. Nous proposons ici d'aller plus
loin et de présenter un moyen envisageable pour procéder à une détection.
L'idée [40,31] consiste à utiliser cette fois des antideutérons,
noyaux légers formés d'un antiproton et d'un antineutron. Le rapport signal
bruit attendu devrait être largement supérieur pour des raisons essentiellement
cinématiques : le seuil de création des 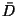 par interaction du rayonnement
cosmique sur la matière interestellaire
par interaction du rayonnement
cosmique sur la matière interestellaire
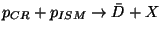 est
est
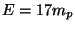 dans le
laboratoire, soit 2.4 fois plus élevé que pour la production d'antiprotons. Le centre de
masse de la réaction est donc en mouvement rapide et la probabilité de
production d'un antideutéron au voisinage du repos est faible. De plus, l'énergie
de liaison du noyau de deutérium est faible, ce qui rend invraisemblable les
phénomènes de perte d'énergie sans destruction (cet argument est sujet à
caution, il peut même sans doute être réfuté : M. Buenerd et K. Protassov, en préparation).
dans le
laboratoire, soit 2.4 fois plus élevé que pour la production d'antiprotons. Le centre de
masse de la réaction est donc en mouvement rapide et la probabilité de
production d'un antideutéron au voisinage du repos est faible. De plus, l'énergie
de liaison du noyau de deutérium est faible, ce qui rend invraisemblable les
phénomènes de perte d'énergie sans destruction (cet argument est sujet à
caution, il peut même sans doute être réfuté : M. Buenerd et K. Protassov, en préparation).
Pour évaluer la production d'antideutérons issus de l'évaporation de trous
noirs primordiaux, il faut implémenter un modèle de coalescence dans la
description du processus d'évaporation. Celui-ci rend compte de ce que si un
antiproton et un antineutron sont produits au même instant avec des impulsions
(vectorielles) suffisamment proches, ils peuvent donner naissance à un
antideutéron. Ce modèle a été développé dans le cadre de l'étude des
noyaux légers produits par interactions proton-noyau (voir [41] pour une
synthèse) et se fonde sur des considérations d'espace de phase:
où 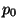 est l'impulsion de coalescence qui reste un paramètre
phénoménologique et
est l'impulsion de coalescence qui reste un paramètre
phénoménologique et 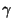 est le facteur de Lorentz. Dans le cas qui nous intéresse, ce modèle de
coalescence doit être implémenté directement dans l'étude de
l'évaporation quantique et nous utilisons la procédure suivante:
est le facteur de Lorentz. Dans le cas qui nous intéresse, ce modèle de
coalescence doit être implémenté directement dans l'étude de
l'évaporation quantique et nous utilisons la procédure suivante:
- dans chaque jet hadronique simulé, les antiprotons sont recherchés
- si un antiproton est trouvé, les antineutrons sont recherchés
- si un antineutron est trouvé, les impulsions sont comparées
- si la différence des impulsions est inférieure à l'impulsion de
coalescence
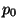 , un antideutéron est formé.
, un antideutéron est formé.
Il est important de prendre garde à ce que l'impulsion de coalescence n'est
pas invariante de Lorentz et à implémenter le test, non pas dans le
référentiel du laboratoire, mais dans le référentiel du centre de masse
du système antiproton-antineutron. On devrait en fait parler d'ellipsoïde de
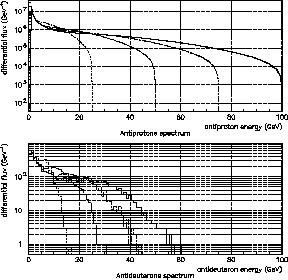
coalescence dans le référentiel du laboratoire. La figure 1.10
présente, à gauche, le spectre différentiel d'antiprotons résultant de
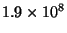 quarks
quarks 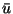 générés à 100, 65, 50, 25 GeV et la
distribution résultante d'antideutérons pour
générés à 100, 65, 50, 25 GeV et la
distribution résultante d'antideutérons pour 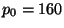 MeV. Le rapport entre
les flux d'antideutérons et d'antiprotons est de l'ordre de
MeV. Le rapport entre
les flux d'antideutérons et d'antiprotons est de l'ordre de 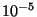 , ce qui
n'est pas surprenant puisqu'en accord avec les rapports de sections efficaces
mesurées (voir références dans [39]). Il existe néanmoins
une importante dispersion des valeurs mesurées et c'est la raison pour laquelle
nous n'avons pas fixé
, ce qui
n'est pas surprenant puisqu'en accord avec les rapports de sections efficaces
mesurées (voir références dans [39]). Il existe néanmoins
une importante dispersion des valeurs mesurées et c'est la raison pour laquelle
nous n'avons pas fixé 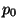 à une valeur donnée mais laissé ce
paramètre libre entre 60 MeV et 280 MeV.
à une valeur donnée mais laissé ce
paramètre libre entre 60 MeV et 280 MeV.
Figure:
Gauche : Flux d'antiprotons (haut) et d'antideutérons (bas) générés par des
quarks u à 25, 50, 75 et 100 GeV. Droite : Flux d'antideutérons secondaires (points) et venant de PBH
(trait) faisant apparaître une large fenêtre de détection à basse énergie.
|
|
Le flux d'antideutérons issus de trous noirs s'écrit donc:
où
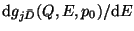 est la fonction de fragmentation
en antideutérons évaluée par implémentation du modèle de coalescence
dans la simulation PYTHIA (après transformation de Lorentz). Etant donné que
le nombre d'antideutérons produits est extrêmement faible, un certain nombre
d'interpolations ont dû être mises en
est la fonction de fragmentation
en antideutérons évaluée par implémentation du modèle de coalescence
dans la simulation PYTHIA (après transformation de Lorentz). Etant donné que
le nombre d'antideutérons produits est extrêmement faible, un certain nombre
d'interpolations ont dû être mises en  uvre de façon à éviter un
temps de calcul divergent. Il a été vérifié que leur influence est
négligeable. Le spectre d'antideutérons produit est alors convolué avec
le spectre de masse des PBH dans une approche similaire à celle employée
pour les antiprotons. Le modèle de diffusion ensuite utilisé est directement
dérivé de celui précédemment décrit. Le halo de matière noire est
décrit par les différentes distributions habituelles. La modulation solaire
est prise en compte avec un champ
uvre de façon à éviter un
temps de calcul divergent. Il a été vérifié que leur influence est
négligeable. Le spectre d'antideutérons produit est alors convolué avec
le spectre de masse des PBH dans une approche similaire à celle employée
pour les antiprotons. Le modèle de diffusion ensuite utilisé est directement
dérivé de celui précédemment décrit. Le halo de matière noire est
décrit par les différentes distributions habituelles. La modulation solaire
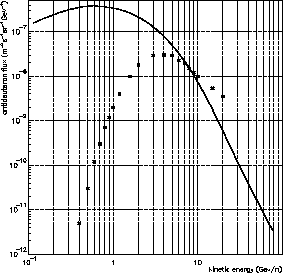
est prise en compte avec un champ 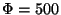 MV. La figure 1.10
présente, à doite, le flux d'antideutérons au niveau de l'atmosphère
pour une impulsion de coalescence
MV. La figure 1.10
présente, à doite, le flux d'antideutérons au niveau de l'atmosphère
pour une impulsion de coalescence 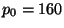 MeV, une taille de halo diffusif
MeV, une taille de halo diffusif
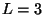 kpc et une densité locale de trous noirs
kpc et une densité locale de trous noirs
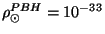 g
cm
g
cm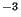 (autorisée par la limite supérieure donnée dans les deux
sections précédentes). Cette même figure présente également le fond
d'antideutérons secondaires calculé dans [31] et montre l'existence
d'une large fenêtre à basse énergie pour la détection.
(autorisée par la limite supérieure donnée dans les deux
sections précédentes). Cette même figure présente également le fond
d'antideutérons secondaires calculé dans [31] et montre l'existence
d'une large fenêtre à basse énergie pour la détection.
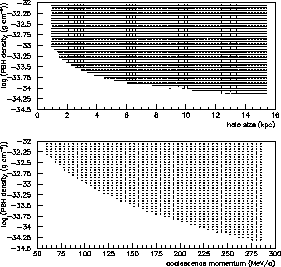
Figure:
Gauche : Espace des paramètres accessibles à
l'expérience AMS en 3 ans de
prise de données : l'épaisseur de halo diffusif varie de 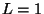 à
à
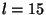 kpc, l'impulsion de coalescence varie de
kpc, l'impulsion de coalescence varie de 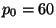 à
à 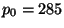 MeV/c et
la densité de PBH varie de
MeV/c et
la densité de PBH varie de
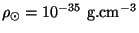 . Droite :
même chose pour l'exprérience GAPS.
. Droite :
même chose pour l'exprérience GAPS.
|
|
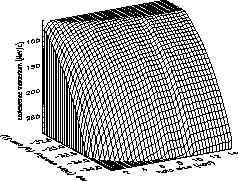
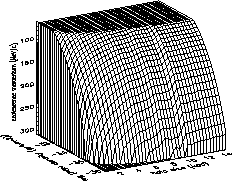
La figure 1.11 présente de façon globale
l'espace des paramètres (
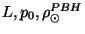 ) ainsi accessible aux futures expériences et la
figure 1.12 restreint ce dernier à 2 variables lorsque la troisième
est fixée à une valeur raisonnable. Il résulte de cette étude que le
détecteur AMS devrait améliorer la sensibilité actuelle d'un facteur 6
environ et le détecteur GAPS d'un facteur 40 environ. Il est, de plus, important
de noter que la situation est ici très différente de ce qu'elle était avec
les antiprotons : la limite n'est plus d'ordre physique mais d'ordre
instrumental. Alors que dans le premier cas le facteur limitant était le bruit
de fond de spallation, dans ce second cas le facteur limitant est la
sensibilité intégrée de l'instrument. C'est donc une nouvelle fenêtre
prometteuse qui est ouverte avec les antideutérons.
) ainsi accessible aux futures expériences et la
figure 1.12 restreint ce dernier à 2 variables lorsque la troisième
est fixée à une valeur raisonnable. Il résulte de cette étude que le
détecteur AMS devrait améliorer la sensibilité actuelle d'un facteur 6
environ et le détecteur GAPS d'un facteur 40 environ. Il est, de plus, important
de noter que la situation est ici très différente de ce qu'elle était avec
les antiprotons : la limite n'est plus d'ordre physique mais d'ordre
instrumental. Alors que dans le premier cas le facteur limitant était le bruit
de fond de spallation, dans ce second cas le facteur limitant est la
sensibilité intégrée de l'instrument. C'est donc une nouvelle fenêtre
prometteuse qui est ouverte avec les antideutérons.
Il faut néanmoins noter que la diffusion en énergie des 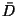 (i.e. les interactions inélastiques non-anihilantes) qui a
été ici supposée négligeable sur des arguments de fragilité du noyau
(l'énergie de liaison est très faible) pourrait être en fait nettement
plus importante si l'on se réfère au comportement inféré de celui des
protons [42]. De plus, des antideutérons pourraient être produits à
plus basse énergie par la réaction
(i.e. les interactions inélastiques non-anihilantes) qui a
été ici supposée négligeable sur des arguments de fragilité du noyau
(l'énergie de liaison est très faible) pourrait être en fait nettement
plus importante si l'on se réfère au comportement inféré de celui des
protons [42]. De plus, des antideutérons pourraient être produits à
plus basse énergie par la réaction
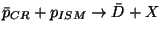 [43]. Le flux incident dans cette dernière approche est très
faible (puisque le rapport
[43]. Le flux incident dans cette dernière approche est très
faible (puisque le rapport 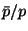 est de l'ordre de
est de l'ordre de
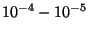 ) mais
le seuil étant plus bas, elle peut contribuer significativement à la partie
"sub-GeV" du spectre. Les études préliminaires sur ces deux points laissent
penser que la fenêtre de détection à basse énergie demeure mais que son
amplitude se trouve réduite à un ordre de grandeur environ.
) mais
le seuil étant plus bas, elle peut contribuer significativement à la partie
"sub-GeV" du spectre. Les études préliminaires sur ces deux points laissent
penser que la fenêtre de détection à basse énergie demeure mais que son
amplitude se trouve réduite à un ordre de grandeur environ.
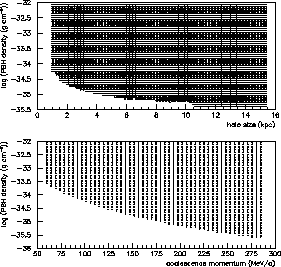
Figure:
Gauche : Espace des paramètres accessibles à
l'expérience AMS en 3 ans de
prises de données pour 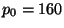 MeV/c (haut) et pour
MeV/c (haut) et pour 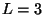 kpc (bas).
Droite : Même chose pour l'expérience GAPS.
kpc (bas).
Droite : Même chose pour l'expérience GAPS.
|
|




suivant: Les trous noirs primordiaux
monter: Comment traquer les trous
précédent: Gammas primaires
Table des matières
Aurelien Barrau
2004-07-01
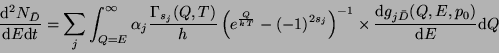
![]() ) ainsi accessible aux futures expériences et la
figure 1.12 restreint ce dernier à 2 variables lorsque la troisième
est fixée à une valeur raisonnable. Il résulte de cette étude que le
détecteur AMS devrait améliorer la sensibilité actuelle d'un facteur 6
environ et le détecteur GAPS d'un facteur 40 environ. Il est, de plus, important
de noter que la situation est ici très différente de ce qu'elle était avec
les antiprotons : la limite n'est plus d'ordre physique mais d'ordre
instrumental. Alors que dans le premier cas le facteur limitant était le bruit
de fond de spallation, dans ce second cas le facteur limitant est la
sensibilité intégrée de l'instrument. C'est donc une nouvelle fenêtre
prometteuse qui est ouverte avec les antideutérons.
) ainsi accessible aux futures expériences et la
figure 1.12 restreint ce dernier à 2 variables lorsque la troisième
est fixée à une valeur raisonnable. Il résulte de cette étude que le
détecteur AMS devrait améliorer la sensibilité actuelle d'un facteur 6
environ et le détecteur GAPS d'un facteur 40 environ. Il est, de plus, important
de noter que la situation est ici très différente de ce qu'elle était avec
les antiprotons : la limite n'est plus d'ordre physique mais d'ordre
instrumental. Alors que dans le premier cas le facteur limitant était le bruit
de fond de spallation, dans ce second cas le facteur limitant est la
sensibilité intégrée de l'instrument. C'est donc une nouvelle fenêtre
prometteuse qui est ouverte avec les antideutérons.
![]() (i.e. les interactions inélastiques non-anihilantes) qui a
été ici supposée négligeable sur des arguments de fragilité du noyau
(l'énergie de liaison est très faible) pourrait être en fait nettement
plus importante si l'on se réfère au comportement inféré de celui des
protons [42]. De plus, des antideutérons pourraient être produits à
plus basse énergie par la réaction
(i.e. les interactions inélastiques non-anihilantes) qui a
été ici supposée négligeable sur des arguments de fragilité du noyau
(l'énergie de liaison est très faible) pourrait être en fait nettement
plus importante si l'on se réfère au comportement inféré de celui des
protons [42]. De plus, des antideutérons pourraient être produits à
plus basse énergie par la réaction
![]() [43]. Le flux incident dans cette dernière approche est très
faible (puisque le rapport
[43]. Le flux incident dans cette dernière approche est très
faible (puisque le rapport ![]() est de l'ordre de
est de l'ordre de
![]() ) mais
le seuil étant plus bas, elle peut contribuer significativement à la partie
"sub-GeV" du spectre. Les études préliminaires sur ces deux points laissent
penser que la fenêtre de détection à basse énergie demeure mais que son
amplitude se trouve réduite à un ordre de grandeur environ.
) mais
le seuil étant plus bas, elle peut contribuer significativement à la partie
"sub-GeV" du spectre. Les études préliminaires sur ces deux points laissent
penser que la fenêtre de détection à basse énergie demeure mais que son
amplitude se trouve réduite à un ordre de grandeur environ.