



Next: Cascade initiée par un
Up: Images Tcherenkov et paramètres
Previous: Images Tcherenkov et paramètres
Contents
Lorsqu'une particule chargée traverse un milieu transparent diélectrique avec
une vitesse proche de celle de la lumière (plus exactement supérieure à 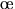 où
où 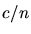 est l'indice de réfraction local), les atomes au voisinage de la
trajectoire sont distordus. Cet effet se manifeste dans les couches
électroniques et induit l'apparition effective de petits dipôles. Pour une
particule très rapide, le champ de polarisation est dissymétrique et provoque
l'apparition d'une émission radiative tout au long de la trajectoire. Lorsque la
condition
est l'indice de réfraction local), les atomes au voisinage de la
trajectoire sont distordus. Cet effet se manifeste dans les couches
électroniques et induit l'apparition effective de petits dipôles. Pour une
particule très rapide, le champ de polarisation est dissymétrique et provoque
l'apparition d'une émission radiative tout au long de la trajectoire. Lorsque la
condition 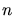 (avec
(avec 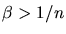 ) est
vérifiée, les interférences peuvent devenir constructives et un front d'onde
cohérent se forme à un angle d'émission
) est
vérifiée, les interférences peuvent devenir constructives et un front d'onde
cohérent se forme à un angle d'émission 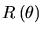 défini par:
défini par:
L'angle maximum d'émission pour des particules ultra-relativistes est ainsi
donné par
Pour un milieu homogène et isotrope, l'émission présente une symétrie
axiale et les radiations se répartissent sur une surface conique de demi-angle
au sommet 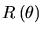 .
.
Le taux de production de radiation  par unité de longueur
par unité de longueur 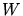 s'écrit
[55]:
s'écrit
[55]:
où 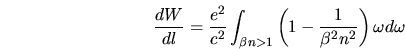 est la charge de l'électron et
est la charge de l'électron et 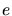 la pulsation. La distribution
spectrale résultante est typiquement maximale entre le bleu et l'UV. On peut
montrer par un traitement quantique détaillé [56] [57] que
l'énergie perdue par la particule suite à l' effet Tcherenkov est tout à fait
négligeable devant l'énergie perdue par ionisation ou par effet
bremsstrahlung.
la pulsation. La distribution
spectrale résultante est typiquement maximale entre le bleu et l'UV. On peut
montrer par un traitement quantique détaillé [56] [57] que
l'énergie perdue par la particule suite à l' effet Tcherenkov est tout à fait
négligeable devant l'énergie perdue par ionisation ou par effet
bremsstrahlung.
Blackett [58] a été le premier à suggérer que les rayons cosmiques
très énergétiques pourraient produire une certaine quantité de rayonnement
Tcherenkov en pénétrant dans l'atmosphère terrestre. Jelley [59] a
montré qu'au premier ordre les angles maxima et les énergies minima
pouvaient s'écrire
où 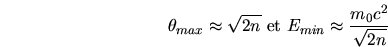 est la masse au repos de la particule. Il apparaît ainsi que le
seuil croît et que l'angle d'émission décroit avec l'altitude. Au niveau de la
mer, on obtient les énergies de seuil suivantes (table 6.1):
est la masse au repos de la particule. Il apparaît ainsi que le
seuil croît et que l'angle d'émission décroit avec l'altitude. Au niveau de la
mer, on obtient les énergies de seuil suivantes (table 6.1):
Table 6.1:
Seuil de production de lumière Tcherenkov au niveau de la mer.
| Particule |
Seuil |
|
|---|
| électrons |
21 MeV |
|
| muons |
4.4 GeV |
|
| protons |
39 GeV |
|
|
Aux énergies qui nous intéressent, la contribution principale à la
lumière Tcherenkov d'une
cascade cosmique dans l'atmosphère provient des électrons. L'angle
d'émission est de l'ordre de 1.3 degré au niveau de la mer.
Pour une bande de longueurs d'onde comprises entre 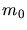 et
et 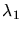 , le
taux de production de photons Tcherenkov maximum dans une atmosphère
dont l'indice de réfraction varie exponentiellement
(
, le
taux de production de photons Tcherenkov maximum dans une atmosphère
dont l'indice de réfraction varie exponentiellement
(
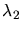 )
est donné par:
)
est donné par:
où 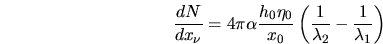 est la profondeur atmosphérique à une hauteur
est la profondeur atmosphérique à une hauteur 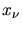 ,
, 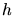 la
profondeur atmosphérique au niveau de la mer (
la
profondeur atmosphérique au niveau de la mer (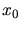 kg.m
kg.m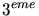 ),
), 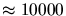 la hauteur d'échelle (=
la hauteur d'échelle (=
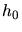 km) et
km) et 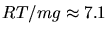 l'indice de réfraction en excès
par rapport à 1 au niveau de la mer (
l'indice de réfraction en excès
par rapport à 1 au niveau de la mer (
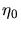 ). Cela conduit
à un taux de l'ordre de 34 photons.kg
). Cela conduit
à un taux de l'ordre de 34 photons.kg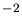 .m
.m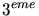 entre 300 et 660 nm.
entre 300 et 660 nm.
L'absorption, la diffraction et la diffusion dans l'atmosphère modifient les
caractéristiques de l'émission Tcherenkov mais l'effet dominant est de loin la
diffusion Coulombienne multiple des électrons. Les angles en question sont de
l'ordre de (ou supérieurs) ceux de l'émission Tcherenkov. Rossi et Greisen
[60] ont montré que:
où 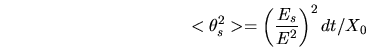 est l'angle de diffusion carré moyen,
est l'angle de diffusion carré moyen, 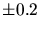 l'énergie de la
particule,
l'énergie de la
particule, 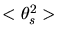 une constante (
une constante (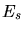 MeV) et
MeV) et 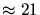 la longueur de la
trajectoire. Pour un électron typique de 100 MeV ayant parcouru une longueur de
radiation
la longueur de la
trajectoire. Pour un électron typique de 100 MeV ayant parcouru une longueur de
radiation 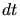 dans l'air (
dans l'air (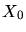 g.cm
g.cm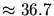 ), l'angle de diffusion moyen
est d'environ 12 degrés, un ordre de grandeur plus grand que l'angle
d'émission Tcherenkov. Il apparaît ainsi que la diffusion Coulombienne
domine presque toujours l'émission Tcherenkov dans la détermination de la
distribution angulaire de la lumière de la cascade. C'est le point clef pour
comprendre la forme des images décrite ultérieurement.
), l'angle de diffusion moyen
est d'environ 12 degrés, un ordre de grandeur plus grand que l'angle
d'émission Tcherenkov. Il apparaît ainsi que la diffusion Coulombienne
domine presque toujours l'émission Tcherenkov dans la détermination de la
distribution angulaire de la lumière de la cascade. C'est le point clef pour
comprendre la forme des images décrite ultérieurement.
Le rayon Tcherenkov d'une cascade atmosphérique pour une particule se
déplaçant verticalement à une hauteur 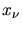 est donné par:
est donné par:
Pour  , on obtient un rayon
, on obtient un rayon 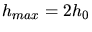 m.
m.




Next: Cascade initiée par un
Up: Images Tcherenkov et paramètres
Previous: Images Tcherenkov et paramètres
Contents
Aurelien Barrau
2004-07-01
![]() où
où ![]() est l'indice de réfraction local), les atomes au voisinage de la
trajectoire sont distordus. Cet effet se manifeste dans les couches
électroniques et induit l'apparition effective de petits dipôles. Pour une
particule très rapide, le champ de polarisation est dissymétrique et provoque
l'apparition d'une émission radiative tout au long de la trajectoire. Lorsque la
condition
est l'indice de réfraction local), les atomes au voisinage de la
trajectoire sont distordus. Cet effet se manifeste dans les couches
électroniques et induit l'apparition effective de petits dipôles. Pour une
particule très rapide, le champ de polarisation est dissymétrique et provoque
l'apparition d'une émission radiative tout au long de la trajectoire. Lorsque la
condition ![]() (avec
(avec ![]() ) est
vérifiée, les interférences peuvent devenir constructives et un front d'onde
cohérent se forme à un angle d'émission
) est
vérifiée, les interférences peuvent devenir constructives et un front d'onde
cohérent se forme à un angle d'émission ![]() défini par:
défini par:
![]() par unité de longueur
par unité de longueur ![]() s'écrit
[55]:
s'écrit
[55]:
![]() et
et ![]() , le
taux de production de photons Tcherenkov maximum dans une atmosphère
dont l'indice de réfraction varie exponentiellement
(
, le
taux de production de photons Tcherenkov maximum dans une atmosphère
dont l'indice de réfraction varie exponentiellement
(
![]() )
est donné par:
)
est donné par:
![]() est donné par:
est donné par: