



Next: Contributions des électrons du
Up: Calcul des paramètres physiques
Previous: Caractéristiques du jet d'électrons
Contents
Soient 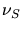 et
et 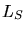 les luminosités synchrotron et Compton. Dans le modèle SSC,
leur rapport est égal au rapport
des densités d'énergie magnétique et de radiation,
à partir desquels on peut déduire le rayon de la zone d'émission:
les luminosités synchrotron et Compton. Dans le modèle SSC,
leur rapport est égal au rapport
des densités d'énergie magnétique et de radiation,
à partir desquels on peut déduire le rayon de la zone d'émission:
Il n'y a pas d'équivalent pour le modèle EC car on ne dispose pas
d'informations sur la densité d'énergie externe.
Cependant on peut avoir accès à la taille maximale de la région d'émission
en utilisant la durée minimale des émissions gamma détectées. Cette contrainte
est pertinente uniquement si le modèle EC correspond à un bref sursaut,
et non à l'état haut. On pose 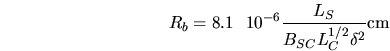 le temps caractéristique du sursaut (en heures).
On dérive alors:
le temps caractéristique du sursaut (en heures).
On dérive alors:
où 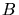 est la fraction du temps caractéristique du sursaut pendant laquelle chaque élément
se trouve atteint par la perturbation et
est la fraction du temps caractéristique du sursaut pendant laquelle chaque élément
se trouve atteint par la perturbation et
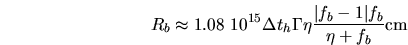 .
.
La durée du sursaut peut également être utilisée pour déterminer
la densité énergétique de la source diffuse.
Soient 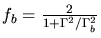 la luminosité de la source centrale (supposée
dominée par la bosse UV) et
la luminosité de la source centrale (supposée
dominée par la bosse UV) et 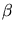 la fraction de la luminosité centrale
contribuant à la radiation diffuse pour une distance au centre de
la fraction de la luminosité centrale
contribuant à la radiation diffuse pour une distance au centre de 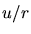 . Dans le cas
d'une diffusion électronique,
. Dans le cas
d'une diffusion électronique, 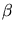 est en première approximation
égal à l'épaisseur optique de Thomson
le long de
est en première approximation
égal à l'épaisseur optique de Thomson
le long de 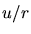 ; dans le cas d'un retraitement des photons avec ré-émission en raies,
; dans le cas d'un retraitement des photons avec ré-émission en raies,
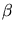 représente la fraction de couverture des nuages multipliée par un coefficient d'efficacité.
On peut alors écrire:
représente la fraction de couverture des nuages multipliée par un coefficient d'efficacité.
On peut alors écrire:




Next: Contributions des électrons du
Up: Calcul des paramètres physiques
Previous: Caractéristiques du jet d'électrons
Contents
Aurelien Barrau
2004-07-01
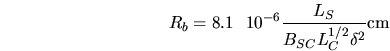 le temps caractéristique du sursaut (en heures).
On dérive alors:
le temps caractéristique du sursaut (en heures).
On dérive alors: