



Next: La taille de la
Up: Calcul des paramètres physiques
Previous: Description du spectre et
Contents
On peut, dans un premier temps, supposer un jet chaud et négliger
les effets de Klein-Nishina.
L'angle de vue par rapport à l'axe du jet est noté 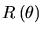 .
.
 représente le facteur Doppler produit par le mouvement relativiste du nodule
dans le plasma émetteur. Il vaut
représente le facteur Doppler produit par le mouvement relativiste du nodule
dans le plasma émetteur. Il vaut
Dans les équations suivantes, l'indice 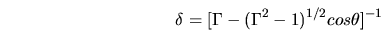 est relatif à l'émission synchrotron,
est relatif à l'émission synchrotron,
 aux photons externes,
aux photons externes, 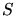 au
Compton-inverse sur les photons synchrotron (hypothèse SSC) et
au
Compton-inverse sur les photons synchrotron (hypothèse SSC) et
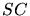 au Compton-inverse sur les photons externes
(hypothèse EC); les fréquences sont celles des maxima des plateaux de la distribution
spectrale d'énergie.
On a alors:
au Compton-inverse sur les photons externes
(hypothèse EC); les fréquences sont celles des maxima des plateaux de la distribution
spectrale d'énergie.
On a alors:
et
Si
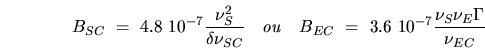 est plus grand que
est plus grand que 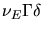 , pour un même spectre observé,
le modèle SSC implique une plus grande énergie des électrons et une plus faible
valeur de l'intensité du champ magnétique que le modèle EC.
, pour un même spectre observé,
le modèle SSC implique une plus grande énergie des électrons et une plus faible
valeur de l'intensité du champ magnétique que le modèle EC.




Next: La taille de la
Up: Calcul des paramètres physiques
Previous: Description du spectre et
Contents
Aurelien Barrau
2004-07-01
![]() .
.
![]() représente le facteur Doppler produit par le mouvement relativiste du nodule
dans le plasma émetteur. Il vaut
représente le facteur Doppler produit par le mouvement relativiste du nodule
dans le plasma émetteur. Il vaut
![\begin{displaymath}
\delta = [\Gamma - (\Gamma^2 -1 )^{1/2} cos \theta]^{-1}
\end{displaymath}](img814.png)