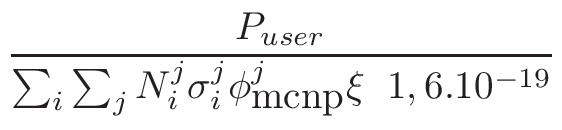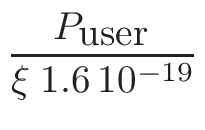Previous: "Class_Summary"
Report: LPSC 0912
Report: IPNO-09-01
MURE,
MCNP Utility for Reactor Evolution
User Guide - Version 1.9
November 2014
Main Contributors :
-
-
• O. Méplan (alias PTO), LPSC Grenoble
-
-
• J. Wilson (alias JW), IPN Orsay
-
-
• A. Bidaud (alias le bid), LPSC Grenoble
-
-
• S. David (alias GTS), IPN Orsay
-
-
• N. Capellan (alias Nico la Star), LPSC Grenoble
-
-
• B. Leniau (alias BLG), IPN Orsay
-
-
• A. Nuttin (alias Nut), LPSC Grenoble
-
-
• Frantisek Havluj, UJV, Czech Republic
-
-
• Radim Vocka, UJV, Czech Republic
-
-
• and in the past:
-
-
• R. Chambon (alias Le caribou), LPSC, Grenoble, now back to Canada
-
-
• F. Michel-Sendis (alias FMS), IPN Orsay, Now @CEA
-
-
• F. Perdu (alias WEC), LPSC, Grenoble, Now @CEA
-
-
• L. Perrot, IPN Orsay
See also the FAQ
The main aim of the MURE[1,2]package is to perform nuclear reactor time-evolution using the widely-used
particle transport code MCNP[3](a Monte
Carlo code which is mostly written in FORTRAN). Many depletion codes
exist for determining time-dependent fuel composition and reaction
rates. These codes are either based on solving Boltzman equation using
deterministic methods or based on Monte-Carlo method for neutron transport.
Among them, one has to cite MCNPX/CINDER 90[4], MONTEBURN[5],
KENO/ORIGEN[6], MOCUP[7], MCB[8], VESTA/MORET[14,15],
TRIPOLI-4D[16]... which provide neutron transport and depletion
capabilities. However, the way to control (or interact with) the evolution
are either limited to specific procedure and/or difficult to implement.
In MURE, due to the Object-oriented programming, any user can
define his own way to interact with evolution. It is also good to
have lots of M-C evolution codes to compare and benchmark them to
understand physics approximations of each ones. Moreover, MURE
provides a simple graphical interface to visualize the results. It
also provides a way to couple the neutronics (with or without fuel
burn-up) and thermal-hydraulics using either an open source simple
code developed in MURE (BATH, Basic Approach of Thermal
Hydraulics) or a sub-channel 3D code, COBRA-EN[10,11].
But MURE can also be used just as an interface to MCNP
to build geometries (e.g. for neutronics experiments simulation).
MURE is based on C++ objects allowing a great flexibility
in the use1.1. There are 3 main parts in this library:
-
-
• Definition of the geometry, materials, neutron source, tallies, ...
-
-
• Construction of the nuclear tree, the network of links between neighbouring
nuclei via radioactive decays and nuclear reactions.
-
-
• Evolution of some materials, by solving the corresponding Bateman's
equations.
-
-
• Thermal-hydraulics: it couples neutronics, thermal-hydraulics and,
if needed, fuel evolution.
-
-
• Part 1 can be used independently of the 2 others; it allows ``easy''
generation of MCNP input files by providing a set of classes
for describing complex geometries. The ability to make quick global
changes to reactor component dimensions and the ability to create
large lattices of similar components are two important features that
can be implemented by the C++ interface. It should be noted that some
knowledge of MCNP is very useful in understanding the geometry
generation philosophy.
-
-
• Part 2 builds the specific nuclear tree from an initial material composition
(list of nuclei). The tree of each ``evolving''1.2 nucleus is created by following the links between neighbours via
radioactive decay and/or reactions until a self-consistent set of
linked nuclei is extracted. Nuclei with half-lives very much shorter
than the evolution time steps, could be removed from the tree; mothers
and daughters of these removed nuclei are re-linked in the correct
way. Part 2 can also be used independently of the other two parts
to process cross-sections for MCNP at the desired temperature.
-
-
• Part 3 simulates the evolution of the fuel within a given reactor
over a time period of up to several years, by successive steps of
MCNP calculation and numerical integration of Bateman's equations.
Each time MCNP is called, the reactor fuel composition will
change due to the fission/capture/decay process occurring inside.
Changes in geometry, temperature, external feeding or extraction during
the evolution can also be taken into account. Obviously this part
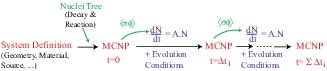
is not independent of the 2 others1.3 (see figure 1.1).
Figure 1.1:
Principle of fuel evolution in MURE.
 |
-
-
• Part 4 consists of coupling the Oak Ridge National Laboratory code
COBRA-EN (COolant Boiling in Rod
Arrays) with MURE. COBRA is a sub-channel
code that allows steady-state and transient analysis of the coolant
in rod arrays. The simulation of flow is based on a three or four
partial differential equations : conservation of mass, energy and
momentum vector for the water liquid/vapor mixture (optionally a fourth
equation can be added which tracks the vapor mass separately). The
heat transfer model is featured by a full boiling curve, comprising
the basic heat transfer regimes : single phase forced convection,
sub-cooled nucleate boiling, saturated nucleate boiling, transition
and film boiling. Heat conduction in the fuel and the cladding is
calculated using the balance equation.
The use of this package requires the following installation:
-
-
• a C++ compiler (mandatory). MURE is developed using gcc
(all version between 2.96 and 4.7 are known to work perfectly).
-
-
• MCNP or MCNPX (mandatory, available at the NEA
DataBank & RSICC).
-
-
• Nuclear data files process for MCNP (ACE format) and/or
NJOY to process ENDF files into the ACE format (Nuclear
data in ACE format are mandatory).
-
-
• COBRA-EN for the thermal-hydraulic part (available the atNEA
DataBank & RSICC)
-
-
• The ROOT graphical tools developed at CERN (http://root.cern.ch)
is necessary if user wants to use the post treatment GUI tools. In
the GUI, radiotoxicity of fuel/waste can be calculated and plotted
if the LAPACK library is installed (Linear Algebra PACKage,
see http://www.netlib.org/lapack/index.html
or standard LINUX repositories (Redhat, Fedora, Ubuntu, ...) for pre-installed
versions)
At present, MURE has only been compiled and tested on LINUX/UNIX
platforms.
-
-
• Uncompress the archive file where you want to install MURE source.
-
- tar zxvf MURE_XX.tgz
or
-
- gunzip MURE_XX.tgz ; tar xvf MURE_XX.tar
This will create the ``data'', ``documentation'',
``examples'', ``gui'', ``lib'', ``source''
and ``utils'' directories in the MURE directory.
-
-
• Configure and Compile MURE
-
-
• A bash script is given in the MURE directory
-
- ./install.sh -h : full flag option
-
-
• main options are
-
-
• -MCNP-version=Num where Num is the
MCNP version (or its ACE data format) ; Num can be
either 4 (for MCNP 4 (MCNPX <2.5) compiled with 32 bit data) or 5
(for MCNP ≥5 (or MCNPX ≥2.5) compiled with 64 bit data.
MCNP Version 5 is the default.
-
-
• -ENSDF-path=path where path is a
valid directory path (absolute or relatif) to ENSDF main
directory files ; these optional data can be obtained at http://ie.lbl.gov/databases/ensdfserve.html,
download the "Complete ENSDF database"
and unzip it in /path_to_ENSDF_data/ENSDF.
-
-
• Quick install (with the default MCNP 5 version for binary ACE data
format 64 bits)
-
- ./install.sh
This script will create a config directory that contains
Makefile.config and config.hxx necessary
for all Makefiles and MureHeader.hxx respectively. Then,
it compiles ``external'' libraries (ValErr and mctal)
and the MUREpkg library and put them in ``MURE/lib''.
These libraries are shared libraries.
-
-
• Set the LD_LIBRARY_PATH (or SHLIB_PATH on HP-UX or LIBPATH on AIX)
in tcsh/csh
-
- setenv LD_LIBRARY_PATH "${LD_LIBRARY_PATH}:/path_to_MURE/MURE/lib"
or in bash/sh
-
- export LD_LIBRARY_PATH="${LD_LIBRARY_PATH}:/path_to_MURE/MURE/lib"
In MURE, the access to ACE MCNP cross-sections is done
for different purposes (find if cross-sections exist, find the total
cross-sections in order to write in MCNP input file only ``significant
nucleus'' (see 4.1.6), use of ``multi-group
flux'' evolution method (see item 5
of section 6.3), ...). The use of binary
ACE files improves the reading time (and also the disk space necessary
to store the cross-sections). In C/C++, reading/writing in unformatted
files (binary) is done by reading records of 1 byte long. But some
FORTRAN compilers such as IFORT of Intel read/write in unformatted
file with 4 bytes records. Thus if you want to use such a compiler
for MCNP/makxsf you have to force the record length in unformatted
files to be 1 byte. In the Intel IFORT compiler this is done
via the -assume byterecl flag of ifort command line
(see the System.gcf file of the config dir of MCNP distribution
where System is either Linux, AIX, ...).
In this section, it is explained how to build the 2 necessary files
BaseSummary.dat and AvailableReactionChart.dat (these
files are not provided in the districution). One supposes that a user
has a standard MCNP5 ENDF B6 base provided with MCNP5 and that
the user converts the ASCII version into a binary one with the ``makxsf''
of MCNP. The result of this will be a xsdir file and the nuclear data
in binary located in /path_2_ace_files directory (Verify
that in the xsdir the absolute path to data files is present).
-
-
• Then go to MURE/utils/datadir.
-
-
• Compile the ExtractXsdir.cxx file (compilation line is at
the end of the file).
-
-
• Then run it with ``ExtractXsdir''
-
-
• Answer ENDFB to the first question
-
-
• 6.8 to the second one
-
-
• /path_2_ace_files/xsdir to the third one
-
-
• and STD to the last one.
-
-
• After a while the BaseSummary.dat is created and contains
the following
-
- 1 1 0 ENDFB 6.1 293.62 .24c STD 1001.24c 0.999170 /path_2_ace_files/la150n2 0 2 1 10106 4096 512 2.5301E-08
...
1 1 0 ENDFB 6.1 293.62 .66c STD 1001.66c 0.999170 /path_2_ace_files/endf66a2 0 2 1 10128 4096 512 2.5301E-08
...
92 235 0 ENDFB 6.1 293.62 .66c STD 92235.66c 233.025000 /path_2_ace_files/endf66c2 0 2 6899 722105 4096 512 2.5301E-08 ptable
...
-
-
• Then compile (compilation line at the end of the file) and run CheckReaction
-
-
• copy AvailableReactionChart.dat and BaseSummary.dat
in MURE/data
-
-
• Now you can run any examples of MURE.
The directory MURE/examples contains commented examples on
howto use MURE. A README file suggests an order to
execute examples. For each example, a compilation
line is put at the end of the file. Here, 2 examples are described ;
other examples are described in this User Guide (see for example,
§ 3.8.1, 3.8.2, 3.8.3
and 3.5).
In this directory, one finds static examples (i.e. without burn-up
calculations) and their outputs1.4 (in MURE/examples/Output/ directory). To run some of these
examples you must provide an MCNP xsdir file, whereas
for other ones user has to build the BaseSummary.dat and
AvailableReactionChart.dat files. The ``evolution'' examples
are in MURE/examples/Evolution/ directory. Again you will find
an ``Output'' directory that contains directory output of the examples
(also gzip). In these result directories, one has suppressed the MCNP
``o'' and ``m'' files but left the MCNP input files as
well as the MURE results files.
This example (MURE/examples/Putin_example.cxx) shows basic
geometrical methods.
-
-
• One first builds 2 Materials (Graphite & Fuel).
-
-
• Then one defines the Shapes: they are just geometrical shapes
; in the example, one uses only Sphere.
-
-
• The ``put in'' operator is used to put 3 spheres like Russian dolls:
Smallest and Small are called Inside Shapes
of Medium.
-
-
• Then, this Medium ``matrioshka'' is duplicated with the Shape::Clone()
method: the Medium2 clone is an exact copy of Medium:
it contains a small sphere which contains a smaller one.
-
-
• Medium and Medium2 shapes are then translated (with
their inside shapes) and then put in the Big sphere.
-
-
• Then, Cells are built (MCNP cells): it associates
a Shape with a Material. The exterior (outBig
cell) is void and one has to specify a zero neutron importance because
neutrons will not be followed (default importance is 1). One has to
build all Cells for all Shapes:
-
-
• for Medium, Small and Smallest shapes, it is
easy because they have been explicitly declared
-
-
• Medium2 being a clone of Medium, it has also 2 inside
shapes: thus one has to define cells for these inside shapes: one
access to Shape::GetOriginalInsideShape() ;
by convention, the most inner inside shape has the index 0, then the
next one has the index 1, and so on.
-
-
• And finally, the MCNP file is built ; default name is ``inp''.
The aim of this example1.5 of evolution (MURE/examples/Evolution/EvolvingSphere.cxx)
is to show basic burn-up calculation in MURE. The example describes
a 50cm radius sphere with a inner sphere (R=30cm) of metal uranium,
a middle ring (thickness=10cm) of UOx fuel and an external water reflector
(thickness=10cm). The water will not evolve with time ; the thermal
power of this ``reactor'' is 100 MW and it is kept constant for
the whole evolution performed from t = 0 to t = 3 years.
-
-
• The file begins with some general MURE settings: DATADIR, Temperature
precision, Fission Product selection, ...
-
-
• Then 3 Materials are built: the water will not evolve whereas
the metal and oxide uranium are evolving Materials.
-
-
• Then Shapes are defined (the 3 spheres and the exterior of
the ``reactor'').
-
-
• The Cell part associates Shapes and Materials.
-
-
• Then one defines an isotropic, mono-energetic neutron source to run
in critical mode (KCODE).
-
-
• The directory for the evolution is set (where MCNP files and
evolution results will be written). The ``r'' files of MCNP
will be removed (they are in general not useful and very large).
-
-
• One important function concerning reactor evolution is to be called
here : it is the thermal power at which evolution is to be simulated.
This value is set using the gMURE->SetPower() where
the argument must be in watts. (c.f. Steady-state Power Normalization
in § D.1).
NOTE: For other applications
or if the user already knows which neutron flux he wants to simulate,
no power needs to be entered here but a tally normalization factor
must then be specified. This Tally Normalization
Factor can be set directly through the gMURE->SetTallyNormalizationFactor()method.
-
-
• Then one defines the 12-1=11 time steps at which a MCNP run
is done, in a vector. The first MCNP step is indeed at time
t=0 and is not defined in the vector. The evolution is performed up
to the end but the last MCNP run is just the antepenultimate
time step. This is important to know because this means the last values
for keff, fluxes, cross-sections are not MCNP values:
for keff the last value considered is the antepenultimate one.
The distribution package contains:
-
-
• The PDF version
of this user guide.
-
-
• A complete useful description of each
class
(headers)
The general structure of main MURE's classes is shown in figure 1.2.
Figure 1.2:
Main class structure of MURE. Main attributes are shown in
blue. A Shape_ptr is only a typedef of Reference_ptr for a Shape.
Idem for Nucleus_ptr.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[scale=0.8]{fig/classe}
\par
\end{centering}\par
\protect
\end{figure}](Timg2.gif) |
As it can be seen in figure 1.2, the link between
classes is assured by the main class MURE.
The MURE
class is some kind of super class that handles connections between
all the other classes. It controls all flows: MCNP file writing, volume
calculation (when needed), nuclei trees building, evolution, ...
A global pointer (gMURE) on this class is defined to allow
interaction between classes. For example, when the geometry has been
defined, as well as the MCNP source, Tallies, ...., the MCNP file
will be written using
-
- gMURE->BuildMCNPFile("myfile");
this will generate an MCNP input file called ``myfile''
(if no argument is given to the previous method, the default input
file name is ``inp'').
The name of MCNP exec command is given by
-
- gMURE->SetMCNPExec("mcnp");
the default value for the MCNP executable is ``mcnp4c''.
This name is important for evolution as well as for stochastic volume
calculation.
You can specify the particle running mode by either gMURE->SetModeN()
(the default) to run MCNP with neutron transport, gMURE->SetModeNP()
to transport neutrons and photons and so on.
Many methods are in-line defined, therefore examination of MURE
class header is strongly recommended (see Doxygen
class description ).
Different files are used or built in MURE. It is important
to know what these files are to understand the behavior of MURE.
This directory contains the most updated user guide and class documentations.
-
-
• the ``MURE/documentation/pdf'' directory contains the PDF
files
-
-
• the ``MURE/documentation/html'' directory contains the HTML
files, in particular an HTML version of the user guide (which is a
translation of the PDF one). HTML links are easier to use as well
as copy/paste for examples. Moreover the ``MURE/documentation/html/doxygen''
directory contains the automatic Doxygen description of classes.
Files in ``MURE/data''
In the root MURE tree, there is a very important directory
called ``data'' (known in MURE
as the DATADIR) ; this directory can be changed by using either
the environment variable DATADIR, or using the MURE::SetDATADIR()
method1.6. In this directory, you will find:
-
-
• chart.JEF3T: this file contains, for each nucleus, the half-life
time and the decay modes. It is a ``hand-made'' file from nuclear
data book and JEFF 3.0 library, from "Nuclides
and Isotopes", [12] and "Table
of Isotopes", [13].
-
-
• Mass.dat and NaturalIsotopeMass.dat contain respectively
the atomic mass for all nuclei and some natural compositions.
-
-
• FPavailable.dat and FPyield.bin are fission product
yield files: the first one is an ASCII file containing the Z,A of
fissiles, and the address of the fission yield (for the available
energies) in the binary FPyield.bin file. These files are built
from ENDF/B6 file. Source programs that build these files are in MURE/utils/fp.
These files are part of the MURE package and have been built for 32
and 64 bits computers ; if you want to use other FP yield, you need
to rebuild these files using MURE/utils/fp/GenerateFPYield.cxx
(the compilation line is at the end of the file).
-
-
• xsdirprequ.dat is the ``header'' of a general xsdir
(from the top to the ``directory'' keyword). It is used in
the automatic XSDIR construction.
-
-
• BaseSummary.dat is the file that contains all available nuclei,
their temperature and the corresponding xsdir line.
It is build from MURE/utils/datadir/ExtractTree.cxx and/or
MURE/utils/datadir/ExtractXsdir.cxx. The first one extracts
information from a directory tree and the second from an existing
xsdir. This file is the only way for MURE to use automatic
MCNP nucleus code.
-
-
• AvailableReactionChart.dat contains, for all nuclei of the
chart.JEF3T and BaseSummary.dat, whether or not
reactions are available for MCNP. The aim of this file is to speed
up the NucleiTree construction. It is built from MURE/utils/datadir/CheckReaction.cxx.
-
-
• IsomerProduction.dat contains necessary information to allow
the
(n, γ) isomer productions for some important nuclei such
as 241Am, 109Ag, ...
NOTE: When you add new nucleus or temperature
in nuclear cross-sections files, these modifications will be taken
into account ONLY if BaseSummary.dat and
AvailableReactionChart.dat have
been updated. You also need to remove the local ReactionList directory
(see after § 1.4.6).
Files of ``MURE/utils''
This directory contains codes that can be very helpful to users.
-
-
• ``endf2ace'' directory contains a small interface to NJOY
(see documentation in the directory)
-
-
• ``fp'' contains a utility to rebuild FPyield.bin
and FPavailable.dat of MURE/data directory. Main file
is GenerateFPYield.cxx which extracts from an ASCII ENDF file
(containing the FP yields) the fission product yield in a format used
by MURE.
-
-
• ``datadir'' contains programs that allows users to build
or complete the BaseSummary.dat and AvailableReactionChart.dat.
-
-
• ExtractXsdir.cxx allows users to build/complete a BaseSummary.dat
from an existing MCNP xsdir.
-
-
• ExtractTree.cxx allows users to build/complete a BaseSummary.dat
from a directory tree of cross-sections ; this tree can be built
by the ``endf2ace'' utility. The form of the directory tree
is
-
- base_name/base_version/Z/AAA/Isomeric_state/temperature/bin/
where, for example, base_name=ENDFB, base_version=6.8,
Z=92, AAA=235, Isomeric_state=0 (for ground
state), temperature=600 (in K). In the directory ``bin''
one find the binary cross-section of the desired nucleus in the file
``ace'' and an xsdir line for this nucleus in a file named
``dir'' (for example the line looks like '92235.10c
233.025000 ace 0 2 1 621851 4096 512 5.1704E-08 ptable')
In both cases, the compilation line is at the end of the source code.
NOTE: If an existing BaseSummary.dat is already present
in MURE/utils/datadir, this file is completed ; otherwise it
is created.
-
-
• CheckReaction.cxx must be used after building/modifying the
BaseSummary.dat file in order to build the AvailableReactionChart.dat.
NOTE: After running ExtractXsdir/ExtractTree and CheckReaction,
you have to copy the BaseSummary.dat and AvailableReactionChart.dat
in your MURE/data.
Graphical User Interface ``MURE/gui''
The GUI of MURE is located in the MURE/gui directory. The executable
name is ``MureGui'' and it reads the result of a MURE or Dragon
evolution. To use it, user must install ROOT (free download at http://root.cern.ch).
Before compiling MureGui, user has to edit the Makefile to set/unset
the LAPACK variable depending on whether he want to compute radiotoxicity
or not. To allow radiotoxicity calculation, the Lapack package must
be installed (see http://www.netlib.org/lapack/index.html)1.7. Then the compilation is obtained by a ``make'' in the MURE/gui
directory. Using MureGui without argument gives a short description
of the code used (see also § 7.3).
The MURE source files are located in ``MURE/source/include''
for the header files (.hxx) and in ``MURE/source/src''
for implementation (.cxx). When user is modifying the MURE
source, he has to recompile the MURE package (by a ``make''
in MURE/source/src). In MURE/source/external, one finds
2 auxiliary libraries, ValErr and Mctal that are
used in MURE. The ValErr defines a class to handle numbers
and their errors, and Mctal is dedicated to reading/writing
MCNP ``m'' files.
In any program using MURE, you have to include at
least:
-
- #include "MureHeaders.hxx"
and if needed,
-
- #include <libmctal/TMTally.hxx>
#include <libmctal/TMComment.hxx>
#include <libmctal/TMctal.hxx>
Other files
Each time a new evolution is run, a directory ReactionList
is locally built (if it is not already there) with the available reaction
of user's nuclear data base (one binary file for each Z). A list of
suppressed reactions for some of the nuclei (because they are lower
than a given threshold) is also written in ReactionList/SuppressReaction.dat.
The aim of theses files is to save time when using
the same nuclear data base AND the same reaction threshold, life-time
cutting and so on. Thus if you modify one of these, DO NOT
FORGET to remove the ReactionList directory.
-
-
• November 2014:
-
-
• Add the possibility to use standard MCNP tallies 238U and multi-group
tallies for other nuclei (see 5).
-
-
• October 2014:
-
-
• Add an optional equilibrium treatment for 135Xe (see 6.7)
-
-
• April 2013:
-
-
• Version of base and isomeric states (metastable and ground state)
for 242Am in BaseSummary.dat file for standard library
(distributed with MCNP or available@NEA) are now more
conform to the reality ; you have to regenerate your BaseSummary.dat/AvailableReaction.dat
files with the exec of MURE/utils/datadir. DON'T
FORGET TO REMOVE YOUR ReactionList
DIRECTORY IN ORDER TO TAKE INTO ACCOUNT THESE MODIFICATION.
-
-
• BasePriority has been debug and it seems to work as
expected...
-
-
• March 2013:
-
-
• Add a generalization of the MURE::SetMode() method to allow
any type of particle transport (mainly for MCNPX)
-
-
• Cell importance may have different value for each transported particles
(by successive call to Cell::AddParticle method)
-
-
• extend the MCNPSource possibilities (particle distributions
are now allowed for MCNPX)
-
-
• July 2012:
-
-
• Generalization of isomer production by
(n, γ) for special cases
(such as 241Am, 109Ag, ...), and bug correction
in (242Cm, 242Pu) production, see 5.1.6.
-
-
• Improve MurGui Spectrum radiotoxicity tab
-
-
• Allow to plot neutron balance in the ``Reaction Rate''
tab.
-
-
• June 2012:
-
-
• Add functionalities in MureGui (see MureGui's Radiotoxicity
tab)
-
-
• Nuclei extraction is now possible after a given cooling time.
-
-
• γ,
β, α and neutron spectra for evolving materials
can be computed.
-
-
• New MURE install procedure (more simple, more robust):
any fresh install or update NEED to run first the install.sh script
(require bash shell).
-
-
• Add the possibility to used multi-threading (OpenMP) during
the evolution and for updating multigroup
σφ when the gcc
version support this option (see INSTALL procedure and install.sh
script and section 6.2.2.2).
-
-
• Add some new kind of MCNPSource (see section 4.2.2)
-
-
• Add fluence to dose conversion for tallies
-
-
• May 2011:
-
-
• Add a new class GammaSpectrum class (section 7.4.2)
-
-
• New option of MureGui : use the ``radiotoxicity tab''
of MureGui on a dumped Material created with MURE (see
7.3.6 and ``MURE/example/GammaSpectrumExample.cxx'')
-
-
• New methods MCNPSource::SetAXS and MCNPSource::SetVec
allows user to define collimated sources.
-
-
• In Tally::Tally(int type,const char *particle) : if type < 0 , it's
change the Tally units.
-
-
• For example Tally *t=new Tally(-4,''P'') define a tally in
MeV/cm2
rather than
Particles/cm2 .
-
-
• A new method MURE::SetModeP() can be used to allow only the photon
transport.
-
-
• July 2009:
-
-
• Improve the english in User Guide: many thanks to Erica Agostinho
for this painful work.
-
-
• Implementation of PseudoMaterial: in order to take into account
temperature effects, one can process the nuclear data at the desired
temperature (using NJOY) or use an interpolation between 2
already existing temperatures ; this later method is used in the
PseudoMaterial techniques.
-
-
• Avril 2009: MURE is available at NEA DataBank
-
-
• January 2009:
-
-
• Improve reading time of BaseSummary.dat file : it is now greatly
recommended that this file is ordered by Z,A,I (this is the case if
it is generated by ExtractedXsdir.cxx and ExtractTree.cxx).
-
-
• Rewrite long parts of the documentation (User Guide and HTML
class description)
-
-
• Modify examples directory: it now contains documented examples and
output.
-
-
• November 2008: Improve radiotoxicity post treatment in MureGui.
-
-
• September 2008: Implement ``multigroup'' calculation for reaction
rates: a very narrow energy binning for flux calculation is put in
each MCNP run ; then reaction rates are obtained by reading
ACE MCNP files after each MCNP run. The result of such
method saves a considerable amount of CPU time for MCNP (at
least a factor 30) with only a low percentage of discrepancy (∼1
to 3%) in result compared to the standard calculation (reaction rates
are tallied in MCNP).
-
-
• April 2008:
-
-
• implementation of Predictor-Corrector method in the evolution
-
-
• possibility to read ASCII nuclear data file (ACE format): this avoids
problems due to binary compatibility (size of real (float or double?),
little or big endian, ...). BUT it is much longer to (1) build the
ReactionList directory and (2) run a MCNP.
-
-
• December 2007:
-
-
• Disable the
σφ extrapolation by default.
It has been shown, but not really understood, that this treatment
introduces a larger dispersion in the result, after N identical evolutions,
than doing nothing (no
σφ extrapolation).
-
-
• Modify the evolution using a MCNP User Input geometry file:
-
-
• ``like but'' cells can be used (but not evolved)
-
-
• ``MCNP Transformation'' cards can be used
-
-
• the 3rd block of the MCNP file is read and copied except the materials
(that must be defined in the MURE file). Thus the source as
well as all other cards of this block can be used without defining
them in the MURE file (this is also true for user defined tallies).
-
-
• October 2007:
-
-
• Switch from ccdoc to Doxygen for class documentation
-
-
• Change completely the MURE directory trees
-
-
• NON BACKWARD COMPATIBILITY
-
-
• Material definition has changed: now only 2 constructors must be used:
-
-
• Material(): for standard material (you have to specify density,
... with the Set methods)
-
-
• Material(int): for using materials from an MCNP input
file geometry.
-
-
• THE COPY CONSTRUCTOR HAS NOT TO BE CALL: CALL only the Material::Copy().
-
-
• The Material::Mix has been modified (number of arguments, units
required). see Material.hxx
-
-
• The Material::AddNucleus has been modified (number of arguments).
By default the proportion units are "kpMOL"
(i.e. molar proportion). But the unit must be specified if you use
a moderator (MT card of MCNP).
-
-
• The proportion units (both for Density and Proportion) must be used
for any Material::GetProportion() and Material::GetDensity()
methods
-
-
• for Proportion the only valid units are: kpMOL(molar prop),
kpMASS (mass prop), kpATCM3 (at/cm3), kpATBCM(at/barn.cm)
-
-
• for density the only valid units are: kdGCM3 (g/cm3), kdATCM3
(at/cm3), kdATBCM (at/barn.cm)
-
-
• A new material has been defined : ControlMaterial (public of
Material). This class is used for Poison, Fissile or other control
of reactivity (e.g. poison.cxx in MURE/examples)
-
-
• All Print() methods now return a string instead
of a void: to use them: cout<<Mat->Print()<<endl;
for example.
-
-
• EvolutionControl class has been cleaned (as well as MURE
class). If you want to use special control you have to write your
own derivative class. Examples using PoisonControl, FissileControl
& HNControl (but Adrien you have to rewrite them and look
carefully at TMSR.cxx in MURE/examples.) and Rod control
are defined in source/src. You can used them as they are or
defined your own using these examples.
-
-
• Almost all cout/cerr have been removed from classes; used instead
LOG_DEBUG, LOG_INFO, ... ; LOG_INFO is now
independent of LogLevelMessage ; it is always printed. If MURE::SetMessageLevel
is set to LOG_LEVEL_DEBUG, all LOG_DEBUG are printed.
But if MURE::SetSilentDebug is used, only the LOG_DEBUGs
of methods where a "int DODEBUG=1"
is inserted are printed. Thus, using LOG_DEBUG, avoids to
comment all "cout" when no debugging
is desired.
-
-
• ALL EXAMPLES HAVE BEEN UPDATED TO TAKE INTO ACCOUNT THESE MODIFICATIONS:
please READ THEM!!!!!!!!!!
-
-
• September 2007:
-
-
• Correct an important bug in evolution using an MCNP User Input
geometry file: number of Materials were not correct (Thanks to Jan
Frybort).
-
-
• Juin 2007:
-
-
• Rename the MURE header file Shapes.hxx into
MureHeaders.hxx : this is more logical...but you have to change your
MURE files....
-
-
• Add a new class EvolutionWrapper to simplify and extend EvolutionControl
capabilities
-
-
• Suppress the writing of BDATA_xxx and DATA_xxx ; now,
by default, only BDATA_xxx are written. This can be changed
using the MURE::SetWriteBinaryData() and MURE::SetWriteASCIIData()
methods.
-
-
• One can start an evolution from a given step : suppose that the evolution
stops at step i ; an evolution can be started from the step
i+1 using MURE::Evolution(T,i+1). Warning: it is probably
not correct for OutCoreEvolutiveSystemVector...you must do
the evolution from the first step as before.
C++ logic for building geometries is slightly different for the MCNP
one ; therefore, each time a new geometry is built you should check
it with MCNP before using it.
There are two base classes to build a geometry: Shape and Cell.
Shape describes only geometrical shapes, and Cell corresponds
to an MCNP cell (i.e., it has a material, importance, etc.).
Shape objects correspond to simple geometrical shapes (sphere, plane,
...) as well as more complex ones resulting from the intersection
and/or union of simple shapes (Intersections/unions are defined by
the Node class). A Node is a ``tree'' of intersections/unions
of Shapes. For fast calculations, a node tree has to be as simple
as possible. Special methods are available for simplifying the node
trees which can (in general) determine whether or not a Shape is disjointed
(or included) of (in) another Shape (see example in figures B.1
to B.4 in Appendix B).
These simplifications may result in the deletion of some Shapes. But,
because one must not destroy a Shape in a Node if that Shape belongs
to another Node, a special way to handle Shape creation/destruction
has been implemented (via Reference_ptr).
In conclusion : the user must only
use Shape_ptr (a ``reference Shape'') and not Shape. Shape_ptr
is a pointer to Shape with Reference_ptr. In that way, the Shape_ptr
will be destructed only if it is no longer referenced, otherwise,
its ``deletion'' leads to a decrementation of the number of references.
-
-
• There are 4 available base Shapes
:
-
-
• Plane (infinite),
-
-
• Cylinder (infinite),
-
-
• Sphere,
-
-
• Brick (finite or infinite)
-
-
• Then one can define Node
(unions or intersections of Shapes) with 2 already defined Nodes:
-
-
• Tube
-
-
• Hexagon (finite or infinite)
A Brick is a rectangular parallelepiped. A Tube is a
finite cylinder with an optional inner radius that defines a ``tube''.
Hexagons can have finite or infinite height. In general, a
user will only need to use Spheres, Bricks, Tubes
and Hexagons.
One can define the interior or the exterior of each Shape.
The complement of a Shape can be defined by the Not() method
as well as by the ``!'' operator (see examples given later on).
Other shapes available in MCNP(X) may be added by any user. This is
not too hard even if it requires some work. The best way to do it,
is to read the implementation of existing shapes to have an idea.
WARNING: In MURE, the length unit is the meter (whereas
in MCNP it is the cm). In particular, volumes in MURE are in m3.
| Length |
m |
| Energy |
eV |
| Temperature |
K |
| Density |
g/cm3, atom/cm3 or atom/(barn.cm) |
| Proportion |
%mol, %mass, atom/cm3 or atom/(barn.cm) |
To define the interior of a origin center sphere of radius R:
-
- Shape_ptr S(new Sphere(R));
To define the outer part of S one can do
-
- Shape_ptr Ext_S(!S);
or
-
- Shape_ptr Ext_S(S->Not());
or
-
- Shape_ptr Ext_S(new Sphere(R,0,0,0,1);
where 3 zeros correspond to the sphere center (the origin) and +1
to the exterior of the Sphere (default=-1).
For Hexagons and Bricks, two versions exist: finite
or infinite Shapes. For finite bricks and hexagons, you should
define it as:
-
- Shape_ptr B(new Brick(HalfX, HalfY, HalfZ, Signe));
Shape_ptr H(new Hexagon(HalfHeight, Side, Signe));
where HalfX (resp. Y and Z) is the Half length of the brick in the
X (resp. Y and Z) direction, HalfHeight the half height (!) of the
hexagon, Side its side, and Signe the sign defining whether it is
the inner or the outer part, just as for the sphere. For infinite
ones, to avoid conflicts between the definitions, a string at the
beginning is necessary (and, of course, HalfHeight and HalfZ are irrelevant)
:
-
- Shape_ptr B(new Brick(``any string you want'', HalfX, HalfY, Signe));
Shape_ptr H(new Hexagon(``any string you want'', Side, Signe));
The infinite shapes obtained are parallel to the Z axis, but they
may be rotated afterwards.
A Node is the Union (+1) or the Intersection (-1) of Shapes (i.e.,
simple Shapes or Nodes).
To define the intersection of a sphere centered at (
x0, y0, z0)
of radius R with a square brick of side a centered at the origin,
one may use:
-
- Shape_ptr S(new Sphere(R,x0,y0,z0);
Shape_ptr B(new Brick(a/2,a/2,a/2));
Shape_ptr Inter=S & B;
whereas the union of the sphere and the brick may be defined as
-
- Shape_ptr Union=S | B;
It is possible to move (translation/rotation) a Shape (or a
Node) via the Shape::Translate and Shape::Rotate
methods. For example, to translate the Shape_ptr B of (dx,dy,dz),
-
- B->Translate(dx,dy,dz);
and to rotate clockwise B around (
x0, y0, z0) of φ,
θ and ψ around the z, y and x axis respectively:
-
- double center[3]={x0,y0,z0};
B->Rotate(phi,theta,psi,center);
Note that the translation/rotation of a Shape translates/rotates also
the inside shapes (see next section).
It is possible to put a Shape_ptr A inside another B one,
via the ``put in''3.1 operator A>>B ; this operator
works differently depending on A:
-
-
• if A is a normal Shape_ptr: a A>>B modifies
both A and B ; A becomes A∩B and B becomes B∩!A (see
figure 3.1)
Figure 3.1:
Operator >> (put in). (a) A and B before the action
of the operator ; (b) A and B after the action of the operator.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=10cm]{fig/put_in}
\par
\end{centering}\par
\protect
\end{figure}](Timg3.gif) |
-
-
• if A is a Shape_ptr with a universe number (e.g. after a call to
Shape_ptr::SetUniverse() for a lattice): A>>B
does not modify neither A nor B ; a MCNP Fill card is just added to
B in order to fill B with universe of A.
Example:
-
- Shape_ptr S(new Sphere(R));
Shape_ptr B(new Brick(a/2,a/2,a/2));
B>>S;
In this example, the Brick B is put inside S.
Note that now S and B are new Shape_ptr: S=S & !B (i.e. the
sphere without the brick) and B=S & B (i.e, the intersection of the
brick and the sphere) as already mentioned above (see fig. 3.1).
-
-
• The brick B is an inside shape of S: this means that
if one moves S, one moves also B.
-
-
• It is possible to link inclusion:
-
- A>>B>>C;
means that A is put in B and the result is also put in C.
A is an inside shape of B and C ; B is an inside shape of C.
-
-
• if after the previous example, one makes
-
- C>>D;
Inside shapes of C are cleared and D has A, B and C as Inside
Shapes.
It may be sometimes very useful to clone a Shape, i.e., to
create a new Shape with the same properties as the original
one. Here is an example:
-
- Shape_ptr B1(new Tube(1,0.5));
Shape_ptr T1(new Tube(1,0.4));
Shape_ptr T2(new Tube(1,0.3));
T2>>T1>>B1;
Shape_ptr B2=B1->Clone();
B2->Translate(1,0,0);
B2 has exactly the same aspect as B1 (with 2 tubes inside) but it
is translated by 1m in the x direction, whereas B1 is centered
at the origin.
In MCNP, it is possible to use special boundary conditions: mirror,
white or periodic boundary conditions. In MURE, these boundary conditions
could be used but have not been fully tested...so it is advised to
use them carefully. In all cases, the exterior of the Shape_ptr with
boundary conditions must have a zero importance. You can apply only
one type of boundary conditions to a Shape_ptr. Here is a brief description
of these boundary conditions:
-
-
• Mirror conditions correspond to a standard reflexion on a shape ;
the method to define such conditions is
-
- Shape_ptr A(...);
A->SetMirrorBoundary();
-
-
• White conditions correspond to a reflexion with a cosine direction
distribution on the surface ; the method to define such conditions
is
-
- Shape_ptr A(...);
A->SetWhiteBoundary();
-
-
• Periodic condition: when a particle leaves a given plane it re-enters
through another one. This method could only be applied to Bricks or
Hexagons, with the restriction that the Top and Bottom planes (before
any reflexions) are either Mirror boundaries, White boundaries or
Infinite boundaries.The method to define such conditions is
-
- Shape_ptr A(new Brick(1,1,1));
A->SetPeriodicBoundary(true,"mirror");
or
-
- Shape_ptr A(new Brick(1,1,1));
A->SetPeriodicBoundary(true,"white");
-
-
• It is generally simpler to define a geometry from
the inner part to the outer part : for example,
-
-
• define first shape A, then B and C and D.
-
-
• Put shapes inside each other like
-
- A>>B>>D;
C>>D;
-
-
• After doing that, you can't move and/or rotate
A, B or C. But if you move/rotate D, then it will move/rotate also
the inner shapes (A, B and D). If A, B or C have to be rotated or
translated to a given position in D, then you must do it BEFORE putting
these shapes inside D.
-
-
• Avoid complex shapes: it is more efficient (in term
of CPU time in MCNP) to
divide a complex in several simpler shapes.
A Cell is defined by a Shape_ptr, and if needed
a Material.
MCNP cells are defined via the Cell
class ; one has to give
-
-
• the Shape_ptr corresponding to the geometric shape of the Cell,
-
-
• the Material (see section 4.1) if exists
(default=0 for void),
-
-
• the importance of particles3.2 (default=1),
-
-
• a lattice, if needed.
For example to construct a cell composed of a full tube of radius
R and height H, made of B4C
-
- Shape_ptr C(new Tube(H/2,R));
Cell *c=new Cell(C,B4C);
where B4C is a (Material*)3.3. In this example, one can define the exterior cell as
-
- Shape_ptr Exterior(!C);
Cell *exterior=new Cell(Exterior,0,0);
The first zero means that the material is void and the second one
means that neutron importance is set to 0 in the exterior cell.
If not only neutrons are transported in MCNP, it is useful to define
the desired mode (i.e., NP, NE, NPE for Neutron and Photon, Neutron
and Electron and Neutron, Photon and Electron) before any Cell definition ;
indeed, in this case, the given cell importance applies to all particle
types. For example:
-
- gMURE->SetModeNP();
Cell *c=new Cell(C,B4C);
Cell *exterior=new Cell(Exterior,0,0);
will set the transport mode to neutrons and photons and the cell c
will have an IMP:N=1 and IMP:P=1 whereas the cell exterior
will have an IMP:N=0 and IMP:P=0.
Suppose we have defined 2 tubes B1 and B2 as follows:
-
- Shape_ptr B1(new Tube(1,0.5));
Shape_ptr T1(new Tube(1,0.4));
Shape_ptr T2(new Tube(1,0.3));
T2>>T1>>B1;
Shape_ptr B2=B1->Clone();
B2->Translate(1,0,0);
the cell definition for B1 is not a problem:
-
- Cell *b1=new Cell(B1,Graphite);
Cell *t1=new Cell(T1,Iron);
Cell *t2=new Cell(T2);
where Graphite and Iron are two Material*. Here, the result
will be a tube of graphite containing a tube of iron containing a
void tube. To define analog cells for B2 we have to do:
-
- Cell *b2=new Cell(B2,Graphite);
Cell *tt1=new Cell(B2->GetOriginalInsideShape(1),Iron);
Cell *tt2=new Cell(B2->GetOriginalInsideShape(0));
Indeed, the ``Inside shapes'' of B2 are ordered from the most inner
(B2->GetOriginalInsideShape(0) clone
of T2), to the most outer (B2->GetOriginalInsideShape(1)
clone of T1).
Lattices are used in MCNP to fill cells of repeated structure. There
are 2 types of lattice, hexahedra (type=1) or hexagonal (type=2).
In this section, four examples of lattices are presented (from the
most simple to the most complex case). Of course the lattice type
does not change the declaration (except that the lattice generator
is a Brick for hexahedra lattice whereas it is an Hexagon
for the type 2).
The general philosophy for lattice declaration is the following:
-
-
• In the Shape section
-
-
• define the Shape_ptr A that will be filled by the lattice,
-
-
• define the Shape_ptr G that is used as lattice generator (a
Brick or an Hexagon) and give to that generator a universe number
(via Shape::SetUniverse()),
-
-
• put G in A with G>>A
-
-
• define all Shape_ptr Bi that shall be used in the lattice
and assign them a universe number (via Shape::SetUniverse()).
-
-
• In the Cell section
-
-
• build the Cell for Shape_ptr A
-
-
• build the Cell of the generator Shape_ptr G
-
-
• indicate to cell of Shape G that it is a Lattice (via Cell::Lattice())
-
-
• fill the lattice with all the desired Shape_ptr Bi (via
Cell::FillLattice())
A simple lattice example (SimpleLattice.cxx)
This example is a simple tube which is filled by an hexagonal lattice
(type 2). Each hexagon of the lattice is made of graphite and filled
with a small tube of Iron.
-
- //
// define materials (see § 4.1)
//
Material *Iron=new Material();
Iron->SetDensity(7.87);
Iron->AddNucleus(26,56,1.);
Material *Graphite=new Material();
Graphite->SetDensity(1.86);
Graphite->AddNucleus(6,0,1);
//
// define geometrical Data size
//
double VesselH=2;
double VesselR=1;
double HexaH=VesselH;
double HexaSide=0.2;
double PinH=VesselH;
double PinR=0.05;
//
//Shapes
//
//the Vessel : a full Tube
Shape_ptr Vessel(new Tube(VesselH/2,VesselR));
//the Exterior
Shape_ptr Exterior(!Vessel);
//the lattice generator
Shape_ptr LatticeGenerator(new Hexagon(HexaH/2,HexaSide));
LatticeGenerator->SetUniverse();
LatticeGenerator>>Vessel; // put Lattice Generator in the vessel
// a small full tube that will fill the lattice
Shape_ptr Pin(new Tube(PinH/2,PinR));
Pin->SetUniverse();
//
//Cells
//
Cell *exterior=new Cell(Exterior,0,0);
exterior->SetComment("The exterior of the cylinder");
//vessel
Cell *vessel=new Cell(Vessel);
vessel->SetComment("The vessel");
//the lattice
//---------- Line A ----------
Cell *Pavage=new Cell(LatticeGenerator);
Pavage->Lattice(2); // define a hexagonal lattice
Pavage->FillLattice(Pin); //fill the lattice with the iron Pin
//---------- Line B ----------
//the pin and its exterior that define a second universe
Cell *pin=new Cell(Pin,Iron);
Cell *exterior_pin=new Cell(!Pin,Graphite);
The result is shown in Figure 3.2.
Figure 3.2:
A simple lattice.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=8cm]{fig/simpleLatt}
\par
\end{centering}\par
\protect
\end{figure}](Timg4.gif) |
-
-
• In the Shape part:
-
-
• a lattice generator shape is defined,
-
-
• and the method Shape::SetUniverse() is used to give a universe
number to that Shape.
-
-
• Then, this generator is put in the ``Vessel''.
-
-
• We define a small tube and assign it a universe number.
-
-
• In the Cell part:
-
-
• the Pavage cell is declared with the lattice shape generator, made
of void.
-
-
• The Lattice type is set to hexagonal via Cell::Lattice().
-
-
• The whole Pavage cell is filled with the small tube universe number.
-
-
• Then this universe is constructed (Cells pin and exterior_pin). Note
that Pin Shape and !Pin have the same universe number.
A lattice with different zones (SimpleLattice2.cxx)
Let us modify the previous example slightly: we want to fill the Vessel
with 2 types of hexagons: the first ones are full graphite hexagons
(the reflector) in the outer part of the Vessel and the second ones
are the previous hexagons with the small rod inside that fills a virtual
inner cylinder of radius 80cm. The only change takes place between
the lines named ``Line A'' and ``Line B'' . We have to replace
this part by:
-
- //---------- Line A ----------
Cell *Pavage=new Cell(LatticeGenerator,Graphite);
int range=int(VesselR/(1.5 * HexaSide))+1;
Pavage->Lattice(2,-range,range,-range,range); //define a explicit lattice
for(int i=-range; i<=range; i++)
for(int j=-range; j<=range; j++)
{
int pos[3]={i,j,0}; //the lattice index
double xt = HexaSide*sqrt(3.) * (i + j*0.5 ) ;
double yt = 1.5 * HexaSide * j;
double X[2]={xt,yt}; //the center of each hexagons
if(IsHexagonInTube(X,LatticeGenerator,0.8)) //true if the hexa center at X is
Pavage->FillLattice(Pin,pos); //inside a tube of radius 80cm
}
//---------- Line B ----------
-
-
• The Pavage Cell is now made of graphite in order to fill the empty
hexagons of the lattice (the so called ``reflector'') with this
material.
-
-
• Then the hexagonal lattice is defined as (2range×2range)
matrix (in x and y direction and infinite in z).
The ``range'' has been defined to fill the whole vessel.
-
-
• Then, each position of hexagons in the lattice is computed ; if a
hexagon is completely inside the virtual cylinder of radius 0.8m,
a hexagon with the small iron tube is added (Cell::FillLattice)
at the given position pos.
The result is shown in Figure 3.3.
Figure 3.3:
A lattice with different zones .
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=8cm]{fig/simpleLatt2}
\par
\end{centering}\par
\protect
\end{figure}](Timg5.gif) |
Note that in this example, there is no way to obtain a tally only
in ``the reflector'' part, because it is only a part of the Cell
``Pavage''. In order to obtain such information, the quicker
way is:
-
-
• In the Shape part, define a Shape_ptr corresponding
to the Whole space (intersection of nothing3.4):
-
- Shape_ptr Whole(new Node(-1));//-1=intersection, here, of nothing
Whole->SetUniverse();
-
-
• In the Cell part, replace the line
-
- if(IsHexagonInTube(X,LatticeGenerator,0.8))
Pavage->FillLattice(Pin,pos);
by
-
- if(IsHexagonInTube(X,LatticeGenerator,0.8))
Pavage->FillLattice(Pin,pos);
else
Pavage->FillLattice(Whole,pos);
and add the following Cell
-
- Cell *whole=new Cell(Whole,Graphite);
A lattice with more than one simple shape (Stadium.cxx)
In this example, we consider a hexahedra lattice (type 1). Each brick
of the lattice will have parts of ``stadiums'' on each (x,y) sides
(see Figure 3.4, this is the base geometry of
the MSRE reactor).
-
- //
//materials
//
Material *Iron=new Material();
Iron->SetDensity(7.87);
Iron->AddNucleus(26,56,1.);
Material *Graphite=new Material();
Graphite->SetDensity(1.86);
Graphite->AddNucleus(6,0,1);
//
// Data
//
double VesselH=0.8; // the core H and R
double VesselR=0.4;
double SquareH=VesselH; //stadium heigth
double SquareS=0.2; //stadium straight line length
double BendR=0.02; //stadium bend curve radius
double BendH=VesselH;
double BrickW=0.04;
double BrickL=0.08;
//
//Shapes
//
//the Vessel
Shape_ptr Vessel(new Tube(VesselH/2,VesselR));
//the Exterior
Shape_ptr Exterior(!Vessel);
//the lattice generator
Shape_ptr LatticeGenerator(new Brick(SquareS/2,SquareS/2,SquareH/2));
LatticeGenerator->SetUniverse();
//put the lattice generator inside the core
LatticeGenerator>>Vessel;
//Definition of the stadiums (horizontal & vertical)
Shape_ptr Circle0(new Tube(BendH/2,BendR));
Circle0->SetUniverse();
//clone circles for horizontal and vertical stadiums
Shape_ptr Circle1=Circle0->Clone();
Shape_ptr Circle2=Circle0->Clone();
Shape_ptr Circle3=Circle0->Clone();
//translate circle
Circle0->Translate(-0.1,+0.04,0);
Circle1->Translate(-0.1,-0.04,0);
Circle2->Translate(-0.04,0.1,0);
Circle3->Translate(+0.04,0.1,0);
//2 bricks for horizontal and vertical stadiums
Shape_ptr Brick0(new Brick(BrickW/2,BrickL/2,SquareH/2));
Brick0->SetUniverse(Circle0->GetUniverse()); //belong to the same universe than Circle0
Brick0->Translate(-0.1,0,0);
Shape_ptr Brick1(new Brick(BrickL/2,BrickW/2,SquareH/2));
Brick1->SetUniverse(Circle0->GetUniverse()); //belong to the same universe than Circle0
Brick1->Translate(0,0.1,0);
//2 vertical stadiums
Shape_ptr Stade0=Circle0 | Brick0 | Circle1; //union of circles and brick
Shape_ptr Stade2=Stade0->Clone();
Stade2->Translate(0.2,0,0);
//2 horizontal stadiums
Shape_ptr Stade1=Circle2 | Brick1 | Circle3;
Shape_ptr Stade3=Stade1->Clone();
Stade3->Translate(0,-0.2,0);
//interior of all stadiums
Shape_ptr AllStades=Stade0 | Stade1 | Stade2 | Stade3; //to define all stadium exterior
//
// Cells
//
Cell *exterior=new Cell(Exterior,0,0);
exterior->SetComment("The exterior of the reactor");
//vessel
Cell *vessel=new Cell(Vessel,Graphite);
vessel->SetComment("The reactor vessel");
//Lattice
Cell *Pavage=new Cell(LatticeGenerator,Graphite);
Pavage->Lattice(1); //hexahedral lattice
Pavage->FillLattice(Stade0);
Pavage->FillLattice(Stade1);
Pavage->FillLattice(Stade2);
Pavage->FillLattice(Stade3);
Cell *stade0=new Cell(Stade0,Iron);
Cell *stade1=new Cell(Stade1,Iron);
Cell *stade2=new Cell(Stade2,Iron);
Cell *stade3=new Cell(Stade3,Iron);
Cell *exterior_stade=new Cell(!AllStades,Graphite);
-
-
• In the Shape part:
-
-
• A Tube (Circle0) is created at the origin ; then it is cloned
in 3 other Tubes (universe number of Circle0 is given to its
clones). Then these Tubes are translated to the right place.
-
-
• 2 Bricks are created (with the same universe as Circle0) and
translated to the left and the top of the square.
-
-
• Then 2 stadiums are constructed as the union of 2 tubes and a brick.
The right and bottom stadiums are cloned from the 2 previous ones,
and a union of all stadiums is constructed.
-
-
• In the Cell part:
-
-
• The lattice cell is defined, set to type 1, and each stadium is added
to the lattice.
-
-
• then, stadiums cells and exterior of these stadium, defining a unique
universe, are built.
Figure 3.4:
A lattice with more than one shape.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=8cm]{fig/complexLatt}
\par
\end{centering}\par
\protect
\end{figure}](Timg6.gif) |
Lattice of a Lattice (LatticeOfLattice.cxx)
The purpose of this example is to illustrate a hexagonal Lattice of
big structural hexagons, themselves filled with a hexagonal lattice
of fuel rods (like in a EFR/Superphenix core)
-
- double VesselH=1.1;
double VesselR=1.1;
double FuelHexaSide=0.05;
double BicR=0.01;
double StructHexaSide=8./sqrt(3)*FuelHexaSide;
double StructThick=0.01;
//the Vessel
Shape_ptr Vessel(new Tube(VesselH,VesselR));
//the Exterior
Shape_ptr Exterior(!Vessel);
//the outside structure hexagon
Shape_ptr StructHexa(new Hexagon(VesselH,StructHexaSide+StructThick));
StructHexa->SetUniverse();
//the inside structure hexagon
Shape_ptr InnerStructHexa(new Hexagon(VesselH,StructHexaSide));
InnerStructHexa->SetUniverse();
Shape_ptr Reflector(new Node(-1));
Reflector->SetUniverse();
StructHexa>>Vessel;
//
//a fuel hexagon
//
Shape_ptr FuelHexa(new Hexagon(VesselH,FuelHexaSide));
FuelHexa->Rotate(-Pi/6);
FuelHexa->SetUniverse();
FuelHexa>>InnerStructHexa;
Shape_ptr Carandache(new Tube(VesselH,BicR));
Carandache->SetUniverse();
Shape_ptr SideStructNeighbourg(new Node(-1));
SideStructNeighbourg->SetUniverse();
//============================================================
// Cells
//============================================================
Cell *exterior=new Cell(Exterior,0,0);
exterior->SetComment("The exterior of the reactor");
Cell *vessel=new Cell(Vessel);
vessel->SetComment("The reactor vessel");
Cell *structhexa=new Cell(StructHexa);
structhexa->SetComment("The Outside struct Hexa");
int range1=int(VesselR/(1.5 * StructHexaSide)+1);
structhexa->Lattice(2,-range1,range1,-range1,range1);
double StructHexaWidth=sqrt(3)*StructHexaSide;
for(int i=-range1; i<=range1; i++)
for(int j=-range1; j<=range1; j++)
{
int pos[3]={i,j,0};
double xt = StructHexaWidth * (i + j*0.5 ) ;
double yt = 1.5 * StructHexaSide * j;
double X[2]={xt,yt};
if(IsHexagonInTube(X,StructHexa,VesselR))
structhexa->FillLattice(InnerStructHexa,pos);
else
structhexa->FillLattice(Reflector,pos);
}
Cell *reflector=new Cell(Reflector);
Cell *innerstructhexa=new Cell(InnerStructHexa);
innerstructhexa->SetComment("The Inside struct Hexa");
Cell *exterior_innerstructhexa=new Cell(!InnerStructHexa);
Cell *core=new Cell(FuelHexa);
int range=int(StructHexaSide/(1.5 * FuelHexaSide)+1);
core->Lattice(2,-range,range,-range,range);
double FuelHexaWidth=sqrt(3)*FuelHexaSide;
for(int i=-range; i<=range; i++)
for(int j=-range; j<=range; j++)
{
int pos[3]={i,j,0};
double xt = 1.5 * FuelHexaSide * i ;
double yt = FuelHexaWidth * ( j + i*0.5 );
double X[2]={xt,yt};
if(IsHexagonInHexagon(X,FuelHexa,InnerStructHexa))
core->FillLattice(Carandache,pos);
else
core->FillLattice(SideStructNeighbourg,pos);
}
Cell *carandache=new Cell(Carandache);
Cell *exterior_carandache=new Cell(!Carandache);
Cell *sidestructneighbourg=new Cell(SideStructNeighbourg);
Figure 3.5:
Lattice of a Lattice.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[scale=0.8]{fig/latoflat}
\par
\end{centering}\par
\protect
\end{figure}](Timg7.gif) |
Definition of material
A Material
is a set of nuclei with their proportions, it has a density and a
temperature.
For example to define B4C of density 2.52 g/cm3at 296 K:
-
- Material *B4C=new Material();
B4C->SetDensity(2.52); //default units are g/cm3
B4C->AddNucleus(5,10,0.199); //Boron is composed 19.9% of
510B
B4C->AddNucleus(5,11,0.801); // and 80.1% of
511B
B4C->AddNucleus(6,0,0.25); // This is natural C (Z=6, A=0) ; for 1 mol of B one has 0.25 mol of C
At the end (i.e. when a Material is written in MCNP file, proportions
are normalized to 1). The Material::AddNucleus() method has
the general form
-
- Material::AddNucleus(Z,A,I,prop);
or
-
- Material::AddNucleus(Z,A,prop);
where Z is an integer corresponding to the proton number of
the nucleus, A, an integer for the number of nucleons, I,
an integer for the isomeric state and prop, a double for the
proportion of the nucleus in the Material. For natural
isotopes A=0 ; for ground state I=0 (this is the default
value when not specified). See § 4.1.3 for
units.
-
-
• A Material can contain one nucleus which is a ``moderator'':
this means that the special treatment
S(α, β) is applied
for low energy in MCNP for this nucleus. In order to say that
a nucleus is a moderator, one has to add a string for the last parameter
of Material::AddNucleus (see 4.1.4 for
a full description) ; defining thermal treatment for hydrogen in
light water leads to:
H2O->AddNucleus(1,1,2.,kpMOL,"H2O");
//here the unit of proportion must be given explicitly
H2O->AddNucleus(8,16,1.);
A Material can be cloned via the Material::Clone(double Temperature)
method. There are 2 types of clones depending on:
-
-
• whether the material does not evolve and the Temperature
argument of Material::Clone() is negative (the default)
(see example of B4C_Light in § 4.1.7):
the clone is only used because it makes possible to define a material
with the same number in MCNP but also present at different
densities in different cells. A call to Material::SetTemperature()
will have no effect on such a clone!
-
-
• or whether the material will evolve and/or the Temperature
argument is positive or null (see example of Comb2
and B4C_Hot in § 4.1.7): the clone
is a ``true'' clone, i.e., all composition and proportions are duplicated
(2 different material numbers in MCNP). Of course the density,
temperature,... of the clone could be changed after cloning, as well
as new nuclei could be added. This kind of clone is the correct way
to handle 2 evolving cells starting with the same composition but
evolving independently. Note that by default the density of the clone
is the one of the original material.
Two Materials of different densities can be mixed together to create
a third material. This is useful in many situations, e.g., the case
of reactor fuels with a given enrichment of fissile isotopes. The
principle is the following:
-
- M3=M1->Mix(M2,part,kpMOL);
M3 is a new material and is created from the molar part mixture of
materials M1 and M2 (for example Uranium and Plutonium Oxides). If
M1 and M2 are not needed directly in the problem, it is important
to force them to be fictitious materials by using the Material::ForbidPrint()
method: THIS IS DONE IN THE Material::Mix()
METHOD. The density of the new material M3, if not specified by Material::SetDensity(),
is calculated as the linear interpolation between the densities of
M1 and M2. The temperature of the new material is the same as that
of material M1.
Units
Default units for density is g/cm3; but, to avoid confusion,
you must set the density unit in Material::GetDensity() (either
kdGCM3 (g/cm3), kdATCM3 (at/cm3) or kdATBCM
(at/barn.cm)). User may give the density in atom/barn.cm by using
Material::SetDensity(density,kdATBCM).
If the density is not given (i.e. set to the default
value 0), it could be automatically found if the proportions are given
in atoms/barn.cm or in atoms/cm3 .
Default units for proportions are in molar percentage. To give proportion
in other units, use
-
- Material::AddNucleus(Z,A,I,prop,UNITS)
where UNITS stands for kpMOL ("%mol"
(default)) or kpMASS ("%mass"
) or kpATBCM ("at/barn.cm") or
kpATCM3 ("at/cm3").
In MCNP, material codes have extensions (like ``.60c'').
These extensions are very important because they distinguish isotopes
at different temperatures, bases, versions,... In practice,
if no extension is specified in MCNP file, the first isotope
encountered in the xsdir is chosen regardless the temperature
imposed in the cell where the material is. In MURE user has
different ways to specify an extension.
-
-
• This can be done manually for each nucleus of the material
composition:
-
- mat->GetNucleus(Z,A,I)->SetXSExtension(".49c")
-
-
• This can be done manually for all nuclei of the material
composition:
-
- mat->SetDefaultXSExtension(".49c")
then each nucleus of the Material mat will have this ".49c"
extension.
-
-
• If the MCNP code for a particular Nucleus (Z,A,I) of a given
Material mat is known, it can be specified by using:
-
- mat->GetNucleus(Z,A,I)->SetXSExtension(".49c")
-
-
• This can be done automatically: the specific file, the so-called ``BaseSummary.dat''
file, which contains xsdir information written in a different way
for search efficiency, is used. The extension is chosen according
to the Material temperature. In fact the closest temperature
to the one of the Material is chosen with the help of classes
BasePriority and TemperatureMap. (see below)
-
-
• If evolution is need, the automatic procedure is certainly required...but
I am not sure (PTO).
-
-
• If one specifies the extension value (either via Nucleus::SetXSExtension()
or Material::SetDefaultXSExtension()
or Nucleus::SetModeratorName())
then you must provide in the xsdir the corresponding data files.
S
(α, β) Treatment and MT card
When the special treatment
S(α, β) is desired for low energy,
MCNP MT card arguments has to be specified. Consider
the water example:
-
- H2O->AddNucleus(1,1,2.,kpMOL,"H2O");
H2O->AddNucleus(8,16,1.);
-
-
• this can be done manually: the string ``H2O'' must not be empty ;
then
-
- H2O->GetNucleus(1,1)->SetModeratorName("lwtr.01t");
-
-
• this can be done automatically: the BaseSummary.dat file is
read to find the code of
S(α, β) treatment file ; this
time, because
S(α, β) treatment is material dependent,
the string has to refer to a given ''Category'' to specify which
kind of effects are taken into account ; in the above example, hydrogen
has different
S(α, β) treatment for light water, polyethylene,
benzene, ... The complete list of available Categories is given in
Nucleus
in the Nucleus::SetModeratorCategory():
| H2O |
for H in light water |
| H/Zr |
for H in ZrH |
| poly |
for H in polyethylene |
| D2O |
for D in heavy water |
| BeO |
for Be in Be oxide |
| Be |
for Be in Be metal |
| Gr |
for graphite |
| Zr/H |
for Zr in ZrH |
The moderator category can also be any real MT file
name such as ``lwtr'' or ``u/o2'', ...
PseudoMaterials are particularly useful for thermal-hydraulics
problems. Normally, the material temperature dictates which extension
(e.g. ``.60c'') for cross-sections will be used from the evaluated
data libraries. The default behvaiour in MURE is that
the nearest available temperature is used, the maximum tolerable difference
between this temperature and the desired material temperature being
defined in the TemperatureMap class. However, there are occasions
where it is useful to perform a stochastic interpolation at the desired
temperature by adding two identical nuclei at different temperatures
in the material in varying proportions. These types of materials are
called PseudoMaterials, because, in principle, they behave
as a material at a precise temperature, T, even though the cross-sections
in the evaluated data libraries at this precise temperature do not
exist. To declare a Material (Mat) to be a PseudoMaterial
requires the following simple line:
-
- Mat->SetPseudoMaterial();
From this point onward, MURE will automatically create
two identical nuclei with different extensions/temperatures and in
the correct proportions for, every nucleus which is added to this
material. No other commands are necessary. However, in the case of
an evolving material (a reactor fuel rod for example), this can cause
the addition of many, many extra nuclei to the material, thus slowing
down MCNP calculations by perhaps as much as 20%. In the case
that the user only wants to declare certain nuclei to be PseudoNuclei
(for example, the most important ones, such as the fissile and fertile
nuclei) the following kind of lines can be added after the creation
of a Material:
-
- UO2Fuel->AddNucleus(92,235,0.04);
UO2Fuel->AddNucleus(92,238,0.96);
UO2Fuel->AddNucleus(8,16,2.0);
UO2Fuel->GetNucleus(92,235)->SetPseudoNucleus();
UO2Fuel->GetNucleus(92,238)->SetPseudoNucleus();
Now, only the selected nuclei will be treated as pseudo nuclei and
automatically inserted twice into the MCNP file at the two
nearest data base temperatures in the correct proportions. The proportions,
ω1 and
ω2 , for the interpolation are calculated
in the following way:
ω2 = 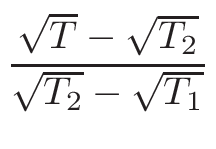
ω1 = 1 - ω2
where T1 and T2 are the nearest two temperatures in the
evaluated data base files straddling the desired temperature T.
MCNP material Printing
This section concerns only evolving Materials. When evolution is required,
at the beginning, many nuclei are present in the material but in a
very small proportion. Each time a neutron enters in a cell, MCNP
tries to find the nucleus on which the potential reaction could happen.
Thus, the bigger is a material, the longer is the MCNP run.
The idea is to suppress only for the MCNP print, the nuclei
which do not contribute to neutron transport to save time. The criterion
is based on the evaluation of total cross-section
σT and
nucleus proportion p. If a nucleus of a material has a
p×σT < 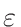 ,
it is not printed. The value of
,
it is not printed. The value of
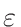 is by default set to
0.1%×1mb = 10-6. This can be changed via MURE::SetMCNPNucleusThreshold().
To be noticed that perturbative tallies of all evolving nuclei are
written (in order to evaluate the cross-section...). The effect of
this procedure is thus to accelerate MCNP runs at the beginning
of the evolution where time steps between MCNP are smaller,
and add more and more nuclei as far as the evolution is going on (with
bigger time steps between MCNP runs).
is by default set to
0.1%×1mb = 10-6. This can be changed via MURE::SetMCNPNucleusThreshold().
To be noticed that perturbative tallies of all evolving nuclei are
written (in order to evaluate the cross-section...). The effect of
this procedure is thus to accelerate MCNP runs at the beginning
of the evolution where time steps between MCNP are smaller,
and add more and more nuclei as far as the evolution is going on (with
bigger time steps between MCNP runs).
Examples
Please take a look at Material_test.cxx and Material_test2.cxx.
Here are some examples:
-
- //the Lead and its extension
Material *Lead=new Material();
Lead->SetDensity(11.34);
Lead->AddNucleus(82,0,0,1.);
Lead->GetNucleus(82,0,0)->SetXSExtension(".50c");
//An other material completely define by hand
Material *B4C=new Material();
B4C->SetDensity(2.52);
B4C->SetDefaultXSExtension(".60c"); //here all extension are set to .60c
B4C->AddNucleus(5,10,0.199);
B4C->AddNucleus(5,11,0.801);
B4C->AddNucleus(6,0,0.25);
//A clone of "static" material: no new MCNP material
Material *B4C_Light=B4C->Clone();
B4C->SetDensity(1.5);
//an evolving material ; automatic extension finding is performed
Material *Comb=new Material();
Comb->SetDensity(10);
Comb->SetEvolution();
Comb->AddNucleus(8,16,2.);
Comb->AddNucleus(92,238,0.95);
Comb->AddNucleus(92,235,0.05);
//a clone of evolving material - here a new MCNP material is created
Material *Comb2=Comb->Clone();
//A clone of "static" material but at a different temperature
Material *B4C_Hot=B4C->Clone(600);
The use of Nucleus::SetXSExtension
or Material::SetDefaultXSExtension
supposed that the user provide a correct xsdir
file with all necessary information.
Here is a short description of the automatic nucleus extension finding.
In order to work, a specific file, BaseSummary.dat, must be
present in the data directory. The aim of this file is to facilitate
the search for a given Z,A,I and related xsdir information
(see also § 1.4.2 and 1.4.3).
Suppose the desierd ZAI exists in the BaseSummary.dat
file. Then the choice of the desired nucleus is based on 2 criteria:
the first one is related to the preference in a nuclear base (ENDB,
JEFF, JENDL) and the version of this base, and the second criterion
is related to the nucleus temperature. A score is calculated for each
criterion, and the best score is chosen. Two classes are in charge
of these criteria: BasePriority and TemperatureMap.
-
-
• BasePriority class: a priority base is organized in 3 levels
(base names) and maximum 3 sub-levels (base versions). Level 1 has
a greater priority than level 2 and so on. By default, the 3 levels
are: (1) ENDFB (USA), (2) JEFF (European) and (3) JENDL (Japan). Only
1 sub-level is defined for each base (6.1 for ENDFB, 3.0 for JEFF
and 3.3 for JENDL). If a user defines for each level the same base
(e.g., (1) ENDFB, (2) ENDB, (3) ENDB), then this imposes the base
choice (i.e., no other choice is possible).
For example
-
- BasePriority *BP=new BasePriority();
BP->SetBasePriority(0,"JEFF"); //1st prefered base
BP->SetVersionPriority(0,"3.1",0); //1st prefered version for 1st prefered base
BP->SetVersionPriority(1,"2.2",0); //2nd prefered version for 1st prefered base
BP->SetBasePriority(1,"ENDFB"); //2nd prefered base
BP->SetBasePriority(2,"JENDL"); //2nd prefered base
gMURE->SetBasePriority (BP);
will choose nuclei first in JEFF 3.1, the if not found, in JEFF 2.2,
then in JEFF (what ever is the version), then in ENDFB (default first
prefered version VI.8) and then in JENDL (default first prefered version
3.3).
If one want to impose nuclei in ENDFB VII.0, then user should do
-
- BasePriority *BP=new BasePriority();
for(int i=0; i<3; i++)
{
-
- BP->SetBasePriority(i,"ENDFB");
for(int j=0; j<3;j++)
-
- BP->SetVersionPriority(j,"7.0",i);
}
gMURE->SetBasePriority (BP);
In that case, only nuclei givent in the wanted nuclear base are used.
-
-
• TemperatureMap class: this class defines a temperature ``binning''
T[i] and a precision ΔT ; an input temperature Tin
can be searched in this binning with respect to the precision. For
example, if
T[0] = 300 K,
T[1] = 500 K and
ΔT = 50 K,
then all Tin in
[250 K, 350 K] will have a score of
![$ {\frac{{\vert T_{in}-T[0]\vert}}{{\Delta T}}}$](img10.gif) ,
all Tin in
[350 K, 450 K] will have a 0 score. The precision
ΔT can be set via gMURE->GetTemperatureMap()->SetDeltaTPrecision().
A zero score in temperature stops the MURE execution: you may either
increase the ΔT precision or build the nucleus data file
(ACE format) at the desired temperature.
,
all Tin in
[350 K, 450 K] will have a 0 score. The precision
ΔT can be set via gMURE->GetTemperatureMap()->SetDeltaTPrecision().
A zero score in temperature stops the MURE execution: you may either
increase the ΔT precision or build the nucleus data file
(ACE format) at the desired temperature.
Using the extension finding, MURE can build the XSDIR
file that is used by MCNP to get the cross-sections used in
the problem. To use this option, you just have to set :
-
- gMURE->SetAutoXSDIR();
When getting the code for MCNP file, MURE will then
save the best line it finds in BaseSummary.dat. Therefore,
right before building the MCNP file (the XSDIR is built
at the first step of an evolution), MURE will build the XSDIR
file by using all these best lines it saved.
IMPORTANT : If an existing XSDIR
is already present in the MCNP run directory, then MURE
will NOT build a new one ; the existing one will be used
by MCNP. Thus either the xsdir is correct, either you
have to remove it.
The MCNPSource
class enables the definition of particle sources (up to now only neutron
sources may be defined). The source may be defined with MCNP
card or as an external source. In the latter case (MCNPSource::SetExtern()),
external source will be read in a special file. This is valid in subcritical
mode as well as in critical (KCODE) mode.
One chooses to run in subcritical mode (default) or in KCODE
mode via the MCNPSource::SetKcode() method.
Once an MCNPSource has been defined, one has to give this source
to MURE class:
-
- MCNPSource *mysource=new MCNPSource(1000); //1000 source particles
gMURE->SetSource(mysource);
To be noticed that, for Kcode, the number of source particles
defined in the constructor of MCNPSource is in fact the number
of neutrons per cycle.
To initiate a KCODE, a SDEF (or KSCR) card is
needed (if no external source is given!). By default, the position
of this initial source is (0,0,0). If you want to change the source
position, use the MCNPSource::SetPosition().
-
- MCNPSource *mysource=new MCNPSource(1000); //1000 source particles/cycle
//Kcode with first expected keff=1, 10 inactive cycles and 80 active ones
mysource->SetKcode(80,10,1);
gMURE->SetSource(mysource);
If one want to use a source from a previous KCODE:
-
- gMURE->UsePreviousRunSource(``olds'');
where the source file olds is the result of a previous run.
In case of evolution, if you do not specify any argument, the source
will be calculated as specified by inactive cycles, and then for next
MCNP runs, the source is taken from the previous cycle.
More elaborated sources
The MCNPSource
gives more details on MCNPSource class possibilities. Two simple
examples are presented:
First
-
- MCNPSource *source=new MCNPSource(1000); //1000 particles per cycle
source->SetKcode(500,20,1); //critical mode (500 active cycles, 2O inactive, supposed keff=1)
source->SetKSRC(); //use fission spectrum for netron energy
source->AddPosition(0,0,0); //add one position for the source at (0,0,0)
source->AddPosition(0.1,0.1,0.1); //add an other one at (10cm,10cm,10cm)
source->AddPosition(0,0,0.2); //add an other one at (0,0,20cm)
source->AddPosition(0,0,-0.2); //add an other one at (0,0,-20cm)
and the second
-
- MCNPSource *source=new MCNPSource(); //SDEF source with 10000 particles
source->SetEnergie("D1"); //energy is define by the source probability 1
source->SetDistribution("RAD=D2 EXT=D3"); // radial and axial extension are
// defined by source information 1 and 2
source->AddBias("SP1 -5 2.0"); //p(E)=E*exp(E/2.MeV)
source->AddBias("SI2 1. 2."); // radial extension from r=1cm to r=2cm
source->AddBias("SI3 -10. 10.");// axial extension from z=-10cm to z=10cm
One can define energy distribution source using the Spectrum
class and the MCNPSource::UseThisEnergyDistribution() method.
Any call to that method will dump in MCNPSource_YourEnergyDistribution.dat,
the ASCII spectrum of this source (for user own use) as well as the
total number of particles emitted (for normalization purpose).
To be noticed: this method
will change the source particle type according to the Spectrum type
(neutrons for NeutronSpectrum,
γ for GammaSpectrum,
...).
This method only change energy distribution of the source
(using MCNP distribution source cards (D, SI, ...) numbered
by default from 800).
It is possible to define volumetric cylindrical sources with the help
of the Tube class. Two methods are available : MCNPSource::AddTubeSource(Tube
* tube, string energy) and MCNPSource::AddTubeSource(Tube
* tube, Spectrum* spectrum). In both cases, the tube is
used to define the shape of the source. The first one allows to use
either mono-energetic sources or using source distributions ``D''
card. In the latter case, the user need to provide himself
the distribution description via the MCNPSource::AddBias()
method (see TubeSource.cxx example). The method using Spectrum
class argument use Spectrum to define both particle
type of the source (neutrons for NeutronSpectrum, γ
for GammaSpectrum, ...) and energy spectrum
(see TubeSource2.cxx example).
Theses 2 methods use internally source distribution cards (D,
SP, SI, ...). The starting number of these distribution is
900. Thus don't use number above 900 to define your own source distribution
and biasing.
Of course you can add more than one Tube source ; but it
is only possible to add more Tube sources with same calling method(either MCNPSource::AddTubeSource(Tube * tube, string energy)
or MCNPSource::AddTubeSource(Tube * tube, Spectrum* spectrum).
One cannot mix them.
If one want to use the energy distribution of a spent fuel which has
cooled for a time t, use MureGui and dump the source
in a MURE format (``Save Data'' button, then select the ``MURE
INPUT Spectrum'' radio widget). The generated file can be inserted
in a MURE ``cxx'' code (c.f. MureGui section 7.3.6).
The Tally
class enables tallies for MCNP to be defined.
WARNING : NEVER USE : ``Tally
*f=new Tally[N]'' BUT USE INSTEAD ``vector<Tally*>
f(N) ; for (int i=0 ; i<N;i++) f[i]=new Tally;''.
The reason is that when tallies are deleted, one need to use either
``delete []'' or ``delete'' ; in MURE, the second case is
chosen which is incompatible with the former declaration.
MCNP tallies are used to store quantities from a run ; there
are 2 main tally types: Surface tallies (type 1 and 2) and Cell tallies
(4,...). At present, only Cell tally of type 1 (current through
a surface), 2 (flux through a surface), 4 (flux in cell), 6 (energy
deposition in a cell) and 7 (fission energy deposition in a cell)
are implemented in MURE. Surface tallies have not been tested at all
and stochastic surface calculation is not implemented in MURE.
A Tally consists of
-
-
• a tally type (what is the desired quantity, e.g. flux in a cell),
-
-
• a list of TallyBin:
this may be SimpleBin (a cell or surface number), GroupBin
(a group of cells or surfaces) or a LatticeBin which allows
to obtain tallies in cells with universes.
-
-
• a Time and/or Energy binning (linear, log or arbitrary binning)
-
-
• a list of TallyFM
(Tally Multiplicator) that allows to obtain cross-sections, .... A
TallyFM is composed of a multiplicative constant, a material
number and a Reaction.
Of course Cell tally bin types could not be mixed with surface tally
bin type. Tally bins are added with the Tally::Add() method
(for cell/surface bins) whereas energy and/or time bins are added
with Tally::AddEnergy() or Tally::AddTime().
Tally multiplicator may be added with Tally::AddMultiplicator()
to obtain cross sections, reaction rates and so on.
Example of Tallies:
-
- Tally *t1=new Tally(); //default tally type is 4: flux in cell
t1->Add(cell_1);
t1->Add(cell_2);
LatticeBin *lpb=new LatticeBin(rod); //rod is a cell associated to an element of a Lattice
lpb1->AddContainer(core); //core is a cell fills by "rods"
t1->Add(lpb);
t1->AddEnergy(1e-2,1.e7); //log energy binning from 0.01 eV to 10 MeV with 10 bin/decade (default)
t1->AddMultiplicator(mat_1,new Reaction(102)); //capture reaction rate
t1->AddMultiplicator(mat_1,-6);//fission reaction rate
When in LatticeBins, you can precise the positions of the cell
in the lattice, use a string which gives the position in the MCNP
way, that is :
-
- string pos="[0 0 0]";
LatticeBin *lpb=new LatticeBin(rod); //rod is a cell associated to an element of a Lattice
lpb->AddContainer(core,pos); //core is a cell fills by "rod" (e.g. a lattice)
This means that you are interested by the flux in the cell rod
which is in the cell core at the lattice position [0,0,0].
The result in MCNP file will be (given that the number of cell
rod is 1 and cell core is 2):
-
- F4:N (1<2 [0 0 0])
Finally, you can use the universe shorthand (u=1 for instance), simply
by giving the universe number, either directly if you know it or by
using Shape::GetUniverse() :
-
- Tally *t1=new Tally();
t1->Add(MainShape->GetUniverse());
Please note that, in MCNP, the universe shorthand doesn't work
for lattice elements filled with the universe number, that is to say,
when a lattice is filled by position, for instance when in MURE
we use Cell::FillLattice(Universe_Number, Position), the universe
is not detected by MCNP. (see example Tally_Test.cxx)
As this shorthand is replaced by all the cells filled with
the universe, we strongly recommend that you use it only if you are
perfectly sure of the number of cells involved in the tally defined
in that way.
Each tally must have a definite volume (or surface). The volume is
set via the Tally::SetBinVolume() or for a given bin, via the
TallyBin::SetBinVolume() or TallyBin::SetVolume(). This
may be done manually or automatically: if no bin volume has been provided,
the volume is automatically calculated by a stochastic method (see
also the note C.1 concerning the volume calculation).
For lattices and universe shorthands, as multiple volumes are needed
for each bin, the SetBinVolume() method precises a partial
number.
-
- Tally *t1=new Tally(4);
t1->Add(Cell1);
t1->SetBinVolume(0,1.e-6,0); // Set the volume of Cell 1 to 1 cm3
LatticeBin *lpb2=new LatticeBin(rod1);
lpb2->AddContainer(rod2);
lpb2->AddContainer(core);
Tally *t2=new Tally(4);
t2->Add(lpb2); // A Lattice Bin giving somthing like (1 2 < 3)
t2->SetBinVolume(0,1.e-6,0); // Set the volume of Cell 1 in cell 3
t2->SetBinVolume(0,1.e-6,1); // Set the volume of Cell 2 in cell 3
The partial number follows the order of the output. (to know exactly
the order for lattice bin volumes, see MCNP doc or example
Tally_test.cxx).
The Tally::AddFluenceToDoseConversion() method converts fluence
(only for F4 type tally) to dose rate (rem/h) using fluence to dose
conversion factors. It can be use only for photons or neutrons. The
conversion factor are store in /path_to_mure/MURE/data/GammaFluenceToDose.dat
and NeutronFluenceToDose.dat (they are taken from [19]).
Interpolation is done for energies and for factors. This interpolation
is done by default in log way. The 2 boolean parameters of Tally::AddFluenceToDoseConversion()
allows to specify linear interpolation for energy (the 1st one) and
conversion factors (the 2nd one).
-
- Tally *MyTally=new Tally(4,ParticleType);//fluence to dose works only for ParticleType=''P'' or ``N''
MyTally->Add(....);
MyTally->AddEnergy(.....);
MyTally->AddFluenceToDoseConversion();
Nuclei Tree
-
-
• To evolve a given material, it is essential to know in advance the
ensemble of nuclei which it can produce via successive nuclear reactions
and decays. This information comes from the Nuclei Tree object,
which is defined by the NucleiTree class, and contains the
linking information between all the nuclei that exist in the chart
of nuclides. Nuclei can be transformed into other nuclei by nuclear
decays (β, α, electron capture, etc.) and nuclear reactions
(
(n, γ), (n, 2n), fission, etc.). In general a particular
nucleus has daughters (those nuclei it can transform into) and parents
(those nuclei that can produce it). To calculate how much of a particular
nucleus is produced during the evolution it is essential to know the
ways in which it can be produced and the ways it can be destroyed.
We cannot only define the total global nuclear tree (the connections
between all 3834 nuclei), but also the local or particular tree for
a given nucleus. The particular tree for a certain nucleus is, in
general, a subset of nuclei and their linking from the global tree.
To extract an individual tree from the global tree, the NucleiTree::ExtractZAI
method is used. The local tree is explored recursively by starting
at the given nucleus (see figure 5.1) and then finding
each successive reaction and decay daughters.
Figure 5.1:
The chart of nuclides used in MURE containing 3834 Nuclei. Nuclei
colored in red are those present in the Nuclear Tree of
232Th.
To build this tree, simple rules are used for determining which reactions
are possible: if Z < 50,
(n, γ) reactions are allowed, if
Z < 90,
(n, γ) and (n, 2n) reactions are allowed, and if
Z≥90,
(n, γ) and (n, 2n) and fission reactions are allowed.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=16cm]{fig/Th232_nocut_initjon}
\par
\end{centering}\par
\protect
\end{figure}](Timg11.gif) |
-
-
• The global nuclear tree has a vector of all the physically possible
ZAI objects, representing the different isotopes, including long-lived
isomers of the same isotope, as an attribute. Each ZAI object contains
vectors of pointers to other ZAI which are either its reaction daughters
or its decay daughters. When a particular tree is extracted, the parental
relations are also determined (see figure 5.2).
It is then possible to follow the tree by jumping from ZAI to ZAI,
and to understand for each ZAI object all the ways it can be created
and destroyed.
Figure 5.2:
The general case of a ZAI object X in a tree with multiple reaction/decay
parents and daughters.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[bb=0bp 0bp 411bp 507bp,clip,width=6cm]{fig/nuclei_tree}
\par
\end{centering}\par
\protect
\end{figure}](Timg12.gif) |
Isotopes in the chart of nuclides have half-lives ranging over ˜40
orders of magnitude. In a reactor core neutron fluxes are much lower
(
∼1015 neutron/cm2/s) than in supernova explosions
(up to
∼1024 neutrons/cm2/s) and thus decay rates
are usually much higher than reactions rates for most short-lived
nuclei. Furthermore, the reactor fuel composition only changes significantly
after some years, so short-lived isotopes play no important role in
the evolution. We can therefore assume that nuclei with short half-lives
decay instantaneously which allows us to simplify the tree and reduce
the number of nuclei in the calculation and hence the calculation
time. To simplify a nuclear tree requires these short-lived nuclei
to be cut out of the tree and their reaction/decay parents and daughters
re-linked into the tree correctly. There are two types of simplification
for a particular tree branch, depending on whether the nucleus X in
question is produced via decay (see figure 5.3)
or nuclear reaction (see figure 5.4) .
Figure 5.3:
Tree simplification if nucleus X is produced via radioactive decay
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=12cm]{fig/nuclei_treeS1}
\par
\end{centering}\par
\protect
\end{figure}](Timg13.gif) |
Note that this means that in some cases a single type of reaction
can produce multiple daughters with different probabilities (branching
ratios), since the reaction daughter had more than one decay daughter
itself, and was cut out of the tree because its half-life was too
short (see figure 5.4). After the simplification
process, these reaction daughters will have weights which are proportional
to the decay branching ratios of the nucleus that was removed from
the tree.
Figure 5.4:
Tree simplification if nucleus X is produced via a reaction. The decay
daughters of X become reaction daughters of A.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=16cm]{fig/nuclei_treeS2}
\par
\end{centering}\par
\protect
\end{figure}](Timg14.gif) |
For a particular tree many nuclei towards the neutron drip-line end
up getting cut out due to their progressively shorter half-lives.
In figure 5.5 we can see the nuclei explored and
then removed from the tree right up to the edge of the nuclear chart.
Figure 5.5:
The simplified nuclear tree for
232Th. Nuclei in yellow
are those which were cut out during the tree exploration process because
their half-lives were too short (less than 1 hour). Nuclei in red
remain in the tree. Reactions follow the same rules that those defined
in fig. 5.1.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/Th232_1h_initjon}
\par
\end{centering}\par
\protect
\end{figure}](Timg15.gif) |
Two nuclei X, and Y will have identical trees if there is a pathway
of decays and reactions that produces Y from X and also a pathway
of decays and/or reactions that produces X from Y. Reactions
(n, γ)
and (n, 2n) move up/down in mass, and decays only move down in mass.
Once the mass is sufficiently low that (n, 2n) reactions are not
permitted, then decays will only take nuclei as far as the valley
of stability and a stable nucleus are reached. At this point the tree
branch ends. However, successive neutron captures are always possible,
therefore fuels containing lighter elements, such as the Oxygen in
Uranium Oxide (UOX) fuel, will have a different tree from a pure fuel's
one such as the 232Th (see figure 5.6).
Figure 5.6:
The UOX tree for
T1/2≥1 hour. Reactions follow the same rules
that those defined in fig. 5.1.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/Uox_1h_initjon}
\par
\end{centering}\par
\protect
\end{figure}](Timg16.gif) |
In all the previous chart figures, the reactions taken into account
are: if Z < 50,
(n, γ), if Z < 90,
(n, γ) and (n, 2n),
and if Z≥90,
(n, γ) and (n, 2n) and fission reactions.
In reality, of course, nuclear cross sections are only available for
a subset of all nuclei. Figures 5.7 and
5.8 show the nuclei with available reaction data found
in the default MCNP4 cross-section (from ENDFB base). All the available
reactions are plotted in figure 5.9.
Figure 5.7:
232Th tree with MCNP default cross-sections and
T1/2≥1
hour.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/Th232_1h_autoreaction}
\par
\end{centering}\par
\protect
\end{figure}](Timg17.gif) |
Figure 5.8:
The UOX tree with MCNP default cross-sections for
T1/2≥1 hour.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/Uox_1h_autoreaction}
\par
\end{centering}\par
\protect
\end{figure}](Timg18.gif) |
Figure 5.9:
MCNP default available reaction data are shown in light blue.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/MCNPreac}
\par
\end{centering}\par
\protect
\end{figure}](Timg19.gif) |
For a realistic half-life cut, the actinide nuclear tree still contains
several hundred nuclei. However, simplification has reduced considerably
the complexity of the problem(see figure 5.10)5.1.
Figure 5.10:
Number of nuclei in the 232Th tree as a function of the minimum
half life allowed,
T1/2min. The blue curve shows the
number of nuclei in the tree if the simple rules for allowed reactions
are used (see figure. 5.1). The black curve shows
the number of nuclei in the tree if allowed reactions are taken from
the MCNP default reaction data base. The green curve corresponds
to the MURE data base built at IPNO/LPSC (not part of the MURE
package). The red dot shows the number of nuclei in the tree for the
default cut (1 hour).
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/NucleivsT1_2}
\par
\end{centering}\par
\protect
\end{figure}](Timg20.gif) |
Fission products are built according to the fission yields available
in nuclear data libraries (ENDF B 6.8). They are the major contributor
to nuclei increased in the reaction tree. Thus, the more FP in nuclear
libraries, the longer the MCNP execution time will be due to
the increase in tally number. Thus, in order to obtain a first approximation,
it may be convenient to run only a selection of fission products that
may be considered as ``fundamental''. We provide a method, NucleiTree::FissionProductSelection()
to choose the most important FP. All other FP will not evolve (no
resolution of Bateman equations) but instead are added in the real
materials of the MCNP file in order to have a good flux description.
A default selection has been entered with the nuclei of Table 5.1
; nevertheless the user can provide a file with its own selection.
To use this selection you must use gMURE->KeepOnlyFissionProductSelection() ;
to give your own selection, use gMURE->KeepOnlyFissionProductSelection(``MyFPSelection.dat'')
where the file MyFPSelection.dat is an ASCII file with each
FP you prefer to keep for evolution : for example
-
- Z1 A1
Z2 A2
...
Table 5.1:
Default 58 fission product selection in NucleiTree::FissionProductSelection().
| 36-Kr- 83 |
46-Pd-107 |
54-Xe-134 |
60-Nd-145 |
62-Sm-152 |
66-Dy-160 |
| 40-Zr- 93 |
46-Pd-108 |
54-Xe-135 |
61-Pm-147 |
63-Eu-151 |
66-Dy-161 |
| 42-Mo- 95 |
47-Ag-109 |
54-Xe-136 |
61-Pm-148 |
63-Eu-152 |
66-Dy-162 |
| 43-Tc- 99 |
48-Cd-113 |
55-Cs-133 |
61-Pm-149 |
63-Eu-153 |
66-Dy-163 |
| 44-Ru-101 |
49-In-115 |
55-Cs-134 |
62-Sm-147 |
63-Eu-154 |
66-Dy-164 |
| 44-Ru-103 |
51-Sb-125 |
55-Cs-137 |
62-Sm-148 |
63-Eu-155 |
67-Ho-165 |
| 44-Ru-106 |
52-Te-127 |
55-Cs-135 |
62-Sm-149 |
64-Gd-155 |
68-Er-166 |
| 45-Rh-103 |
53-I -127 |
56-Ba-138 |
62-Sm-150 |
64-Gd-156 |
68-Er-167 |
| 45-Rh-105 |
53-I -135 |
59-Pr-141 |
62-Sm-151 |
64-Gd-157 |
|
| 46-Pd-105 |
54-Xe-131 |
60-Nd-143 |
64-Gd-154 |
64-Gd-158 |
|
Isomer Production from (n,gamma) or (n,2n) reactions
TO BE NOTICED: Before July
2012, MURE only takes into account the case of 241Am. In the
previous treatment, all ground state production was replaced by 242Cm
; this was of course wrong and lead to an over estimation of 242Cm
production and an under estimation of 242Pu. This has been corrected
since July 2012.
In some cases,
(n, γ) (or (n, 2n)) reactions can lead to
either ground state and isomeric state of a nucleus. For example,
let take the case of 241Am. Neutron capture on this nucleus
leads to
242Am(T1/2∼16h) and
242mAm(141y). Ground
state decays in
242Pu(17.3%) by electronic capture and in
242Cm(82.7%)
by β - decay. A file (IsomerProduction.dat) is provided
to give the branching ratio (for thermal and fast spectrum) to produced
its ground and isomeric states of some nuclei. The format of this
file is
-
- Z A ReactionCode BRth BRf halflife CutFlag
...
where Z, A, ReactionCode, BRth and BRf are respectively the Z (95
for 241Am), A (241 for 241Am), the reaction type (allowed
type are n_gamma or n_2n) and the thermal (87.33%
for 241Am) and fast (85% for 241Am) branching ratio of
the
(n, γ) reaction that leads to ground state (of
242Am). The ``halflife'' parameter is the half life of the
produced ground state (
T1/2∼16h for 242Am) follows
by its unit (here ``h'') ; this parameter in not used,
it is just an indication that can help the user to decide if the last
parameter (CutFlag) is a ``X'' or a ``M''. ``M'' means
that MURE decide what to do according to MURE::GetShortestHalfLife()
method. ``X'' forced the replacement of the ground state
(e.g. 242Am) by its decay daughters. To be noticed, if ``M''
is chosen, wrong results can be obtained in 242Pu and 242Cm
for example, if no cross section is available for the ground state
(242Am).
Evaluated branching ratio data for isomer production can be obtained
at NNDC-ENDF,
in the ``advanced'' or ``extended'' retrieval
tab, by choosing ``n,g'' in the Reaction line and
``MRNP'' (Multiplicities for production of radioactive
elements, MF=9) in the Quantity line. The branching ratio given
in MURE/data/IsomerProduction.dat are effective branching ratio computed
on a typical thermal and fast spectrum as explained in [22]:
BReff = 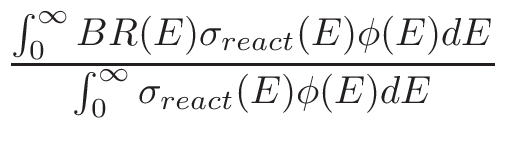
The NNDC-ENDF site gives either the branching ratio
to the ground state or to the isomeric state(s) ; but in MURE
the branching ratio given is always to the ground state.
All provided data files are located in MURE/data. One can use
either, gMURE->SetDATADIR(path) or the environment variable
DATADIR (setenv DATADIR path in csh).
-
-
• When building trees, nuclear mass data are are also incorporated:
the two files used for the input are Mass.dat (a modified version
of the "The 2003 Atomic Mass Evaluation"
data from the National Nuclear Data Center (BNL)) and NaturalIsotopeMass.dat
that is used for non evolving natural isotopes (i.e. with A=0) ;
this file has been built from the NNCD nuclear wallet card. The names
of these files can be defined by gMCNP->SetMassDataFileName()
and gMURE->SetNaturalIsotopeMassFileName() respectively.
-
-
• Decay data: The decay data for the ∼4000 nuclei in the
nuclear chart comes from the chart.JEF3T file which has been
constructed by A. Billebaud and updated by D. Heuer using JEF3T library.
The name of this file is set through the command gMURE->SetNucleiChartFileName().
-
-
• Reaction data: Allowed reactions are defined in ReactionList
class. This class allows different kinds of possibilities for allowed
reaction initialization. The reactions allowed by using the simple
rules (see Fig. 5.1) are defined in ReactionList::InitJon() ;
the automatic detection from available cross-sections is defined in
ReactionList::InitPTO() (see next paragraph for more details).
It uses cross-sections in ACE format. The AvailableReactionChart.dat
helps to save times (this file informs if cross-section are available
or not for each nucleus of chart.JEF3T file). This file could
be made by using MURE/utils/fp/CheckReaction. Other initialization
functions are free to be defined by the user. This is particularly
useful for prohibiting all reactions except a few of particular interest
to the given problem.
One can choose a given method to generate ReactionList with
-
- gMURE->SetReactionListInitMethod(new TSpecificFunctor<ReactionList>(0, &ReactionList::InitMethod));
where InitMethod could be InitJon, InitPTO, ...,
ReactionList::InitPTO() being the default.
-
-
• Isomer production: a file IsomerProduction.dat is provided
in MURE/data that contains information to produce isomer state
and ground state from
(n, γ) reactions. This file contains
Z,A, thermal and fast branching ratio for a mother nucleus (e.g. 241Am)
as well as half-life of the produced ground state (e.g. 242Am)
and a string flag (either ``M'' or ``X'') to know if user want
to replace the ground state by its daughters (e.g. electronic capture
242Pu and β-decay 242Cm daughters).
``M'' means that MURE decide what to do according
to MURE::GetShortestHalfLife() method. ``X'' forced
the replacement of the ground state (e.g. 242Am) by its decay
daughters. If a file IsomerProduction.dat
exists in the local run directory, this file is used instead of the
MURE/data/IsomerProduction.dat one.
-
-
• Fission: Two files are needed for the inclusion of spontaneous
fission decays and neutron induced fission reactions: FPavailable.dat
and FPyield.bin, which have been built by MURE/utils/fp/GenerateFPYield.
The first file is in ASCII format and contains the fission energies
for each available ZAI, and the position (records) of the fission
product yields in the binary file FPyield.bin (see for example
Fig. 5.11 and 5.12).
Even if these files are provided with MURE, you can regenerate them
by providing the appropriate ENDF fission yield file.
Figure 5.11:
Fission yield for 235U.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/U5_nocut_fission}
\par
\end{centering}\par
\protect
\end{figure}](Timg22.gif) |
Figure 5.12:
Fission yield for 235U with T1/2 > 1 hour.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/U5_1h_fission}
\par
\end{centering}\par
\protect
\end{figure}](Timg23.gif) |
Reaction Auto-detection
Reaction auto-detection is based on information found in the MCNP
ACE binary5.2 5.3 format files. Nuclei, for which MCNP reaction cross-section
database information is available, can be found. The auto-detection
process relies on the ReactionList class.
-
-
• First, try to find out if auto-detection has been performed for the
given ZAI by reading the binary file ``ReactionList/Z.bin''
where Z in the proton number of the ZAI. This file contains
an array of Boolean for each reaction.
-
-
• If ZAI is not found in ``ReactionList/Z.bin'', start auto-detection:
-
-
• Try to find in BaseSummary.dat file the ZAI (or an isomeric
state of the ZAI)
-
-
• If it is found, read the ACE file and, among all reactions found in
this file, find those which are significant according to a given threshold
(see next paragraph)
-
-
• Allow significant reactions and disable all others in ReactionList
and add the ZAI to the ``ReactionList/Z.bin'' file with its
reactions.
PLEASE NOTE: if the BaseSummary.dat
file is modified (add new nucleus, or new base) or if the threshold
used to find significant reactions is changed, THEReactionList DIRECTORY MUST
BE REMOVED. Otherwise, your modifications will not be taken into
account.
A quantity Ξi is calculated as
Ξi = 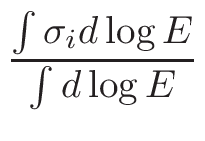
where i stands for reaction i. Then if and only if
Ξi≥σmin
where
σmin is a minimum threshold, the reaction is take
into account ; The default threshold has been set to 0.01 barn5.4. This can be modified by MURE::SetReactionThreshold() called
before any MURE::SetReactionListInitMethod() or Material
definition. In order to save time, the procedure to allow or disable
a reaction for a given nucleus is performed only the first time an
evolution for that nucleus is asked ; then the result for that nucleus
(i.e., a ReactionList object) is stored in a file (one per
Z) in a specific local directory named ReactionList.
Any change of the MURE::SetReactionListInitMethod()or MURE::SetReactionThreshold()after a first run will be taken into account only
if the nucleus has not been already processed: thus you must destroy
the ReactionList directory
in order to have these changes taken into account.
It is possible to put a limit on the recursion depth of the reactions
when calling the NucleiTree::ExtractZAI method. For example
prohibiting 30 or more successive neutron captures limits the nuclei
included in the tree to the top of the actinide region (e.g Fermium,
Californium, etc.) where experimental cross-section information does
not exist, and many successive neutron captures are the only way in
which these nuclei can be produced. The recursion depth parameter
should be used with care. Figure 5.13 shows
the effect of the recursion depth. The default value is 10000...
Figure 5.13:
Effect from limiting the recursion depth for successive reactions
in the 232Th tree, where nuclei with T1/2 < 1 hour have
been removed.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=14cm]{fig/NucleivsRecursion}
\par
\end{centering}\par
\protect
\end{figure}](Timg25.gif) |
Before doing any evolution you must provide a system (geometry based
on Cells, all Materials, running MCNP mode (critical or subcritical),
...). This system definition is normally provided by the MURE
geometry input file (a C++ code). But if you have a very large MCNP
file already defined, it is possible to perform an evolution using
this file without redefining the whole MCNP geometry in MURE
style. The way of doing this is explained in section 6.5.
Simulating time evolution involves solving the well-known Bateman
equations for every given nucleus in every given cell for which evolution
is desired, and carrying out this integration over a discrete number
of time steps. Simulating the fuel burn-up may also involve adjusting
the neutron flux value at every step of the integration process so
as to model constant reactor power, adjusting poison concentration
to keep a given value for keff, ...
The general scheme for the evolution is shown in figure 6.1:
Figure 6.1:
Evolution principle.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/evolution_scheme}
\par
\end{centering}\par
\protect
\end{figure}](Timg26.gif) |
-
-
• The nuclei tree is built once and for all at the first MCNP
run ; it is controled via the Material::SetEvolution() method
which must be called for each evolving Material before
any cell definitions are made. Initial compositions of all materials
are entered by the user and these will evolve automatically.
-
-
• All the necessary tallies for calculating mean neutron fluxes and
cross-sections in evolving cells are automatically built.
-
-
• The MCNP input file with the composition at a given time ti
is built and a MCNP run is performed.
-
-
• Bateman equations are solved for (Runge-Kutta method) using fluxes
and cross-sections of the MCNP run over a given
Δti
-
-
• A new MCNP file with the composition at
ti+1 = ti + Δti
is built, and so on.
At the present time:
-
-
• User must provide all ti in a vector of double where the ith
element is the value of instant ti at which the Monte-Carlo
transport is to be performed.
-
-
• EvolutionControl is used to define evolution conditions (constant
power, keff adjustments, ...). Using inheritance, you may develop
your own EvolutionControl class (see for example the PoisonEvolutionControl
class and § 6.4).
The results of an evolution consist of a number of files stored in
an ``evolution'' directory ; the name of this directory should be
defined by the user via the MURE::SetMCNPRunDirectory function.
Two general sorts of files can be found in this directory : On the
one hand, there are the MCNP input and output files (``o'',
``m'', ``s'' and so on) and on the other, the MURE-generated
summary files (DATA_i, BDATA_i, ...) that can be read by
a ROOT (see ROOT home page)
C++ interface: MureGui.
There are 3 levels of time discretization:
-
-
• The first level is the MCNP step, i.e., the number of
Δti
or MCNP runs. These steps are user-defined and may be unregular.
-
-
• The second level is the discretization within a
Δti. Each
Δti is divided in NRK equally spaced Runge-Kutta
δt steps (which we'll also refer to as RK steps). At each
tk = kδt, Bateman equations are built with given cross-sections.
Special methods controlling the evolution could be called at these
times (e.g. the flux is renormalized to keep the constant power, ...).
-
-
• Then the last discretization step is performed automatically by the
adaptive step size RK method. During this step (discretization of
δt in dtrk) cross-sections as well as fluxes are kept
constant.
Here is the general form of the first-order differential equation
that has to be solved for every nucleus in every evolving cell.
The writing and solving of these equations are systematically carried
out by using internal methods of the EvolutiveSystem class.
Only the general approach will be specified here. This approach involves
the definition of what is called the evolution matrix E
for every evolving cell. The user does not need to know in detail
how it works and it is only being described here for the record.
Internally, every evolving cell knows which nuclei it contains (initially)
or will eventually contain due to the evolution of its initial composition,
thanks to the prior construction of the nuclei tree (c.f. NucleiTree
in chapter 5). The approach taken in MURE
is to assign unique indexes to every nucleus in the cell's composition
so as to build its evolution matrix E. It is a square matrix of
n dimensions, n being the total number of nuclei in the composition
of the cell.
After completion of the matrix, the ith nucleus of a given cell will
evolve according to its own Bateman's equation which will then be
simply written as the sum over all nuclei:
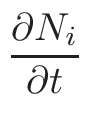 =
= 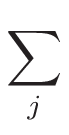 Eij × Nj
Eij × Nj
where Eij is the corresponding element of matrix E
and represents the contribution of the jth nucleus in the cell's composition
to the rate of change in time of the ith nucleus.
The actual writing of the matrix follows the natural structure of
Bateman's equations and is done in two separate parts : first by taking
into account all parent/daughter decay relations between nuclei considering
proper decay branching ratios. After this, the parent/reaction daughters
term is added, where, in the case of fission, fission yields are properly
considered.
The evolution matrix is rebuilt in this way at every Runge-Kutta step
(c.f : Time Discretization) for all evolving cells. The solving for
the material's composition new proportion vector
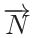 = {N0, N1 ,…, Nn}
is done automatically using a fourth-order Runge-Kutta-type integration
method.
= {N0, N1 ,…, Nn}
is done automatically using a fourth-order Runge-Kutta-type integration
method.
Multi-Threading parallelization
Since gcc version 4.1, OpenMp multi-threading is available
with gcc compilation. Depending on the distribution, libgomp
library (omp.h and libgomp) need to be installed. The
multi-threading behavior is controlled by the OMP_NUM_THREADS
environment variable. Setting it to 1 is equivalent to the single
processor mode. Setting it to the maximum number of cores available,
will run on all that cores (which is the default when this variable
is not set). This variable only controls the behavior of the evolution
NOT the MCNP run itself (which is still controlled by the MURE::SetOMP()
method).
Whereas in general the evolution is useful when the reactor runs at
its given power, it is also possible to introduce some cooling period,
where the power (and thus the flux) is set to 0. This is done by using
an array of booleans of same size than the time vector at which MCNP
runs are normally performed. Each time this array contains a ``true'',
the flux is imposed to 0 for the considered step, else the evolution
is a standard one. The array is passed to MURE via gMURE->SetCooling()
method.
Different way of evolution
We suppose that the evolution is done at a constant power. Evolution
can be performed in different ways that can influence the result.
-
-
• Evolution with a ``constant'' reaction rate: this is the default.
Between 2 MCNP steps, reaction rates are keep ``constant'' ;
a new reaction rate evaluation is performed at the next MCNP
run for the next step. In fact, they are not really constant: due
to renormalization of the flux to keep constant power, reaction rates
used in Bateman equations are in fact,
ασφ where α
is the flux renormalization coefficient. Thus, periodically within
a MCNP step, these reaction rates are readjusted (this explains
the use of the term ``constant'' in quotes). An exampel of such
evolution can be found in MURE/examples/Evolution/EvolvingSphere.cxx.
-
-
• Cross-section evolution: this is no longer the default. Previous MCNP
runs are used to linearly extrapolate the reaction rates for the next
step.
-
-
• Window average evolution: a mean
(σφ) is calculated from
the previous MCNP runs and the actual one ; this mean value is used
to solve Bateman's equations. The window to compute average is based
on MURE::GetFitRangeNumber() previous runs (default
is 4).
-
-
• Predictor-corrector methods. There are 3 Predictor-corrector (PC)
methods implemented. This is actually new and not fully tested (despite
the fact that it currently works). Suppose that the MCNP run
at time TN has been done (leading to reaction rates
(σφ)N).
The evolution has to be performed up to TN+1.
-
-
• PC at middle point: the predictor run is performed with ``constant''
reaction rates
(σφ)N up to
TC =
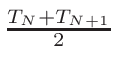 ; then a corrector MCNP run is performed and leads to
(σφ)C.
Starting with the composition of TN, the evolution is done again
from TN to TN+1 with the ``constant'' reaction rates
(σφ)C evaluated at the middle point.
; then a corrector MCNP run is performed and leads to
(σφ)C.
Starting with the composition of TN, the evolution is done again
from TN to TN+1 with the ``constant'' reaction rates
(σφ)C evaluated at the middle point.
-
-
• PC at end-point: the predictor run is performed with ``constant''
reaction rates
(σφ)N up to
TC = TN+1 leading
a composition
CN+1P; then a corrector MCNP run is performed
and leads to
(σφ)N+1. Starting with the composition
of TN, the evolution is done again from TN to TN+1
with the ``constant'' reaction rates
(σφ)N+1 leading
to a composition
CN+1C. Then, the composition used for the
next predictor run (for TN+1 to TN+2) is
CN+1 =
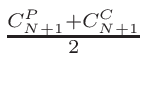 .
.
-
-
• Kind of PC at end-point: the predictor run is done like in b) but
for the corrector run, we used a linear interpolation of reaction
rates from
(σφ)N to
(σφ)N+1. The next
composition for TN+1 to TN+2 is
CN+1 = CN+1C.
First tests seem to give an advantage to method b) for the quality
of its results (compositions, dispersions of composition for M
identical run with different random seeds, ...).
-
-
• Multi-Group evolution[14].
If this method is used, not that reaction rate tallies are not built
in the MCNP input file ; instead, a thin energy binning flux
will be built for each evolving cell. Then, after the MCNP
run, reaction rates are calculated as
 φ(E)σir(E)dE
where the sum is done over each energy group,
σir is
the pointwise cross-section of reaction r for nucleus i read
in the ACE file used for MCNP run (if ASCII version is used,
please note that this will take longer...). The main advantage of
this method is a considerable CPU time saving (more than 30 times
faster6.1 than the ``standard'' evolution). The accuracy of the result are
quite good (˜1% for thermal systems and 5% for fast
ones6.2). To use this method, one has to define ``gMURE->UseMultiGroupTallies();''
at the beginning of the input file (see MURE/examples/Evolution/EvolvingSphere2.cxx
example). The default energy binning for flux is (17900 groups)
φ(E)σir(E)dE
where the sum is done over each energy group,
σir is
the pointwise cross-section of reaction r for nucleus i read
in the ACE file used for MCNP run (if ASCII version is used,
please note that this will take longer...). The main advantage of
this method is a considerable CPU time saving (more than 30 times
faster6.1 than the ``standard'' evolution). The accuracy of the result are
quite good (˜1% for thermal systems and 5% for fast
ones6.2). To use this method, one has to define ``gMURE->UseMultiGroupTallies();''
at the beginning of the input file (see MURE/examples/Evolution/EvolvingSphere2.cxx
example). The default energy binning for flux is (17900 groups)
| Energy range |
10-4eV - 1eV |
1eV - 10eV |
10eV - 10keV |
10keV - 0.1MeV |
0.1MeV - 20MeV |
| Number of bins/decade |
100 |
500 |
5000 |
1000 |
500 |
The main problem of multi-group evolution is the 238U. Its capture
cross section has been chosen to ``optimize'' the group structure
(number of bins/energy interval). In order to take the advantage of
the multi-group CPU time saving, it has been implemented the possibility
to use multi-group runs for all nuclei but 238U : in that case,
the ``standard'' method (real MCNP tally) is used for 238U,
and multi-group tallies for the other nuclei. This is done by setting
the ``StdTallyFor238U'' to ``true'' in the ``MURE::UseMultiGroupTallies()''
method.
Cross-section Evolution
Cross-sections are evolving with time because of the flux shape evolution.
Between 2 MCNP steps, cross-sections are either constant, either evolving.
Taking the cross-section evolution during the ``evolving step''
should enable a better precision and increase evolution step duration,
reducing the CPU time. It is based on linear extrapolation of previous
MCNP runs.
!!!! After a study of error propagation, it
appears that fitting
σφ leads to a bigger dispersion of
cross-section evolution in the result (with a constant power). Thus
this treatment is no more used by default. To use it you must specify
it by a MURE::FitSigmaPhi(true).
The treatment is applied for each cross-section of each nucleus in
each cell. Thus, for the sake of simplicity, we will only consider
a reaction cross-section
σi of a nucleus in a cell.
Since for evolution, reaction rates are used, we should rather consider
the reaction rate
σiφ and not the cross-section
σi.
Suppose that we have performed an evolution up to step k (i.e.,
kth MCNP run is just finished). To know the reaction rate
evolution up to step k + 1 (i.e., just before a new MCNP run),
a linear fit (least square method from Numerical Recipes) is applied
to MURE::GetFitRangeNumber() previous MCNP
reaction rates6.3 (that is to say, MCNP runs k - 3, k - 2, k - 1, and k).
Then, for the evolution over step
k→k + 1, the reaction
rate is extrapolated with
(σiφ)(t) = at + b, where a
and b are the results of the linear regression. Note that for the
first MURE::GetFitRangeNumber() MCNP runs,
reaction rates are kept constant.
As already mentioned, integration of Bateman equations is in fact
done in Nrk Runge-Kutta steps which are automatically divided
in other shorter time steps (adaptive step RK method) ; the reaction
rate evolution is only performed at each RK step level and it is kept
constant within the current RK step. This constant value is evaluated
in the middle of the RK step to be more accurate (see fig. 6.2).
Figure 6.2:
Illustration of a reaction rate evolution. MCNP results are
in black dots. The reaction rate used during the evolution from step
k to step k + 1 is in green whereas the red squares indicate the
time where the extrapolation is performed.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=10cm]{fig/ReactionRate}
\par
\end{centering}\par
\protect
\end{figure}](Timg35.gif) |
In order to better consider the rapid variation of a reaction rate
slope, we have slightly improved the method as follows (here Nfit =MURE::
GetFitRangeNumber()) :
-
-
• a linear regression is performed on Nfit to obtain a' and
b' for the reaction rate evolution
-
-
• a linear regression is performed on Nfit - 1 to obtain a''
and b''
-
-
• then if the 2 slopes a' and a'' are of opposite sign, the slope
taken for the evolution is the mean
a =
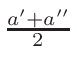 and
b =
and
b = 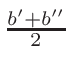
-
-
• or else, a = a' and b = b' if
| a'| < | a''| or a = a''and b = b''
if
| a''| < | a'|
Reactivity Control
NOTE: only few tests have been performed and therfore
many bugs may be present in the Evolution Control.
As already mentioned, the control of the whole evolution is done via
the EvolutionControl class. This class already includes some
useful methods, but the best thing to do in order to implement your
own control is to write a derived class. In a first example, the reactivity
control uses the original EvolutionControl class ; then the
way of implementing your own control will be given.
The example file poison.cxx (MURE/example/poison.cxx)
corresponds to a very simple reactor (cylinder of borated water with
a hexahedral fuel pin lattice). The reactivity control is done by
adjusting the concentration of a poison (the boron) in the water.
We assume that a large reserve of boron is available and thus, when
necessary, we can adjust the boron concentration at a desired value.
The method principle is to calculate an estimation of keff using
the reaction rate extrapolations:
keff = 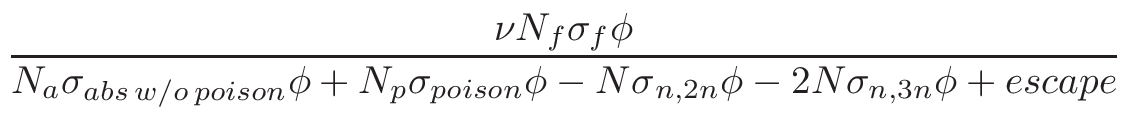
(n,xn), ``escape'' and
σpoison are supposed to be constant
between 2 MCNP steps ; the poison concentration Np is
thus determined using the desired keff in the formula.
-
- ControlMaterial *BoratedWtr=new Material (0.7187023, 673);
BoratedWtr->SetDensity(0.719);
BoratedWtr->AddTheControlNucleus(5, 10,0.00012);
BoratedWtr->AddTheControlNucleus(5,11,0.00048);
BoratedWtr->AddNucleus(8,16,0.333);
BoratedWtr->AddNucleus(1,1,0.667, "H2O");
A ControlMaterial is a Material which is used to control
the evolution, and in this case, a poison to control the reactivity.
The 3th an 4th lines informs us that boron 10 (and 11) are the nuclei
used to control the reactivity. See the ``poison.cxx'' example.
This material must not be an evolving material, because
we'll consider that we can adjust boron concentration every time .
In the keff formula, neutron leakage is needed ; in order to
calculate these escapes, one has to define a F2 tally (flux through
surface) through the most outer Shape of the geometry ; in the example
this leads to:
-
- gMURE->SetOutermostShape(Vessel);
because ``Vessel'' is the outer cylinder of this ``reactor''.
You have to declare the Evolution Control object:
-
- PoisonEvolutionControl *ECon=new PoisonEvolutionControl();
ECon->AddReactions(BoratedWtr);
gMURE->SetEvolutionControl(ECon);
The 2nd line gives the specific EvolutionControl command to
add the required reactions useful for the control (poison absorption,
...)
The aim of this section is to help user implement its own EvolutionControl
using inheritance mechanism. Then you will be able to write your own
specific methods that will be called for the evolution control. Supposed
we wish to create a MyEvolutionControl class: the hxx
and cxx files are in MURE/example/.
NOTE: Don't forget to redefine the EvolutionControl*
Clone() as:
-
- EvolutionControl* Clone(){return new MyEvolutionControl(*this);}
Each method and variable of EvolutionControl are known in MyEvolutionControl
; but because of the virtuality of some methods, the ControlAtEachMCNPStep(),
ControlAtEachRKStep() and ControlAfterEndOfRKIntegration()
methods of MyEvolutionControl will be called instead of the
ones of EvolutionControl. This means that these original methods
of EvolutionControl are no more called, and
thus you have to read them carefully to implement what is needed or
necessary for your evolution control.
Now to use this new class in Myprog.cxx:
-
- #include <iostream>
#include <cmath>
using namespace std;
#include "MureHeaders.hxx"
#include "MyEvolutionControl.hxx"
...
int main(int argc, char** argv)
{
...
MyEvolutionControl *NewEC=new MyEvolutionControl();
gMURE->SetEvolutionControl(NewEC);
}
and to compile the Makefile for the compilation will be
-
- g++ -g -O -Wall -fPIC -I../../source/include -I../../source/external -c MyEvolutionControl.cxx
g++ -g -O -o Myprog Myprog.cxx MyEvolutionControl.o -I../../source/include -I../../source/external/\
-L../../lib -lMUREpkg -lvalerr -lmctal
Evolution of a MCNP user defined geometry
This section is devoted to users who have already defined a complex
MCNP file and would rather not use the MURE geometry
capability when making evolution. Even if this task requires some
work, the procedure is simple. User has to redefine in MURE
style, ALL materials of its geometry and
all EVOLVING cells (but not the shapes associated
to the cells). Of course, user will need all files required by a standard
evolution (BaseSummary.dat, AvailableReactionChart.dat,
...)
The principle is the following: a line by line of a MCNP
user input file are copied, but
-
-
• if the cell number found corresponds to one of the ``virtual'' evolving
cells defined, then the density of the evolving material at the given
evolution step is taken into account. Be sure that 2 evolving cells
must have 2 different materials (because they usually evolve differently
even if at the beginning they are the same) ; thus, it is at present
not possible to make the evolution of a cell defined by ``like
but'' because there is no material on this cell line.
-
-
• The general MCNP block will be read, but all the material description
(``M'' and ``MT'' cards) will be skipped and replaced by the MURE
material definition. Note that if one wishes to use source MURE
definitions, particle MODE definitions or PRDMP MURE definitions,
any ``SDEF'', ``KSRC'', and ``KCODE'' (for source) or ``MODE''
or ``PRDMP'' must be removed from the original file. If you have
defined tallies, they will be copied (line by line) and the necessary
tallies for evolution will be constructed starting from your highest
tally number : for example, if you defined 2 tallies F34 and F44,
the automatic tallies for evolution will start at F54 ; tally numbers
4,14 and 24, are not used.
For material declaration, you must use the special Material
constructor that takes as a single argument the material number ;
this number is the one you have written in the MCNP input file. Don't
forget to declare ALL materials of the geometry (evolving or non evolving).
For non evolving materials, you must ask MURE
to include them in the MCNP
output file by using Material::AddToGlobalNucleiVector()
after the last input nucleus.
For cell declaration, you must use the special Cell
constructor ; it takes the cell number (the one you have written in
the MCNP input file), an evolving Material pointer and
the cell volume (in m3). ONLY evolving cells should
be declared.
The Original MCNP input name is defined by MURE::SetUserGeometryInputFile()
method. You can also defined all desired cards of the general data
block (source, physical card, ...). The rest of the evolution is completely
analog to what is explained in the above sections. Don't forget to
provide a mean to calculate the tally normalization factor (you may
either give a predefined power or use the MURE::SetTallyNormalizationFactor()).
An example is shown in UserGeo.cxx with the UserMCNPGeo
MCNP input file.
Sometimes, the evolution is performed with power variations, some
parameters such as boron concentration, temperature, ... are changing.
This can be achieve through the EvolutionWrapper class (see
EvolutionWrapper
class) . Such conditions are illustrated on the following example:
-
- EvolutionWrapper *EC=new EvolutionWrapper(); // create EvolutionWrapper
EC->AddPhase(100,3,1); // create a new 100 days phase with three MCNP steps, (1=logarithmic discretization)
EC->SetPowerLinear(0,4e4); // raise power from 0 to 40 kW
EC->SetMaterialBoronLinear(Cell_of_BoratedWater->GetMaterial(),1000e-6,500e-6); //boron depletion from 1000 to 500 ppm
EC->AddPhase(100,1,0); // a new single-step 100 days cooling phase
EC->SetPowerCooling();
EC->AddPhase(100,3,0); // a new 100 days phase with three equal(0=linear discretization) MCNP steps
EC->SetPowerConstant(4e4); // power is kept constant at 40kW in that phase
EC->Evolve(); // run the evolution (DO NOT CALL the MURE:Evolution method ; it is done here)
Equilibrium of Xe-135
In some circumstances, flux oscillations in weak coupled systems creates
numerical (unphysical) Xe oscillations. These Xe oscillations enhanced
the flux oscillations causing numerical instabilities. To reduce these
instabilities, a special treatment has been implemented. To use this
treatment, one has to call the MURE::SetXe135Equilibrium(double
teq) method, where teq is the time from which the treatment
is really applied (default time value is
3×T1/2135Xe∼27h).
Here is the description of what is done:
-
-
• if t < teq, then the standard evolution is carried out (i.e. no
special treatment)
-
-
• if
t≥teq, then
-
-
• the 135Xe Bateman equation is imposed to be at equilibrium :
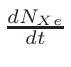 = 0
= 0
-
-
• the 135Xe is calculated as
NXe = 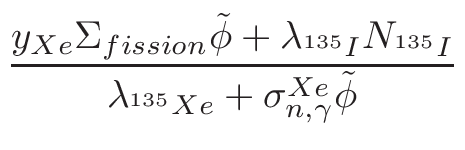
|
(6.1) |
where yXe is the fission yield for 135Xe,
Σfission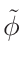 is the number of fissions,
λi is the decay constant for
nuclei i and
is the number of fissions,
λi is the decay constant for
nuclei i and
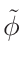 is a ``mean'' flux in the cell calculated
as
is a ``mean'' flux in the cell calculated
as
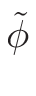 =
= 
if there is a factor greater than 1.5 between
φprevious MCNP run
and
φcurrent MCNP run, else
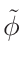 = φcurrent MCNP run
= φcurrent MCNP run
-
-
• the 135I used in (6.1) is calculated in the same way
:
NI = 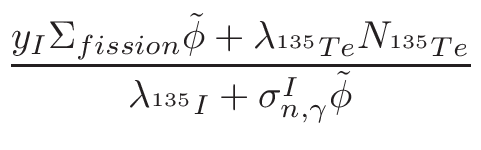
but this value is only used in for the (6.1). To be noticed,
that in general, due to its very short period (
T1/2∼19s),
the 135Te is absent of the evolution ; it is then taken into
account in the iodine fission yield yI as explained in the Nuclei
Tree section (c.f. 5).
At present, results from the evolution are stored in the MCNP
Run directory. There are 4 types of MURE files generated in
addition to the MCNP files for each evolution step:
-
-
• DATA_xxx files are written for each step number xxx,
and contain not only the Material composition information, but also
average cross-sections for every possible reactions for all evolving
cells in the geometry. In addition, average flux for each cell, cell
spatial variables (if defined), keff, and time are also written
out. They are written just before RK steps ONLY IF MURE:SetWriteASCIIData()
has been called.
-
-
• BDATA_xxx files contain the same information as the
above files but in binary format. Initially it was expected that these
files would be much shorter in length than the ASCII files, but it
appears that not much space is saved if binary files are used to store
MURE results. Nevertheless it is much faster to use these files
for post-treatment. They are written just before RK steps by default.
On can disable this writing by using MURE::SetWriteBinaryData(false).
-
-
• KDATA contains all the keff information (with
statistical errors) for all evolution steps in one file. These data
are also contained in [B]DATA_xxx.
-
-
• FDATA contains all the data pertaining to the fission
rates of various nuclei. For all the 50 or so nuclei which can fission,
the rate (in fissions per second) integrated over all the evolving
cells, is written out.
When using reprocessing feature DATA_bxxx or/and
BDATA_bxxx files are also written just at the end
of RK steps. When using PoisonEvolutionControl, additional
files are also written such as POISON_PROPS which contains
the poison proportion as a function of time.
This graphical interface is now deprecated.
Except for ExamTree.tcl
-
-
• ExamTree.tcl
To run these scripts from anywhere it is a good idea to add the TclScripts
directory to your path. You must also set the DATADIRenvironment variable.
-
-
• The ExamTree.tcl script is useful for exploring the
evolution nuclear tree, which can be written out for the global nuclei
vector of the MURE class using gMURE->WriteAsciiTree(``myfile.dat'');
or the tree for a material object Material->DumpTree(``myfile.dat'');
To explore the tree, type
ExamTree.tcl myfile.dat
Everything else is intuitive and self-explanatory. Just click either
on the nuclear chart, or the Nucleus X window.
Reading the data files with ROOT graphical interface
This is a C++ GUI base on ROOT. Thus, before using this GUI,
you must install a recent ROOT version (5.0 or any later
version). This is easy because binary files can be downloaded from
the ROOT home page (http://root.cern.ch).
We have chosen ROOT because:
-
-
• it provides a large number of widgets
-
-
• it is a very simple way of modifying, saving graphs: zoom on axis,
grid, log scale, changing font, color, text position and so on as
well as various picture saving formats are available (eps, jpeg, png,
gif, ...).
The GUI is in MURE/gui ; to build this GUI, a simple ``make''
in this directory will do the job. The install.sh script should have
set the flags according to your ROOT installation7.1 and check if Lapack package is avilable. LAPACK is a Linear
Algebra PACKage use to solve the set of coupled differential equations
for decays by a matrix diagonalization procedure. If this package
is not installed, you have to install it (see § 1.4.4)
to run the radiotoxicity module (but all other MureGui
capabilities can run without Lapack). A simple ``make''
will build the MureGui executable:
-
- MureGui [-type c -dataname str] DirName1 [DirName2 ...]
where
-
-
• DirName1 is the MURE evolution directory (containing the BDATA_*
or DATA_* files) and optional DirName2, ... are other directories
to compare evolutions. The line style of plotted graphs is different
for each directory (solid=DirName1, dash=DirName2, dot=DirName3, dash_dot=DirName4,
...). NOTE: when comparing evolutions, you must be sure that the cell
composition of the different evolutions are the same: the list of
non empty proportion nucleus must be in the same order.
-
-
• Optional -type follows by a character which is either ``A''
(or ``a'') or ``B'' (or ``b'') ; ``A'' is to read DATA_*
files (i.e. ASCII files) and ``B'' is to read BDATA_* files.
The latter is the default (it is faster to read and a bit smaller)
; the ASCII files may be read when binary formats are not recognized
(big endian->little endian, ...)
-
-
• Optional -dataname follows by a string which is the data evolution
prefix file name ; default is BDATA_* for binary reading and DATA_*
for ASCII reading7.2.
A module in the transport code DRAGON has been developed to copy the
results in DATA ASCII file format.
The interface has a Main windows composed of 8 tabs (Inventories,
Cross-sections, Fluxes, Reaction Rates, K_effective,
Breeding Ratio, Radiotoxicity and Spatial Variables,
see Fig. 7.1) and can have up to 8 plot
windows (one for each tab).
Whereas MureGui is graphical interface, the ``Terminal''
window used to run this program is often used for some important warnings/information/output:
don't forget to look at it!
-
-
• In the Inventory Tab, colors of nuclei (see Fig. 7.1)
correspond to the total mass scale importance (red: large mass->black:
small mass). Nuclei are sorted in 4 categories (Actinides, Fission
Products, Gas, and Miscellaneous) but a nucleus could belong to more
than one category (a gaseous fission product is in FP and in Gas).
``FP'' and ``AM'' check boxes allows respectively the plotting
of total fission products and total minor actinides (Np and Am, Cm,
...) . The total mass of checked nuclei can also be automatically
performed using the ``Sum of Selected'' check boxes7.3. Finally, nuclei inventories are given in ``g'' or ``Mol''. When
several physical cells i are selected (see later with Spatial Variable
combo box), the total inventory of one nucleus is simply given by
the sum of inventories in each region. Thus we have:
Ntot =  Ni
Ni
Figure 7.1:
MureGui main window. Inventory Tab.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[clip,width=14cm]{fig/MureGui}
\par
\end{centering}\par
\protect
\end{figure}](Timg46.gif) |
-
-
• In the Cross-section Tab, colors only help users to see the
isotopes (all reactions for a same isotope are on the same color).
The ``FP''' check box allows the plotting of the mean fission products
total cross-section. Similarly with the Inventory tab, the total cross-section
can be obtained with the ``Sum of Selected'' check box (but
FP and AM check boxes are not taken into account in the sum). Microscopic
and macroscopic cross-sections are available. When several physical
cells i are selected (see later with Spatial Variable combo box),
an equivalent cross-section
 is computed for all
reactions to maintain their total reaction rate:
is computed for all
reactions to maintain their total reaction rate:
 =
= 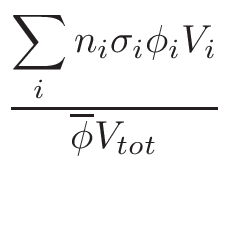
where the nuclei density is
ni = 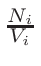 , the mean
flux is
, the mean
flux is
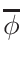 =
= 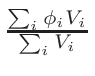 and the total volume of all cells is
Vtot =
and the total volume of all cells is
Vtot = 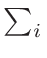 Vi. The
numerator is the total number of reactions in all i-cells. Thus,
one can define an equivalent microscopic cross-section:
Vi. The
numerator is the total number of reactions in all i-cells. Thus,
one can define an equivalent microscopic cross-section:
Note:
-
-
• when the density of one nuclei is null, a very small and uniform density
is used to compute the equivalent microscopic cross-section (
n = 10-20at.cm-3).
-
-
• This mean cross-section is useful to compute ``simplified''
Batemann equations. But one has to be very attentive to its physical
signification when lot of cells with different fluxes and concentrations
are involved ; then this mean value may be greater than all individual
cross-section of each cell due to an under estimation of the denominator.
-
-
• Sometimes, it may be useful to compute the mean microscopic cross-section
over the spectrum:
〈σ〉 = 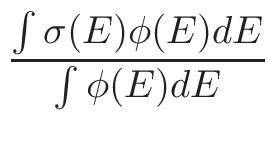
Then one can compute a average cross-section over the cells as
〈σ〉 = 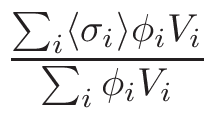 .
In MureGui, one can plot this king of microscopic cross-section by
selecting the ``Micro (spectrum)'' radio widget.
.
In MureGui, one can plot this king of microscopic cross-section by
selecting the ``Micro (spectrum)'' radio widget.
-
-
• In the Flux Tab, the ``All cell'' and ``Sum
of Selected'' check boxes allow users to plot a mean flux over all
or selected evolving cells i. The mean flux is given by:
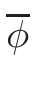 =
= 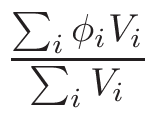
-
-
• In the Reaction Rate Tab, the ``FP'' and ``Sum of Selected''
check boxes allow users to plot total reaction rate of fission products
and the sum of selected reaction rates respectively. The generated
power can also be obtained using the ``Power'' check box.
Power results are returned in the terminal when the graph
is refreshed. The ``(Un)Select Fissil'' button selects (or
unselects) all available fission reactions automatically. Note that
released energy per fission values (Q_values) are automatically selected
according to the transport code previously used (DRAGON or MCNP).
In this Tab, it is also possible to plot Neutron Balance normalized
per 1000 fissions. Once the user has selected the wanted reaction
rates (or all reaction rates for the fissile (``(Un)Select
Fissile'' button) or for all nuclei (``(Un)Select All'' button),
the neutron balance is plotted using histogram bars. The box ``Threshold
to Others'' allow user to group all reaction rates less than the
threshold (default 0.1 per mil) in a category named ``Others'' (see
fig. 7.2 and fig 7.3).
The ``Dir'' number is the number of the Dirname argument of MureGui
and the number following the ``@'' character corresponds to the
time at which the MCNP run is done (thus figure 7.2
corresponds to first Dirname at time t=1004.44 days where a MCNP run
was performed)
Figure 7.2:
Neutron Balance window. In this example, the reaction rates less than
3 per mil are grouped in the ``Others'' category.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/NeutronBalanceWin}
\par
\end{centering}\par
\protect
\par
\end{figure}](Timg62.gif) |
Figure 7.3:
Neutron balance plot.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=14cm]{fig/NeutronBalance}\protect
\par
\end{centering}\par
\end{figure}](Timg63.gif) |
-
-
• In the Keff Tab, the ``Keff'' check box allows user
to plot the multiplication factor keff of the assembly with
evolution time. The ``Average Keff'' check box computes and
plots the average neutron multiplication factor
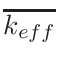 of an assembly along its life. It is particularly useful in CANDU
reactors at the refueling equilibrium state. The average value
of an assembly along its life. It is particularly useful in CANDU
reactors at the refueling equilibrium state. The average value
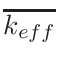 is given by:
is given by:
-
-
• In the Breeding Ratio Tab, users have to select some nuclei
among all heavy elements in order to define them as fissile for the
calculation of Breeding Ratio (BR) and Fissile Inventory Ratio (FIR).
The (instantaneous) BR is computed at a given time t as the ratio
of the total production rate of the so-defined fissile nuclei at time
t over the total disappearance rate of the same nuclei at the same
time. Up to now, only fissile nuclei among 233U, 235U,
239Pu and 241Pu can be defined as fissile and taken into
account for BR calculation, with a special treatment for 233U
(which production rate is 233Pa decay rate) and 241Pu
(which disappearance rate includes its decay rate).
The FIR is computed as the ratio of fissile nuclei between actual
and initial time :
FIR = 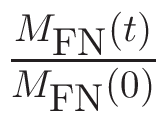
Note that if the initial fissile nuclei mass is 0, no plot is returned.
In the case of 233U selected as fissile, selecting 233Pa
as fissile too gives access to the effective FIR values, with each
calculation time as a possible End Of Cycle. Indeed this accounts
for 233Pa out-of-flux decay, producing 233U without loss.
In this case, a warning is printed to inform the user that 233Pa
is used this way only for FIR (BR is still computed without Pa-233
defined as fissile, and using its decay rate as 233U production
rate).
-
-
• In the Radiotoxicity Tab (see also section 7.3.6),
shown in Fig. 7.4, (only
if Lapack library has been used), decay calculations can be performed
for the final inventory after an evolution has been done. Determination
of total and partial radiotoxocities, heat released and activities
as a function of time can be computed for a given system. Note that
if, for radiotoxicity post-treatment, MureGui is used from
in a directory where the MURE ``data'' directory is not present
just above the current path, you must define the DATADIR
variable.
Figure 7.4:
MureGui : the radiotoxicity Tab.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=14cm]{fig/radiotox_GUI}
\par
\end{centering}\par
\protect
\end{figure}](Timg69.gif) |
-
-
• Users should click on the red ``Build Mat'' button before
taking any further action. This will compute the Material and
the matrices. The material is based on the material defined in the
DATA or BDATA files where all the nuclei are copied, and all their
decay children. NO CUT-OFF is used to select
the children. By default, spontaneous fissions are not taken into
account ; in order to allow it, check the ``with SF'' button
BEFORE clicking the ``Built Mat'' button. The matrices
for decay calculations A are also computed once and for all. The
variation of the isotopic vector N is given by:
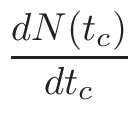 = - A.N(tc)
= - A.N(tc)
where tc represents the cooling time (after irradiation). The
solution of this equation is simply given by:
N(tc) = N(0).exp(- A.tc)
This equation represents a set of coupled differential equations for
the decays which is solved by a matrix diagonalization procedure based
on the LAPACK standard libraries (resolution is performed
at the beginning). Inventory composition over time is then directly
obtained from the initial composition.
-
-
• The ``Nuclei Extraction'' frame allows user to specify what
percentage of nuclei of the current composition is taken into account
for activity, radiotoxicity, ... calculation. When one choose ``Partial
fuel extraction'' a new window appears to choose the per cent of
category you keep: 100% means that all that category is kept. For
example, putting 100% for all categories except 1% for U and Pu
mean that the radiotoxicity is calculated for the initial composition
where only 1% of the U and Pu nuclei are kept, all other nuclei being
completely taken into account. User can choose a cooling time before
the extraction occurs. In that case, the plot window will start for
t = 0 after the core discharge to the cooling time value7.4 ; then, the partial extraction is done and the result is plotted.
A dash red line is drawn to show the time of extraction. A ``Chars''
logo button allows user to plot energy spectra of
γ, β, α
and neutron emission of ``spent fuel'' (see section 7.3.6).
-
-
• In the ``Miscellaneous'' frame, one can also select the value
to be plotted: ``Activity'', ``Radiotoxicity'', ``Heat'' released
and ``Inventory''. By selecting the ``By mother'' check
button, the radiotoxicity is computed by mother nucleus (i.e. present
at the starting time) in order to see the contribution to the activity
of a given nuclei (the daughters of this nucleus are part of its activity).
Note, the ``By mother'' calculation takes much
more cpu time! ''FP'', ``MA'' and ``Total'' check boxes allow
one to plot the total value for fission products, minor actinides,
and all nuclei respectively. A combo box can be used to plot ``selected''
nuclei, ``selected nuclei & their sum'' or ``only the sum'' of
selected nuclei (FP and MA check boxes are not taken into account
in the sum).
-
-
• In the ``Irradiation'' frame, see Fig 7.5,
one can choose the burnup of the spent fuel (i.e., the MCNP
step given at a time). The ``Dir # num'' allows to choose which
evolution directory to consider in the case or more than one evolution
directory is given to MurGui arguments. The evolution (cooling)
of the spent fuel is specified by the evolution parameter: the cooling
starts at t = 0, but the plot start at the first value of the ``Evolution
Period'' frame ; the final time, number of time-steps and whether
the steps are logarithmic or linear are then given. Note that the
graph are on a log scale, thus, initial time has to be strictly positive
(minimum value is 1 minute). The number of steps does not affect the
results, but only the smoothness of the curve.
Figure 7.5:
``Irradiation'' frame. Here, the first Dirname at time t=0, i.e.,
the first MCNP step, is used. The fuel cooling will be plotted from
1 year to 100 million of years with 50 log steps.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/radiotox_Irrad}
\par
\end{centering}\par
\protect
\end{figure}](Timg71.gif) |
-
-
• The ``Spatial Var'' tab allows the plotting of spatial flux
(or power deposit) dependence if you have defined spatial variables
(see the Cell class and next paragraph). It
is present only if Spatial varaibles have been defined. The ``Plotting
Time'' frame allows user to select the time at which the plot is
done. The ``Variable choice'' frame allows user to select
what to plot (in the ``Plotting Variable'' combo box) and
with, eventually, a condition on spatial variables (``Conditional
Variable'' combo box). For example, if a core has been divided in
N radial zone and M axial zone, you can plot the mean flux as a function
of Z for every radial zone (see figure 7.6).
One can also plot this flux but only for a given radial zone by selecting
the desired ``ring'' in the ``Conditional Variable'' combo box.
The ``Same Plot'' check button, allow users to overlap plots.
Figure 7.6:
Spatial Var Tab - This will plot the flux as a function of Z for t = 0
whatever the spatial variables (no condition).
![\begin{figure}\endgraf
\par
\begin{centering}
\includegraphics[width=14cm]{fig/spatialvar_tab}
\par
\end{centering}\par
\protect
\par
\end{figure}](Timg72.gif) |
It is possible to evaluate the time evolution of radiotoxicity (or
activity, ...) of an user input composition without making any MURE/MCNP
evolution. This is of course an out flux evolution (only decays are
taken into account). User should create a file name DATA_000 in a
given directory (let say ``TestDir''). This file must contain
-
- V -1
UNIT
n
Z1 A1 I1 M1 P1
Z2 A2 I2 M2 P2
...
Zn An In Mn Pn
where UNIT is a string among ``At'', ``Mol'', ``Wgt(g)'', ``Wgt(kg)'',
``Wgt(t)'' giving the unit of each ``proportion Pi'' ; ``n''
is the number of different isotopes (Zi,Ai,Ii) and ``Mi'' is the
molar mass of the isotope. For example, to see the evolution of 2.975
kg of 238U the DATA_000 file is
-
- V -1
Wgt(kg)
1
92 238 0 238.05 2.975
Then launch MureGui as :
-
- MureGui -type a TestDir
and go in the ``Radiotoxicity'' tab ; this gives a total radiotoxicity
of about 1mCi for 238U at t = 0 ; then it reaches the secular
equilibrium after 2 million years to
14×1mCi (13 radioactive
daughters of 238U+238U).
Users can define Spatial variables for cells (see the Cell
class). The aim of these variables is only to extract results in a
simpler way (this means that you can add spatial variables after the
evolution is done and redo the evolution keeping MCNP files without
any problems). If such variables have been defined you can plot quantities
according to spatial variables.
Suppose we have done the evolution of 3 rings of a cylindrical core
divided in 3 parts along the cylinder axis. If, for each of these
9 evolving cells, 2 spatial variables named ``R'' and ``Z'' with
value corresponding to the typical cell locations have been defined,
then the combo box of the ``Cell Spatial Var'' will allow users
to plot for example 235U quantity for all cells with a particular
radius Ri (i.e. whatever other Z value, see Fig 7.7)
or to plot this quantity only for a given Ri and Zi (see
Fig 7.8)
Figure 7.7:
MureGui - Spatial Variable combo box selected for all cells of R = 1.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/spatialvarR1}
\par
\end{centering}\par
\protect
\end{figure}](Timg73.gif) |
Figure 7.8:
MureGui - Spatial Variable combo box selected for the cell located
at R = 1 and Z = 0.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/spatialvarR1Z0}
\par
\end{centering}\par
\protect
\end{figure}](Timg74.gif) |
A linear interpolation is performed on the plotted data for
the selected Tab at the corresponding time (and not the selected data
of this Tab). Results are returned in the terminal. Note that no time
unit is specified, thus it must be coherent with the plotted data.
Figure 7.9:
MureGui - Interpolation and Error Bars.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=8cm]{fig/MureGui-Interpolation}
\par
\end{centering}\par
\protect
\end{figure}](Timg75.gif) |
When statistical errors are available, error bars may be added to
the corresponding graphs. Note that MCNP provides errors on fluxes,
reaction rates and keff values. Thus, the Error Bars Button
has no effect on the Inventory and Conversion Rate tabs.
In [B]DATA_xxx files, are written keff, fluxes
(with their MCNP absolute error), compositions of each nuclei (in
atoms), and cross-sections with their error. This error is not really
correct because it has been calculated as
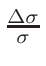 =
= 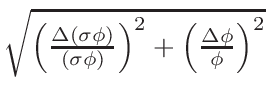 . This is correct only if φ and
(σφ) are not correlated...which
is obviously not the case. Thus only error for keff and fluxes
are really correct.
. This is correct only if φ and
(σφ) are not correlated...which
is obviously not the case. Thus only error for keff and fluxes
are really correct.
For the average flux
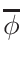 on several individual cells
(with an individual flux of φi), we have:
on several individual cells
(with an individual flux of φi), we have:
If the sum of cross-sections is computed, the associated errors is
given by:
For the average reaction rate
Nj, tot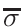
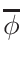 of one specific reaction j (linked to the corresponding nucleus)
on several individual cells i, we have:
of one specific reaction j (linked to the corresponding nucleus)
on several individual cells i, we have:
For the error associated with the power computation, we can used similar
formula as for reaction rates, i.e.:
Δ(
 Pj
Pj) =
![$ \sqrt{{\sum_{j}\sum_{i}\left(Q_{j}N_{j,i}\sigma{}_{j,i}\phi_{i}\right)^{2}\lef...
...gma_{j,i}}\right)^{2}+\left(\frac{\Delta\phi_{i}}{\phi_{i}}\right)^{2}\right]}}$](img89.gif)
-
-
• ``Plot (All)'' button: Except for the ``Cell Spatial
Var'' frame in the main window where by selecting a variable, the
plot is automatically done, you must push the ``Plot(All)''
button to plot a graph ; The plot window is selected according to
the Tab in the main window.
-
-
• ``Save Data'' button: This button is used to save plotted
graph data from the selected plot window in an ASCII file.
-
-
• ``Exec Macro'' button: This button is used to apply a ROOT/C++
interpreted (no compilation required) function to selected plot window.
See for instance the MyMacro.cxx example in the MURE/gui
directory. To use this macro (which does a linear fit of the ith graph),
just click on the ``Exec Macro'' button and type MyMacro.cxx(i)
where i is the number of the graph desired.
More about Radiotoxicity Tab
It is possible to obtain activity, inventory, heat of a user input
mixture composed of n nuclei as a function of time in a ``cooling''
phase (i.e. outside of a flux) in a very easy way. User has to create
a directory (let's call it ``tox'') containing a file named
DATA_000. This file has the following form:
-
- V -1
units
n
Z0 A0 I0 M0 X0
Z0 A0 I0 M0 X0
...
Zn An In Mn Xn
where units is one of ``At'', ``Mol'', ``Wgt(g)'',
``Wgt(kg)'' or ``Wgt(t)'' (At=atomes, Mol=moles,
Wgt(g)= mass in g, Wgt(kg)= mass in kg
and Wgt(t)=mass in metric tons) that corresponds to the unit
of the Xi values input for each nuclei defined by its Zi
(proton number), Ai (atomic number), Ii (isomeric state,
0 for ground state, 1 for 1st isomeric state, ...). Mi is the
molar mass in g/mol of the ith nuclei. For example, one can
see how
2.975 kg of 238U reaches the secular equilibrium
with
-
- V -1
Wgt(kg)
1
92 238 0 238.05 2.975
This file is saved in the tox/DATA_000. The activity of this
initial composition is obtained by doing
-
- MureGui -type a tox
One can see that the activity starts from 1 mCi and reaches secular
equilibrium (14 mCi) after
∼2×106 years.
-
-
• The ``type -a'' is necessary because the DATA_000
file is in ASCII and not in binary (the default of MureGui)
-
-
• Depending on your installation, you probably need to set the environment
variable DATADIR to the correct path (for example in csh,
setenv DATADIR /MURE_install_path/MURE/data)
User can plot spectra of an evolving material. This feature is ``hidden''
in the Radiotoxicity Tab : press the ``CHARS logo'' or depending
on your installation, the small down arrow, between ``Irradiation''
and ``Cell Spatial Var'' to make it appear (fig. 7.10)
.
Figure 7.10:
MureGui Radiotoxixity Tab
![\begin{figure}\endgraf
\centering {}\includegraphics[clip,width=15cm]{fig/GuiRadioTab}\protect
\end{figure}](Timg90.gif) |
First of all, spectra has to be built pressing the ``Build Spectra''
button. It will create a γ spectra for the ``Gamma Spectrum''
tab,
β, α and neutron spectra in the corresponding tabs
for each nucleus. This step could take a while especially for the
Gammas. In the ``Gamma Spectrum'' tab (see fig. 7.10),
gammas produced by decay modes selected in the ``Decay Mode'' from
are plotted.
This frame is used to plot either 3D spectra (activity versus energy
and time) for
γ, β, α and neutrons or ``time slice
cuts'' using the ``2D slice'' slider of these spectra. For 3D spectra,
only one nucleus (or one group among ``total'', ``FP'' or ``MA'')
can be plotted.
This frame (only for gammas and alphas) allows user to find the emitter
of rays of energy
E±ΔE enters in combo boxes (E and
ΔE are both in keV, see fig. 7.11).
Figure 7.11:
Find gamma emitters at
185keV±1keV. They are sorted by decreasing
intensity (gamma intensity×atoms) and the decay mode is indicated
(alpha, beta, ...).
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=10cm]{fig/NucEmit}
\par
\end{centering}\par
\protect
\end{figure}](Timg91.gif) |
This button can save the last plotted values in either ASCII format
or ``MCNPSource Input'' format (only working for ``2D Slice''
plot)
-
-
• ASCII format: dump the last plotted data in a file.
-
-
• ``Source Input for MURE'' format: a MCNPSource C++ form file
is generated in order to be used for a MURE/MCNP simulation.
This source as the energy spectra of the selected plot, it is a collimated,
uniformly distributed on a disk of a radius of 10cm source. Particles
are emitted perpendicularly to the disk. This can be very useful for
radio-protection studies.
This button is used to load the energy binning for Spectrum from a
file . The format of this file is the same of the one used for Spectrum
class (see for example /path_to_MURE/MURE/gui/NEA_Binning_Gamma
- energies are in eV):
-
- NumberOfBins
LowerEnergy[bin=0] //lower bound of energy bin in eV
LowerEnergy[1]
...
LowerEnergy[NumberOfBins]
UpperEnergy[NumberOfBins+1] // upper bound of the last energy bin in eV
If a spectrum of a given cell or of sum of selected cells is wanted,
check the wanted cell(s) in Flux Tab.
To compute inventories, decay heat, radiotoxicity and alpha, beta,
gamma and neutron spectra of a sample over the time one can use the
option ``-onlytox'' of MureGui.
First define the sample Material :
-
- Material *MySample=new Material();
MySample->SetDensity(Density);
MySample->AddNucleus(Z,A,I,Atomes);
...
and then dump it:
-
- MySample->DumpMaterial(``SampleName'',Mass,Volume); //Mass [kg], Volume [m3]
Finally open it with MureGui :
Write in you terminal :
-
- MureGui -onlytox SampleName
The aim of these classes is to characterize any irradiated sample
in order to create elaborate sources for radioprotection studies.
Spectrum class is the base class and have not to be used directly
bu via its daugthers (GammaSpectrum, NeutronSpectrum,
...)
It's a base class to define energy spectra for
γ, β, α
and neutrons. This class defines Spectrum objects, i.e. one
array store intensities an other store energies. The size of these
array are NumberOfBins+1. To declare a Spectrum proceed
as follow :
-
- Spectrum* MySpectrum=new Spectrum(EnergyMin,EnergyMax,NumberOfBins); //Energy unit: eV
Creates a energy spectrum with a constant linear binning from EnergyMin
to EnergyMax (see Spectrum
for more options).
For non constant binning, one can use:
-
- Spectrum* MySpectrum=new Spectrum(EnergyLowVector);
where EnergyLowVector is the vector of the lower bounds of
each energy bin (NumberOfBins elements) except the last element
(the (NumberOfBins+1) of the vector which is the upper bound
energy of the last bin. Other methods allow us to build spectrum binnings
from arrays or from a file.
To build a spectrum for a particular radiation one uses the GammaSpectrum,
BetaSpectrum, AlphaSpectrum or NeutronSpectrum
classes :
-
- XSpectrum* MySpectrum=new XSpectrum(EnergyLowVector); //where X can be Alpha, Beta, Neutron or Gamma.
MySpectrum->Fill(MyMaterial,Volume);
This last method compute the alpha, beta, gamma or neutron spectrum
of MyMaterial of volume Volume.
A spectrum can be added to an other with Spectrum::AddSpectrum()
but only if the two spectra have the same energy binning:
-
- MySpectrum->AddSpectrum(SpectrumToAdd);
If you add a XSpectrum with a YSpectrum, the particle
type, that can be used for an MCNP source, is defined by the one of
the object calling the method (MyGammaSpectrum->AddSpectrum(MyNeutronSpectrum)
will have for particle type γ).
A Spectrum can be dump in a file with (if WithEnergies
is true, the energy bounds of each bin is given, else (default), the
middle energy of the bin is given) :
-
- MySpectrum->Dump(filename,WithEnergies);
All the following classes inherit from the Spectrum class:
AlphaSpectrum, BetaSpectrum, GammaSpectrum and
NeutronSpectrum.
GammaSpectrum class
In the method GammaSpectrum::ReadENSDF(Z, A, I, Atoms, DecayMode)
where Atoms is the number of atoms of the ZAI and DecayMode
is the decay mode leading to the emission of a gamma ray (it is any
combination of ``A'' (α decay), ``B'' (β- decay),
``E'' (electronic capture) and ``I'' (Isomeric Transition).
GammaSpectrum::ReadENSDF() searches in ENSDF files
the gamma transition of theZAX daughter(s) from these values
: decay constant of ZAX (λ ), Branching Ratio of
the decay (BR), Relative Intensity (RI), and the Normalization Factor
(NR). It calculates the activity A for one transition of Energy
E and fills the Spectrum:
A = λ×NZAX×RI×NR×BR/100 bq
bq![$\displaystyle \left.\vphantom{bq}\right]$](img93.gif)
where
RI×NR is the number of photon per 100 decays of the
parent for this decay branch.
RI×NR×BR is the number
of photon per 100 decays of the parent. In order to compute the gamma
spectrum of a sample, have a look in MURE/example/SpectrumExample.cxx.
Here, the method AlphaSpectrum::ReadENSDF(Z, A, I, Atoms) is
almost identical to the GammaSpectrum::ReadENSDF() one, but
it looks for alpha ray energies and intensities instead of gammas.
The method BetaSpectrum::ReadENSDF(Z, A, I, Atoms) finds in
ENSDF files decay constant, branching ratio, normalization
factor, intensity, and also the the endpoint energy (or data needed
to calculate it if it's not present, i.e. energy of the decaying level,
Q-value (ground state to ground state) of the decay and energy
of the level of the daughter)
EndPointEnergy = Qvalue + EnergyOfTheDecayingLevel - EnergyOfTheLevelOfTheDaughter
As soon as EndPointEnergy is known, the distribution f (E)
is calculated using a simplified Fermi theory where all the transition
are allowed, then for each bin, the Intensity is multiplied
by this normalized distribution.
A(E) = Atoms×λ×RI×NR×BR×f (E)
where
f (E) = Norm×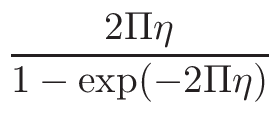 ×W×
×W×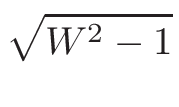 ×
× EndpointEnergy - E
EndpointEnergy - E
with
η = 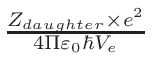 ,
Ve = c×
,
Ve = c×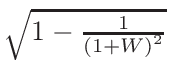 and
W = 1 +
and
W = 1 + 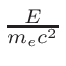 .
.
This class contains methods which are required to calculate neutron
energy spectra. Neutrons taken into account are neutrons from spontanerous
fission (NeutronSpectrum::ReadSFData method), neutrons from
 α, n
α, n reactions (NeutronSpectrum::AddAlphaNSpectra
method), and neutrons from
β-N (NeutronSpectrum::ReadENSDF
method).
reactions (NeutronSpectrum::AddAlphaNSpectra
method), and neutrons from
β-N (NeutronSpectrum::ReadENSDF
method).
The neutron spectra from spontaneous fission is computed using a normalized
Watt distribution W(E)
W(E) = Norm.exp -
- 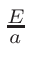
 .sinh
.sinh
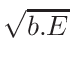
 where
a and b are coefficient depending on the nucleus.
where
a and b are coefficient depending on the nucleus.
Finally the neutron activity of the nucleus ZAX
by spontaneous fission at energy E is :
A(E) = λ×NZAX× ν
ν ×BR×W(E)
×BR×W(E)
where BR is the branching ratio of the spontaneous fission and
 ν
ν the average neutron per fission.
The parameters
the average neutron per fission.
The parameters
 ν
ν , BR, a and b
are available in literature and those used in MURE are located in
/PathToMure/MURE/data/SFNeutronSpectraData.dat [21].
, BR, a and b
are available in literature and those used in MURE are located in
/PathToMure/MURE/data/SFNeutronSpectraData.dat [21].
Neutrons can be produced by
(α, n) reactions on light nuclei
during slowing down of alpha particle in the sample. Here the reactions
taken into account are only
17O α, n
α, n Ne
and
18O
Ne
and
18O α, n
α, n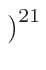 Ne. To compute neutron spectra
from these reactions, one needs alpha spectra, stopping power in the
media, cross sections leading to different level of ANe and
oxygen density (for each isotopes). Default values are natural oxygen
density in UOx fuel (
ρ = 10.4g.cm-3).
Ne. To compute neutron spectra
from these reactions, one needs alpha spectra, stopping power in the
media, cross sections leading to different level of ANe and
oxygen density (for each isotopes). Default values are natural oxygen
density in UOx fuel (
ρ = 10.4g.cm-3).
The stopping power was calculated for a UO2 media using SRIM[20],
(α, n) cross section are from JENDL(JENDL (α,n)
Reaction Data File 2005 (JENDL/AN-2005)). The probability pi
of an alpha of energy
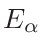 having a
(α, n)
reactions on target i while alpha slowing down on dx
is
pi = Niσidx, where
σi is the
(α, n)
cross section on target i. The probability pi can be
expressed as a function of the variation of energy of the alpha particle
on dx :
pi = Nσ
having a
(α, n)
reactions on target i while alpha slowing down on dx
is
pi = Niσidx, where
σi is the
(α, n)
cross section on target i. The probability pi can be
expressed as a function of the variation of energy of the alpha particle
on dx :
pi = Nσ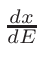 dE. By integrating the energy
of the alpha particle from it's initial energy to 0:
dE. By integrating the energy
of the alpha particle from it's initial energy to 0:
Assuming that neutrons are emitted isotropically in the center of
mass, neutrons are uniformly distributed in energy in the laboratory
system between a maximum energy and a minimum energy defined by the
conservation of momentum and energy (see for example [18]
for more information).
-
-
• This delayed neutron production has been implemented only for
(β-n)
decays ;
(β-2n) decays are not yet taken into account.
-
-
• The neutron production is taken into account only when both %
(β-n)
decays and neutron energy En is given in ENSDF files.
In july 2012, only 6 identified nuclei have this two information:
85As, 87Br, 88Br, 95Rb, 135Sb and 137I.
A computed Spectrum can be used to define a MCNP source
(see also section 4.2.2, and examples
SpectrumExample.cxx, and TubeSource2.cxx in MURE/example).
-
-
• First define the sample Material than can emits source particles (
γ, n, β).
-
-
• Then define the Spectrum (GammaSpectrum, NeutronSpectrum
or BetaSpectrum) with one of the constructors
-
-
• Finally proceed as follow (for a punctual and isotropic source) :
-
- MCNPSource *MySource=new MCNPSource(NumberOfParticle);
MySpectrum->Fill(MyMaterial,Volume);
MySource->UseThisEnergyDistribution(MySpectrum,DistributionNumber);
gMURE->SetSource(MySource);
where Volume is the Volume of your sample and DistributionNumber
is the MCNP source distribution number (default 800).
Some classes and methods are added in MURE to simplify the
building of input files or to allow more complex simulations like
the coupling of neutronics with thermal-hydraulics:
-
-
• Geometry builders : ReactorChannel, ReactorMesh
-
-
• Thermal-hydraulics flow simulation class : COBRA_buidfile,
COBRA_constructor, COBRA_reader.
-
-
• BATH (Basic Approach of Thermal Hydraulics) : ThermalCoupling,
ThermalDataReader.
Coupling (like the examples given in MURE/examples)
is relevant only if temperature dependent cross-sections for MCNP
have been provided for each isotope.
Simulations of nuclear power plants can need a discretization of the
core in 3 dimensions. The accuracy required by users defines the thinness
of the core's mesh. If the latter is important, the building of the
MURE input file could be very complex. This is the reason
why new tools were added to MURE : ReactorChannel
and ReactorMesh. They don't add new physics sections into MURE
but only use MURE classes to easily create specific input
files. ReactorChannel is a MURE compound and creates
multi-cellular objects: it can be used to simulate complex cores with
different geometries of pins depending on their position in the core.
-
-
• ReactorMesh is a MURE class with a double use: it
manages filled assembly geometry, and it is used for a coupled analysis
with thermal-hydraulics. It helps users to create geometry for basic
squared lattice of a reactor assembly. Channels are, together with
cylindrical fuel rod and cladding, split up into α sections
(levels) in the Z direction, and β zones in (X,Y)
direction. It manages guide tubes containing coolant or control rods
and special tubes with an annular or more complex pin cell geometry.
All data must be given in SI (distances in meters, power in watts,
...).
-
-
• COBRA class has been created for the coupling analysis with
a qualified thermal-hydraulics sub-channel code : COBRA-EN[10,11]
(Coolant Boiling in Rod Arrays). The coupling is completely transparent
for users: the input file do not differ from a usual neutronics simulation
input file.
-
-
• BATH solves the heat equation in case of a permanent regime and a
cylindrical fuel and cladding shapes. The following estimates should
be taken into account:
-
-
• heat conduction is calculated in homogeneous isotropic media (temperature
only depends on radius)
-
-
• simulations are done on average elementary channel(s) (no cross-flow).
Several ``average'' channels can be simulated but thermal-hydraulics
interactions between them cannot be calculated.
-
-
• The code only simulates a liquid phase (no boiling).
A nuclear reactor is mainly controlled by two disciplines: neutronics
and thermal-hydraulics. In fact, reactor core temperatures depend
on the heat sources, and thus on the distribution of power which evolves
in the course of time (calculated by neutronics codes). Yet, these
codes require cross sections which depend on the temperatures, and
thus on the nature of flow that is solved by thermal-hydraulics codes.
The input file for a coupled analysis is the same than a pure neutronics
MURE calculation. Of course, some thermal-hydraulic characteristics
must be added (like coolant temperature entrance, pressure,...) but
a non thermal-hydraulic physicist can quickly perform a simulation
with a thermal-hydraulics coupling. The generation of the COBRA
input file happens automatically and without any user intervention
as well as the coupling procedure between
MURE and COBRA.
The neutronics code calculates the power distribution in the fuel
pins, which is transferred to the thermal-hydraulics code. Then, this
latter determines new properties in each pin and sub-channel (temperatures,
densities,...). Finally, these data are used as new inputs for the
next neutronics calculation. Iterations can be repeated until a converged
state is obtained or during a step time for an transient analysis.
Meshing grids are different between neutronics and thermal-hydraulics
(c.f. figure 8.1).
Figure 8.1:
Meshing grids.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=8cm]{fig/grids}
\par
\end{centering}\par
\protect
\end{figure}](Timg121.gif) |
In fact two different physics disciplines are dealt with, but their
solving methods have nothing in common. This is the reason why two
different meshes are defined. Consequently classes manage the correspondence
and the symmetrization of these meshes. Updates are done using mean
values by zones (c.f. figure 8.2).
Figure 8.2:
Radial zones and axial levels.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=14cm]{fig/zones}
\par
\end{centering}\par
\protect
\end{figure}](Timg122.gif) |
These zones are chosen by the user and are dependent on the precision
required. In each radial zone and axial level, neutron flux, reaction
rates, properties of materials or coolant and fuel burn-up are treated
separately.
Any increase in the discretization must be carefully
considered because it may use more computing resources for a marginal
accuracy gain, or even, in certain circumstances, cause a loss of
precision.
The use of this class is needed for the neutronics/thermal-hydraulics/thermics
coupling. Nevertheless it can also be used only for neutronics simulation
as a simplified way of building geometries.
Construction of materials and sizes of frames is the same as for a
MURE calculation. Differences are on the meshing of assemblies.
The first step is to build the internal structure of the assembly:
-
- Shape_ptr AssemblyShape1(new Brick(AssemblyLenght/2.0, AssemblyLenght/2.0, ReactorHeight/2.0));
Then the user defins a ReactorMesh object that manages
the mesh, the duplication of materials and structures:
-
- ReactorMesh* Assembly1 = new ReactorMesh(7,20); // 7 radials zones, 20 axial levels
It is necessary to specify some frame details:
-
- Assembly1->SetExternalShape(AssemblyShape1); // physical limits
// dimensional definition of the constituent elements:
Assembly1->SetDimensions(FuelPelletRadius, CladdingTubeThickness, CellPitch);
//
// Automatic differentiation of zones for structurally identical elements
// (c.f. fig 8.2)
Assembly1->AddCircleZoneRadius(3*CellPitch);
Assembly1->AddCircleZoneRadius(6*CellPitch);
Case of a same isotopic vector for materials :
-
- Assembly1->AddMaterials(FuelMat, CladdingMat, CoolantMat);
Or else, specify for each zone :
-
- Assembly1->AddMaterials(FuelMat0, CladdingMat0, CoolantMat0,0);
Assembly1->AddMaterials(FuelMat1, CladdingMat1, CoolantMat1,1);
Assembly1->AddMaterials(FuelMat2, CladdingMat2, CoolantMat2,2);
It can be possible to make more complex geometries, like using exotic
pins with for example two fuel zones in a pin :
-
- // make explicit the zone
Assembly1->SetSpecialDimensions(FuelPelletRadius, CladdingThickness, CellPitch, FirstInnerRadius, SpecialPinZone);
Assembly1->SetSpecialMaterials(FuelMat, CladdingMat, CoolantMat, SPFuelMat, SpecialPinZone);
...
Tube guides can also be introduced :
-
- Assembly1->SetGTDimensions(GuideTubeInnerRadius,GuideTubeThickness);
Assembly1->SetGTMaterials(GuideTubeInsideMat,GuideTubeCladdingMat);
The coolant around this guide tubes is the same as the ones for neighbours
cells (same composition, bore concentration, temperature, density,
...).
The placing of SpecialPins and GuideTubes is done using
their relative position into a Cartesian reference mark centered on
the first cell built by MCNP (center cell of assembly identified
as (0,0)).
-
- Assembly1->AddSpecialPin(1,4,SpecialPinZone);
Assembly1->AddGuideTube(-3,0);
Construction of the MCNP geometry is automatically done when
users call the method (c.f. figure 8.3) :
-
- Assembly1->CreateGeometry();
Figure 8.3:
Complex Mesh.
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=14cm]{fig/NewMesh2}
\par
\end{centering}\par
\protect
\end{figure}](Timg123.gif) |
Call of MURE::BuildMCNPFile() or MURE::RunMCNP() methods
are performed as during a basic MURE input file, no modifications
or adjustments are necessary.
See the documented example in MURE/examples.
-
-
• Translate assembly into another position in the core
-
- Assembly1->Translate(dx,dy,dz);
-
-
• Create plenum for an assembly
-
- Assembly1>>AssemblyPlenum; // must be done after the call of CreateGeometry()
-
-
• Set a maximum volumic source contained inside the assembly with a
Watt spectrum
-
- Assembly1->SetSource(NumberOfParticles, ActivesCycles, InactivesCycles);
See the documented example MURE/example/Evolution/RMAssembly.cxx
(c.f. figure 8.4).
Figure 8.4:
Example of an assembly created with ReactorMesh
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=14cm]{fig/RMAssembly}
\par
\end{centering}\par
\protect
\end{figure}](Timg124.gif) |
Most of the input file for a coupled calculation does not change compaer
to a pure neutronics calculation: instead of creating a ReactorMesh
object, it is necessary to build a COBRA one (COBRA
class inheritsfrom ReactorMesh class). An additional
method must be called to allow the building and launching of thermal-hydraulics
calculations.
Thus, instead of:
-
- ReactorMesh* Assembly1 = new ReactorMesh(7,20);
one should use:
-
- COBRA* Assembly1 = new COBRA(7,20);
and add:
-
- FuelMat->SetEvolution(); // flag needed for power deposits calculation
// set the flag on each fissionable fuel material
gMURE->BuildTallies(); // Tallies are managed by MURE
gMURE->BuildCOBRAFiles(); // call of this method after the RunMCNP()
// it manages creation of input(s) data file(s) to COBRA with the power
// distribution calculated by MCNP and update densities and temperatures
A file called MeshZoneData.txt is created: the number of fuel
pins, guide tubes, special pins for each zone are quoted ; an equivalent
of the mesh MCNP - Zones is also written.
This class manages the Oak Ridge National Laboratory code COBRA-EN
(COolant Boiling in Rod Arrays). It is a sub-channel code that allows
steady-state and transient analysis of the coolant in rod arrays.
The simulation of flow is based on a three or four partial differential
equations: conservation of mass, energy and momentum vector for the
water liquid/vapor mixture (optionally a fourth equation can be added
which tracks the vapor mass separately). The heat transfer model is
featured by a full boiling curve, comprising the basic heat transfer
regimes: single phase forced convection, sub-cooled nucleate boiling,
saturated nucleate boiling, transition and film boiling. Heat conduction
in the fuel and the cladding are calculated using the balance equation.
Some modifications on the source code have been done to optimize calculations
on Intel Fortran Compilers (ifort) and to enlarge arrays (parameters
IDSIZE in source files).
Some precisions about fluid mechanics must be given. Otherwise, default
values are taken into account.
Inlet temperature (K) :
-
- Channel1->SetInletTemperature(560);
Average inlet mass flux
(kg/s/m2) :
-
- Channel1->SetInletMassFlux(2923.72);
Inlet boron concentration (ppm) :
-
- Channel1->SetInletBoronConcentration(1000);
System exit pressure (MPa) :
-
- Channel1->SetExitPressure(15.8);
See the documented example MURE/example/Thermal/C4Assemblies.cxx
(c.f. figure 8.5) and some results
:
-
-
• Power distribution: figure 8.6a
-
-
• Exit coolant temperature profile: figure 8.6b.
Figure 8.5:
Geometry visualization
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=10cm]{fig/coupe_react}
\par
\end{centering}\par
\protect
\end{figure}](Timg125.gif) |
Figure 8.6:
Complex COBRA coupled simulation : 20 axial levels and 4*7 radial
regions
![\begin{figure}\endgraf
\centering {} \subfloat[3D Power distribution (W)]{\begi...
...udegraphics[width=8cm]{fig/Tout}
\par
\end{centering}\par
}\protect
\end{figure}](Timg126.gif) |
This class manages temperature calculation for a coupled simulation
neutronics/thermal-hydraulics with a 2D RZ precision.
It is not as accurate as COBRA and must be explicitly coupled by the
user but its advantages are :
-
-
• the capability to be coupled with geometry that has already bee built
-
-
• it is an explicit way of coupling, despite the fact it takes longer,
users can completely control what is being simulated (it is not a
``black box'')
-
-
• capability to simulate a lot of coolant, cladding or fuels types:
users just need to add them (thermal data and equations).
The code already includes data and equations necessary for simulations.
It uses:
-
-
• as fuel: uranium oxide and plutonium/uranium mixed oxide and thorium
oxide (full or annular pellet)
-
-
• as cladding: zircaloy 4 or 2 and stainless steel 316 SS
-
-
• as coolant: light water, heavy water and sodium.
-
-
• heat and mass transfer:
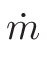 CpΔT = qpA
CpΔT = qpA
-
-
• steady-state forced convection in case of turbulent flows:
Tp - 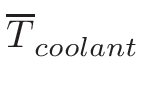 =
= 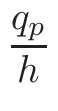
-
-
• steady-state conduction inside the cladding and the fuel: Fourier
law
-
-
• radiation exchange between cladding and fuel surfaces is implemented
but not used (due to a leak of precision on gas composition and evolution
of the gas space dimension during burn-up): Stefan law
-
-
• indication of pressure losses (due to acceleration, gravity and friction
- loss due to peculiarity like grids are not calculated because it
is considerd as empirical data): acceleration is zero because the
velocity is assumed constant, only gravity and friction (Darcy frictions
model) are calculated
-
-
• thermal conductivity of zircaloy and steel, data on water, sodium,
UOX and MOX are from literature.
-
-
• Nusselt dimensionless number calculation:
-
-
• water: Dittus-Boelter equation
Nu = 0.023 Re0.8Pr0.4
-
-
• sodium: Notter & Sleicher
Nu = 6.3 + 0.0167 Re0.85Pr0.93
If thermal conductivity of new cladding is needed, one has to modify
the source of ThermalCoupling class, adding flags and switching
cases in ThermalCoupling::CladConduction().
To add a new coolant, equations of dimensionless number calculation
are perhaps necessary and data tables must be added in thermal_data
directory. As it is done for water and sodium, files
containing thermal data must be created : see Water.xls in
thermal_data directory.
Adding a new fuel is easier: only 2 tables of data are necessary (density
and thermal conductivity : see thermal_data directory).
Contact Nicolas Capellan (capellan at ipno.in2p3.fr) for further
explanation.
Users should create the geometry themselves. Flags will be added to
indicate positions of frames and cells to the thermal-hydraulics code
:
-
-
• on materials: flag SetTemperatureEvolution() and only on fuel
material SetEvolution()
-
-
• on cells: flag(s) SetTHLevelPosition() (the first one at the
bottom and then increasing height) and SetTHZonePosition()
if more than one average channel is needed.
BATH is created and launched after the MCNP run.
See the documented example MURE/examples/Thermal/BATHExample.cxx.
Outputs are created in the directory called Zi_Run_j (i
is the ``region'' and j the iteration number of coupled field).
For each level, thermal results are built together with the temperature
function of distance from the center (temperature gradient inside
fuel, cladding and coolant, c.f. figure 8.7).
Figure 8.7:
BATH output example
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=9cm]{fig/ASTH}
\par
\end{centering}\par
\protect
\par
\end{figure}](Timg130.gif) |
Basic of C++ to understand MURE
This appendix is not a C++ tutorial ; its aim is to define roughly
commonly used words inside MURE user guide and to allow users unfamiliar
with C/C++ to understand examples and uses of MURE. Each main program
in C++ is defined as
-
- int main() //or int main(int argc, char **argv) to use argument passed to the program
{
...
}
In general, special functions, variables, ... are needed. Then, the
definition of these functions known as the header files should be
included:
-
- #include <iostream> //standard functions for input/output on the screen (cout, cin, ...)
#include <cmath> //standard mathematical function (cos, sin, ...)
using name space std;
#include ``my_header_file.hex'' //a definition made by a user
int main()
{
...
}
C++ is said Object Oriented. This means that the notion of
variables is extended to a more complete and self consistent form:
the object. The variable types are now called classes:
for example, the type float of C (real in fortran)
is now a class. For this class the difference between type
and class is simply semantic. But you can create your own type
(your own class) that regroups many other objects (or variables
in C/fortran language) of different classes (different types). For
example a class Point can have 2 coordinates of the class double:
-
- class Point
{
public:
double X;
double Y;
};
The ``public:'' keyword means that one can use the objects
of this class from the outside of the class. The 2 objects X
and Y are called members or attributes of
the class Point. To declare an object P of the class
Point to be a point of coordinates (0,4), one has to
-
- Point P;
P.X=0;
P.Y=4;
Moreover, a class contains methods, that is to say, specific
functions that can act only on objects of this class:
-
- class Point
{
public:
void Translate(double dx, double dy) {X+=dx;Y+=dy;}
double X;
double Y;
};
P can be translated of
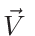 (1, 1):
(1, 1):
-
- P.Translate(1,1);
Special methods of classes are named constructors: these
methods have no type and name of the class ; they are
used to allocate memory and eventually initialize an object:
-
- class Point
{
public:
Point(double x, double y){X=x; Y=y;}
void Translate(double dx, double dy){X+=dx;Y+=dy;}
double X;
double Y;
};
Then P can be declared as
-
- Point P(0,4);
Methods (as well as functions) can be overloaded: 2 methods
may have the same name but different arguments:
-
- class Point
{
public:
Point(double x, double y){X=x; Y=y;}
Point(){X=0; Y=0;}
void Translate(double dx, double dy){X+=dx;Y+=dy;}
void Translate(double dV[2]){X+=dV[0];Y+=dV[1];}
double X;
double Y;
};
here the second constructor has no argument ; it is called
the ``default constructor'' ; in this case it defines the
origin point ; the second Point::Translate() method needs an
array of dimension 2 as argument:
-
- Point P1; //call the default constructor
Point P2(0,4); // call the ``normal'' constructor P2 is (0,4)
double dv[2]={1,1}; //an array of 2 doubles
P1.X=2; //set X of P1
P1.Y=2; //set Y of P1;
Point P3=P1; //P3 is (2,2)
P1.Translate(dv); //Translate P1 from (2,2)->(3,3) but P3 is still at (2,2)
P2.Translate(1,1);//Translate P2 from (0,4)->(1,5)
It is usually safe to ``protect'' the objects of a class
from modifying them from the outside of the class without using a
class method. One may succeed by using the ``private:''
keyword. But then one must define new methods to modify them.
-
- class Point
{
public:
Point(double x, double y){X=x; Y=y;}
Point(){X=0; Y=0;}
void Translate(double dx, double dy){X+=dx;Y+=dy;}
void Translate(double dV[2]){X+=dV[0];Y+=dV[1];}
void SetX(double x){X=x;}
void SetY(double y){Y=y;}
double GetX(){return X;}
double GetY(){return Y;}
private:
double X;
double Y;
};
Then, one should not write
-
- P.X=1;
cout<<''Coordinate of P(''<<P.X<<'',''<<P.Y<<'')''<<endl;
but instead, use
-
- P.SetX(1);
cout<<''Coordinate of P(''<<P.GetX()<<'',''<<P.GetY()<<'')''<<endl;
Of course, this is not very useful for this simple example ; but for
larger codes, it avoids bugs.
In the previous class Point, one has defined explicitely all
methods inside the class. But when dealing with larger classes, libraries,
please consider separating the class definition (.hxx files
called headers) from the class implementation (.cxx
files). Then, one may build libraries with implementation files whereas
the header files could be included in any file using the library.
For example one may rewrite the Point class header in the Point.hxx
file
-
- class Point
{
public:
Point(double x, double y);
Point();
void Translate(double dx, double dy);
void Translate(double dV[2]);
void SetX(double x){X=x;} // here thes methods are very short,
void SetY(double y){Y=y;} // one can let then with inline definition.
double GetX(){return X;}
double GetY(){return Y;}
private:
double X;
double Y;
};
Not the ``;'' after the first 4 methods: it means that
they will be defined somewhere else. The Point.cxx implementation
file:
-
- #include ``Point.hxx''
Point::Point(double x, double y)
{
X=x;
Y=y;
}
Point::Point()
{
X=0;
Y=0;
}
void Point::Translate(double dx, double dy)
{
X+=dx;
Y+=dy;
}
void Point::Translate(double dV[2])
{
X+=dV[0];
Y+=dV[1];
}
Note the ``Point::'' ; it means that the following method
belongs to the class point (``::'' is the scope resolution
operator).
In MURE, lots of parameters have default values. In general default
values are assigned in methods (or function) definitions (header files)
with the following syntax:
-
- void TheMethod(double x=3);
This means that if one calls TheMethod(5), the value of the
argument x=5, whereas a call to TheMethod() will
take x=3 for this ``default'' argument. If one
writes
-
- void AnOtherMethod(double x, double y=2);
The first argument must be given and the second one (y), if
it is not given, takes the value y=2. All default
arguments must be defined after the explicit argumentA.1. If one writes
-
- void ThirdMethod(double x=1, double y=2, double z=1);
then a call to
-
- ThirdMethod(); // means that x=1, y=2, z=1
ThirdMethod(3); // means that x=3, y=2, z=1
ThirdMethod(3,10); // means that x=3, y=10, z=1
ThirdMethod(3,10,100); // means that x=3, y=10, z=100
We have defined objects of classes. One can define pointers
on objects:
-
- Point *P1=new Point; //call the default constructor
Point *P2=new Point(3,4); //call the normal constructor
P1->SetX(1); //because P1 is a pointer on a Point, one use ``->'' instead of the ``.''
P2->Translate(1,1);
Point *P3;
P3=P1; //P3 and P1 are pointing on the same Point (1,0)
P3->Translate(1,1); // P3 and P1 point on (1,1).
Point *P;
P=new Point[3]; //P is an array of 3 Points (it points on the first)
for(int i=0; i<3; i++)
{
P[i].SetX(2*i+1); //P[i] is a Point (whereas P is a pointer)
P[i].SetY(i+1); //thus one uses a ``.'' and not the ``->''
}
P[0].Translate(1,1); //Translate P[0] from (1,1)->(2,2)
delete P1;
delete P2;
delete [] P;
The 2 first lines allocate 2 Points (the ``new'' keyword).
One use the ``->'' instead of the ``.'' to use
a method (or a public attribute) because P1 and P2 are
pointers. In the declaration of P3, no Point is allocated (no
``new'') ; the ``P3=P1'' line means that P3
points on the same Point than P1 ; thus translating P3
will translate P1 (and vice verse). By writing ``P=new
Point[3]'', one allocates an array of 3 Points by calling the
default constructor of Point (to declare arrays, a default
constructor must exist). Each P[i] is a real Point object
(not a pointer). When one use pointers, the memory is not freed by
itself: one has to do it manually though a ``delete''.
Here one can delete P1 or P3 but not both ; in the example,
P3 continues to point on the address of the P1 Point,
but because the memory has been freed, this address does not correspond
to anything. To delete arrays, one has to use the ``[]''
after the ``delete'' keyword.
One very powerful tools of classes is the inheritance
mechanisms. One says that a class inherits from a mother class:
all members (methods and attributes) of the mother class are known
from the Daughter class. This one may have new methods and/or attributes.
Following our previous example, one can define a Point3D as:
-
- #include ``Point.hxx''
class Point3D : public Point //here one says that Point3D is the daughter of Point
{
public:
Point3D():Point(){Z=0;}
Point3D(double x, double y, double z):Point(x,y){Z=z;}
void Translate(double dx, double dy, double dz){X+=dx;Y+=dy; Z+=dz;} //possible if the ``private:'' of Point
void SetZ(double z){Z=z;} //is replaced by ``protected:''
double GetZ(){return Z;}
private:
double Z;
};
and one has to replace the keyword ``private:'' of the
class Point by the keyword ``protected:'' in order
to allow the Daughter of Point (Point3D) to modify its
attributes. But from the outside of Point and Point3D, it is impossible
to modify these attributes. The 2 constructors of Point3D start
to call respectively the default and the normal constructor of the
mother class (:Point() and :Point(x,y)).
-
- Point3D P1(1,2,3); // P1 is at (1,2,3)
Point3D P2; //P2 is at (0,0,0)
P2.SetX(1);
P2.SetY(1);
P2.SetZ(1); //P2 is now at (1,1,1)
P1.Translate(1,1,1); //P2 is now at (2,2,2);
Node tree simplification
In this appendix, more details are provided on the principle of the
Node simplification to obtain more optimized MCNP input files. For
example, in figure B.1 the Plane number 2 belongs
to 2 Nodes and must not be destroyed after the destruction of the
included node.
Figure B.1:
A tree corresponding to a geometrical object before its simplification.
The representation tells whether a node is a union or intersection,
then the node address is given, the address of the not of the node
(complementary node) is also given if it exists. Nodes in red are
usually not removable because of included, bounding or inside shapes
(see Node class). For each leaf of the tree, the type of Shape (Plane,
Sphere, ...) is given as well as its address and its surface number
with a sign (like in surface in MCNP cell).
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=14cm]{fig/tree_disjoint}
\par
\end{centering}\par
\protect
\end{figure}](Timg132.gif) |
Figure B.2:
The tree of figure B.1 after simplification. Since
one node was included in the other, it has been removed.
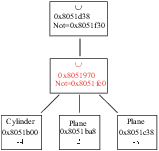 |
Figure B.3:
An other example of tree before simplification.
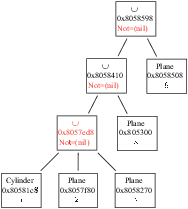 |
Figure B.4:
The tree of figure B.3 after simplification.
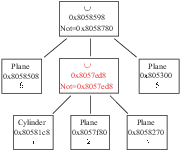 |
WARNING: UP TO NOW SURFACE CALCULATIONs HAVE NOT YET
BEEN IMPLEMENTED.
When using Tallies, cell volumes and/or surfaces are needed. In this
package, cell volumes are calculated if possible ; when the program
is not able to calculate cell volumes for a tally, we use the method
MURE::BuildMCNPFile() to extract the volume calculated by MCNP
itself (see note C.1).
However, sometimes MCNP is not able to calculate the volume/surface
of a Cell. Thus, a stochastic volume calculation is made (again
using MCNP). The principle of this calculation is to take a neutron
source geometry of a spherical shell directed inwards containing the
necessary cells filled with voids. The required volumes are calculated
stochastically by MCNP from the number of particle tracks which have
intersected them.
The precision on volumes will depend on the source neutron number
(that can be modified via MURE::SetVolumeNPS()) as well as
the relative size of the cell/source neutron sphere. In the usual
procedure, a source sphere containing the whole geometry is searched ;
However, the search can sometimes fail, in which case the user is
required to give the source sphere characteristics manually with the
command:
-
- Shape::SetVirtualSphereRadius()
and
-
- Shape::SetVirtualSphereCenter()
It should be noted that it is not necessary for the whole geometry
to be included in the ``virtual'' sphere ; only cells with unknown
volumes must be inside this sphere. A volume warning message is given
if the relative precision of the worst volume variance is below 0.5% ;
this precision may be change with MURE::SetVolumeWarning().
Important Note
Stochastic volume calculations are used if a tally bin has a volume
equal to -1. The tally bin volume is taken from the cell used in this
bin. Cell volumes are determined from Shape volumes. Sometimes, we
are unable to determine relatively simple Shape volumes because the
Inclus/Disjoint method can't return a result (e.g., a shape
may be included in another one, but Shape::Inclus() answers
0 (i.e., not included or unknown)). For these cases it is necessary
to avoid stochastic volume calculations, whereas if MCNP is able to
calculate the volume of such cells, we can use the method MURE::GetMCNPVolume().
The principle of this method is to ``run'' MCNP in ``information
mode'', then search the print table 60 containing the cell volumes
information. For a cell without a volume (i.e. -1), if the volume
has been calculated and if the cell has no universe numberC.1, then the cell volume is set to what MCNP has calculated.
To summarize, the MURE::BuildMCNPFile() method calls first
MURE::GetMCNPVolume() ; then, if necessary, the MURE::FindMissingVolume()
method (stochastic volume calculation technique) is called and afterward
the input MCNP file is written.
NOTE: The tally bin volumes should always be provided ;
thus, if a group bin or a lattice bin is used, the calculated volume
related to that bin...but not to each individual cell composing the
bin. Therefore, the individual cell volume remains unknown.
Steady-state power: Tally Normalization
MCNP provides raw tallies normalized by source neutron. For reactor
applications, in order to simulate a constant reactor powerD.1, one must normalize all tallies by the equivalent number of neutrons
per second for a user-given power value. This normalization factor
will change as the isotopic composition of the material evolves with
time and therefore needs to be calculated at the lowest level of time
discretization, i.e., at every RK step, and, a fortiori, also
every time neutron transport is performed.
-
-
• Constant power P is defined by the user once and for all throughout
the evolution using the gMURE->SetPower()
function . This value is translated into the number of fissions per
second.
-
-
• At every MCNP step, flux φ and average reactions cross-sections
σiare read from MCNP output for every nucleus in
every cell. Isotopic proportions are read from the initial user-defined
composition and for all subsequent steps these values are solved according
to their Bateman equations.
-
-
• At every RK step average cross-sections
σi, read in the
prior MCNP step, have (so far) been kept constant. New values for
the isotopic proportions Ni+1 are solved for using former values
of other parameters. P is constant by definition : a new value of
the tally normalization factor is therefore calculated in order to
keep P constant.
The energy released per fission is around 200 MeV, but the exact value
varies by +/- 5% and varies primarily with the mass of the fissile
isotope.
By default MURE assumes that the energy released from fission for
each fissionable isotope is different. For several common fissile
isotopes, the fission energy values are taken from: W.H. Walerk, ``Mass
balance estimate of energy per fission in reactors AECL-3109, 1968''.
For all other fissionable isotopes, fitted values are used. The linear
fit (as a function of mass) is made for the common isotopes [232Th
- 241Pu] and extrapolated to the uncommon ones.
For example (see [17]), in the case of 235U, the
energy released by fission Q is given in Table D.1.
Table D.1:
Energy Released per fission for 235U.
| Fission Product kinetic energy |
166.2±1.3 MeV |
| Prompt fission γ |
8.0±0.8 MeV |
| Delayed (after β decays) γ |
7.2±1.1 MeV |
| β decays |
7.0±0.3 MeV |
| Neutron kinetic energy |
4.8±0.1 MeV |
|
(n, γ) capture(
6 MeV ×1.42 neutrons) |
8.5 MeV |
| Energy released Q |
201.7±0.6 MeV |
In MURE, the default value is
Q235U = 201.7 MeV.
The energy of neutrinos (in this case, 9.6 MeV), is not taken into
account.
If a user wishes to use specific values, 2 methods are available.
The first one, MURE::SetAllFissionEnergies() allows to give
a common constant value to each fissionable isotopes (default=200
MeV) ; the second method, MURE::SetFissionReleasedFile() allows
user to give a file with the required value for some (or all) fissionable
isotopes. Each line of the file is
-
- Z A Qvalue
where Z and A are the proton and nucleon numbers and Qvalue is the
energy released by fission (in eV). When using this method, the Q
values are taken as explained above (using the linear fit) except
for the isotopes specified in this file.
NOTE: MURE::SetAllFissionEnergies()
and MURE::SetFissionReleasedFile()
must be called BEFORE any Material declaration
to be taken into account.
The fact that MURE takes into account different fission energy released
values, means that there will be slight differences in the way the
normalization factor is calculated, and therefore slight difference
in inventory when the fissile nucleus changes as a function of time
when compared with the old method.
The total power delivered by the total number of fissions in a given
instant (in MCNP raw units) is given by the double sum shown
hereafter :
Pmcnp = 
 Nijσijφ mcnpjξ
Nijσijφ mcnpjξ
where the subscript i refers to the nucleus considered whereas
j refers to the cell considered. The sum is to be carried out
over all cells and all nuclei belonging to each cell's material.
Pmcnpcan be thought of as the power delivered per source particle
transported in the global geometry in question : If φj is
in standard MCNP type 4 tally output units (particles per unit
surface per source particle) then
Pmcnp will be also
normalized per source particle.
-
-
• Nijis the number of nuclei i present in cell j.
-
-
•
σij is the average fission cross-section
of nucleus i in cell j.
-
-
• φj is MCNP's neutron flux track-length estimation for cell
j.
-
-
• ξ is the average energy delivered in one fission (∼200
MeV).
Therefore, the scaling factor α, by which tallies will be
normalized and which has to be taken into account in order to simulate
a constant burn-up at the desired power
Puser (if Puseris
provided in watts and ξ in eV) is written :
α≡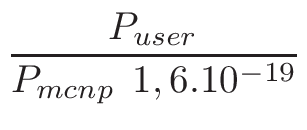 =
= 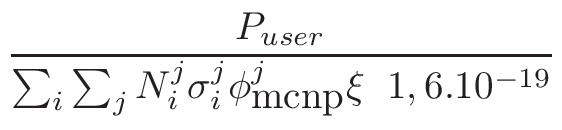
For a critical system, if one multiplies the desired power
in fissions per second times the average number ν of neutrons
emitted per fission, one obtains the amount of existing neutrons in
the geometry at a given instant. This can be thought of as the intensity
of the neutron source needed to achieve this desired power. This value,
in neutrons per second, should be equivalent to the value of α
calculated in the previous paragraph. If the system is critical (Keff = 1)
this number is constant during a time interval small enough so that
the amount of fissile material remains unchanged in a first approximation.
If the system is critical and Puser is in watts and ξ
in electron-volts, then:
α≅ν 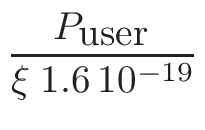
For our problem example, the first method gives a value of alpha of
roughly
8.280 10+12 whereas the second method gives a value
of
8.124 10+12 with νtaken at 2.599. The two values are
therefore comparable within less than 2 percent.
- 1
- Méplan O., Nuttin A., Laulan O., David S., Michel-Sendis
F. et al., ``MURE : MCNP Utility for Reactor Evolution - Description
of the methods, first applications and results'', Proceedings of
the ENC 2005 (CD-Rom) - ENC 2005 - European Nuclear Conference. Nuclear
Power for the XXIst Century : From basic research to high-tech industry,
France
- 2
- Michel-Sendis F., Méplan O., David S., Nuttin A.,
Bidaud A. et al., ``Plutonium incineration and uranium 233
production in thorium fueled light water reactors'', GLOBAL 2005
Proceedings (CD-Rom) - GLOBAL 2005: International Conference on Nuclear
Energy Systems for Future Generation and Global Sustainability, Japon
- 3
- X-5 Monte Carlo Team, ``MCNP --
A General Monte Carlo N-Particle Transport Code, Version 5'', Los
Alamos National Laboratory report LA-UR-03-1987 (April 2003)
- 4
- J.S. Hendricks, G.W. McKinney, H.R. Trellue, J.W.
Durkee, T.L. Roberts, H.W. Egdorf, J.P. Finch, M.L.Fensin, M.R.James,
D.B.Pelowitz, and L.S. Waters, ``MCNPX version 2.6.A'', Los
Alamos National Laboratory report LA-UR-05-8225 (2005)
- 5
- H.R. Trellue and D.I. Poston, ``User's
Manual, version 2.0 for MONTEBURNS, version 5B'', Los Alamos National
Laboratory report LA-UR-99-4999 (1999)
- 6
- ``SCALE: A Modular Code System for Performing
Standardized Computer Analyses for Licensing Evaluations'', ORNL/TM-2005/39,
Version 5.1, Vols. I-III, (2006).
- 7
- R. S. Babcock, D. E. Wessol, C. A. Wemple, and S.
C. Mason, ``The MOCUP Interface: A Coupled Monte Carlo/Depletion
System'', 1994 Topical Meeting on Advances in Reactor Physics, Knoxville,
TN, p. III-368 (April 11-14, 1994)
- 8
- J. Cetnar, W. Gudowski and J. Wallenius, ``MCB:
A continuous energy Monte Carlo Burnup simulation code'', In ``Actinide
and Fission Product Partitioning and Transmutation'', EUR 18898 EN,
OECD/NEA (1999) 523.
- 9
- R. E. MacFarlane and D. W. Muir, ``The NJOY
Nuclear Data Processing System Version 91'', Los Alamos National
Laboratory report LA-12740-M, (October 1994).
- 10
- Jason Chao, ``COBRA-3C/RERTR - A Thermal-Hydraulic
Subchannel Code with Low Pressure Capabilities'', Science Applications,
Inc. (December 25, 1980)
- 11
- D. Basile, R. Chierici, M. Beghi, E. Salina and
E. BregaCOBRA-EN, an Updated Version of the COBRA-3C/MIT Code for
Thermal-Hydraulic Transient Analysis of Light Water Reactor Fuel Assemblies
and Cores Report 1010/1 (revised 1.9.99)
- 12
- J.R. Parrington et al., ``Nuclides and
Isotopes", 15th edition, General Electric Nuclear Energy,
1996
- 13
- R.B.Firestone, "Table of Isotopes",
8th edition, V.S.Shirley editor, John Wiley & Sons, Inc, 1996
- 14
- W. Haeck, B. Verboomen, ``An optimum
Approach to Monte Carlo Burn-Up'', Nucl. Sci. Eng.,
156, pp 180-196 (2007)
- 15
- J. Miss, O. Jacquet, F. Bernard, B. Forestier, W.
Haeck, Y. Richet, ``First validation of the new continuous
energy version of the MORET5 Monte Carlo code'',
PHYSOR 2008
- 16
- E. Brun, E. Dumonteil and F. Malvagi, ``Systematic
Uncertainty Due to Statistics in Monte Carlo Burnup Codes: Application
to a Simple Benchmark with TRIPOLI - 4 - D'', Progress in Nuclear
Science and Technology, Vol. 2, pp.879- 885 (2011)
- 17
- M.F. James, Journal of Nuclear Energy,
23, 517 (1969)
- 18
- W.B. Wilson, M.Bozoian and R.T. Perry
(1988) ``Calculated α induced thick target neutron yields
and spectra,with comparison to measured data''
- 19
- Neutron and Gamma-Ray Fluence to Dose Factors,
American National Society, ANSI/ANS-6.1.1-1977
- 20
- James F. Ziegler, ``The Stopping
and Range of Ions in
Matter (SRIM)'', http:www.srim.org
- 21
- E.F. Shores, ``Data update for SOURCE-4A
computer code'', Nuc. Inst. Meth. B, 179, (2001), pp 78-82
- 22
- M. Oettingen et al., ``Comparison of MCB and
FISPACT burn-up performances using the HELIOS experiment technical
specifications'', Nuc. Eng. and Design, 242, (2012), pp 399-412



Previous: "Class_Summary"

![\begin{figure}\endgraf
\begin{centering}
\includegraphics[scale=0.8]{fig/classe}
\par
\end{centering}\par
\protect
\end{figure}](Timg2.gif)
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=10cm]{fig/put_in}
\par
\end{centering}\par
\protect
\end{figure}](Timg3.gif)
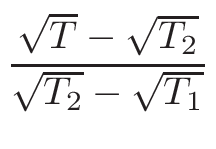
![]() ,
it is not printed. The value of
,
it is not printed. The value of
![]() is by default set to
0.1%×1mb = 10-6. This can be changed via MURE::SetMCNPNucleusThreshold().
To be noticed that perturbative tallies of all evolving nuclei are
written (in order to evaluate the cross-section...). The effect of
this procedure is thus to accelerate MCNP runs at the beginning
of the evolution where time steps between MCNP are smaller,
and add more and more nuclei as far as the evolution is going on (with
bigger time steps between MCNP runs).
is by default set to
0.1%×1mb = 10-6. This can be changed via MURE::SetMCNPNucleusThreshold().
To be noticed that perturbative tallies of all evolving nuclei are
written (in order to evaluate the cross-section...). The effect of
this procedure is thus to accelerate MCNP runs at the beginning
of the evolution where time steps between MCNP are smaller,
and add more and more nuclei as far as the evolution is going on (with
bigger time steps between MCNP runs).
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[bb=0bp 0bp 411bp 507bp,clip,width=6cm]{fig/nuclei_tree}
\par
\end{centering}\par
\protect
\end{figure}](Timg12.gif)
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=16cm]{fig/nuclei_treeS2}
\par
\end{centering}\par
\protect
\end{figure}](Timg14.gif)
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/Th232_1h_initjon}
\par
\end{centering}\par
\protect
\end{figure}](Timg15.gif)
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/Uox_1h_initjon}
\par
\end{centering}\par
\protect
\end{figure}](Timg16.gif)
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/NucleivsT1_2}
\par
\end{centering}\par
\protect
\end{figure}](Timg20.gif)
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=14cm]{fig/NucleivsRecursion}
\par
\end{centering}\par
\protect
\end{figure}](Timg25.gif)
 +
+ 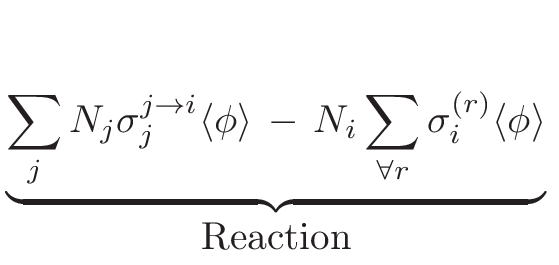
![]() = {N0, N1 ,…, Nn}
is done automatically using a fourth-order Runge-Kutta-type integration
method.
= {N0, N1 ,…, Nn}
is done automatically using a fourth-order Runge-Kutta-type integration
method.
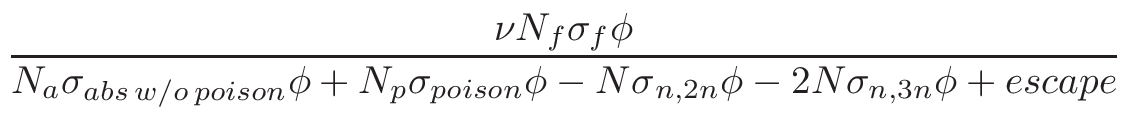
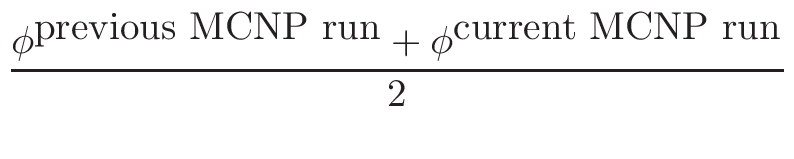
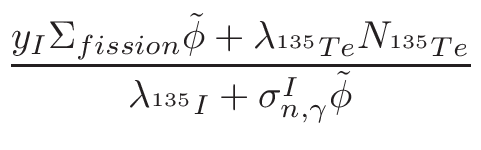
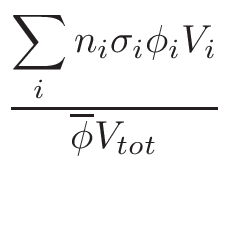
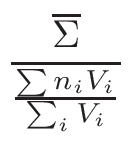 =
= 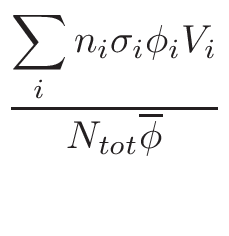 .
.
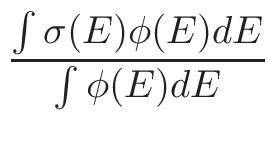
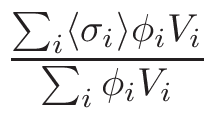 .
In MureGui, one can plot this king of microscopic cross-section by
selecting the ``Micro (spectrum)'' radio widget.
.
In MureGui, one can plot this king of microscopic cross-section by
selecting the ``Micro (spectrum)'' radio widget.
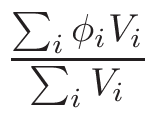
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/NeutronBalanceWin}
\par
\end{centering}\par
\protect
\par
\end{figure}](Timg62.gif)
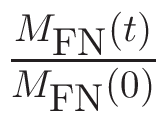
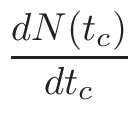 = - A.N(tc)
= - A.N(tc)
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=15cm]{fig/radiotox_Irrad}
\par
\end{centering}\par
\protect
\end{figure}](Timg71.gif)
![\begin{figure}\endgraf
\par
\begin{centering}
\includegraphics[width=14cm]{fig/spatialvar_tab}
\par
\end{centering}\par
\protect
\par
\end{figure}](Timg72.gif)
![]() =
= 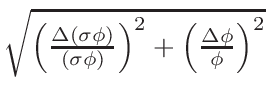 . This is correct only if φ and
(σφ) are not correlated...which
is obviously not the case. Thus only error for keff and fluxes
are really correct.
. This is correct only if φ and
(σφ) are not correlated...which
is obviously not the case. Thus only error for keff and fluxes
are really correct.
![]() on several individual cells
(with an individual flux of φi), we have:
on several individual cells
(with an individual flux of φi), we have:
![]()
![]() of one specific reaction j (linked to the corresponding nucleus)
on several individual cells i, we have:
of one specific reaction j (linked to the corresponding nucleus)
on several individual cells i, we have:
![$ \sqrt{{\sum_{i}\left(N_{j,i}\sigma{}_{j,i}\phi_{i}\right)^{2}\left[\left(\frac...
...gma_{j,i}}\right)^{2}+\left(\frac{\Delta\phi_{i}}{\phi_{i}}\right)^{2}\right]}}$](img87.gif)
![$ \sqrt{{\sum_{j}\sum_{i}\left(Q_{j}N_{j,i}\sigma{}_{j,i}\phi_{i}\right)^{2}\lef...
...gma_{j,i}}\right)^{2}+\left(\frac{\Delta\phi_{i}}{\phi_{i}}\right)^{2}\right]}}$](img89.gif)
![\begin{figure}\endgraf
\begin{centering}
\includegraphics[width=10cm]{fig/NucEmit}
\par
\end{centering}\par
\protect
\end{figure}](Timg91.gif)
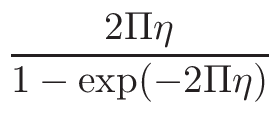 ×W×
×W×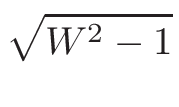 ×
×![]() α, n
α, n![]() reactions (NeutronSpectrum::AddAlphaNSpectra
method), and neutrons from
β-N (NeutronSpectrum::ReadENSDF
method).
reactions (NeutronSpectrum::AddAlphaNSpectra
method), and neutrons from
β-N (NeutronSpectrum::ReadENSDF
method).
![]() -
- ![]()
![]() .sinh
.sinh![]()
![]()
![]() where
a and b are coefficient depending on the nucleus.
where
a and b are coefficient depending on the nucleus.
![]() α, n
α, n![]() Ne
and
18O
Ne
and
18O![]() α, n
α, n![]() Ne. To compute neutron spectra
from these reactions, one needs alpha spectra, stopping power in the
media, cross sections leading to different level of ANe and
oxygen density (for each isotopes). Default values are natural oxygen
density in UOx fuel (
ρ = 10.4g.cm-3).
Ne. To compute neutron spectra
from these reactions, one needs alpha spectra, stopping power in the
media, cross sections leading to different level of ANe and
oxygen density (for each isotopes). Default values are natural oxygen
density in UOx fuel (
ρ = 10.4g.cm-3).
![]() having a
(α, n)
reactions on target i while alpha slowing down on dx
is
pi = Niσidx, where
σi is the
(α, n)
cross section on target i. The probability pi can be
expressed as a function of the variation of energy of the alpha particle
on dx :
pi = Nσ
having a
(α, n)
reactions on target i while alpha slowing down on dx
is
pi = Niσidx, where
σi is the
(α, n)
cross section on target i. The probability pi can be
expressed as a function of the variation of energy of the alpha particle
on dx :
pi = Nσ![]() dE. By integrating the energy
of the alpha particle from it's initial energy to 0:
dE. By integrating the energy
of the alpha particle from it's initial energy to 0:
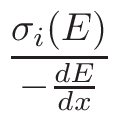 dE
dE

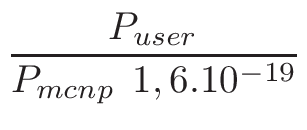 =
=