Interaction des photons gamma VHE avec le CIB

L'influence de la présence de photons de basse énergie (précisément dans la gamme infrarouge) sur la propagation des rayons gamma a été évoquée dès 1962 par Nikishov [210]. Stecker [211] a proposé d'utiliser cette interaction pour sonder le CIB à l'aide des photons gamma de très haute énergie. L'idée de base consiste à étudier un éventuel effet d'absorption dans le spectre suite au processus de création de paires par collisions $\gamma_{gamma}+\gamma_{IR} \rightarrow e^+ + e^-$.

Le phénomène physique est une interaction entre un photon gamma d'énergie $(1+z)E$ et un photon infrarouge d'énergie $(1+z)\epsilon$, où $z$ est le décalage spectral de la source, $E$ et $\epsilon$ les énergies observées à $z=0$. Le seuil énergétique est $E\epsilon\left(1+z\right)^2\left(1-cos\theta\right)>2\left(mc^2\right)^2$ où $\theta$ est l'angle entre les photons et $m$ la masse au repos de l'électron. La section efficace peut être écrite comme [123]:

$$\sigma=1.25\times10^{-25}\left(1-\beta^2\right)\left(2\beta\l... ...\right)ln\left(\frac{1+\beta}{1-\beta}\right)\right) {\rm cm}^2$$

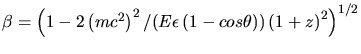avec $\beta=\left(1-2\left(mc^2\right)^2/(E\epsilon\left(1-cos\theta\right))\left(1+z\right)^2\right)^{1/2}$. Si les photons infrarouge ont une densité numérique $n\left(\epsilon\right)d\epsilon~{\rm cm}^{-3}$, la profondeur optique d'atténuation correspondante s'écrit

$$\tau(E)=\frac{c}{H_0}\int_0^{z_s}dz\left(1+z\right)^{1/2}\int... ...silon_t}^{\infty}d\epsilon n(\epsilon)\sigma(E,\epsilon,\theta)$$

avec $\epsilon_t=2(mc^2)^2/(E(1-cos\theta)(1+z)^2)$, $z_s$ le décalage spectral de la source, $c$ la vitesse de la lumière et $H_0$ la constante de Hubble. Dans cette équation, le paramètre de densité $\Omega_0$ a été supposé de l'ordre de l'unité. Le flux résultant est alors atténué d'un facteur $e^{-\tau(E)}$.

La section efficace croît rapidement avec l'énergie du photon cible au-dessus du seuil et décroît ensuite plus lentement après le maximum. La valeur la plus haute est atteinte pour un photon infrarouge de longueur d'onde $\lambda_{IR}\approx \lambda_c \frac{E_{gamma}}{2mc^2}$ où $\lambda_c=h/(mc)$ est la longueur d'onde Compton de l'électron (cf Annexe B).